Gist
Biochemistry explores chemical processes related to living organisms. It is a laboratory-based science combining biology and chemistry. Biochemists study the structure, composition, and chemical reactions of substances in living systems and, in turn, their functions and ways to control them.
Biochemistry studies the chemical processes and substances within living organisms, exploring how molecules interact and contribute to life's functions. It's a multidisciplinary field combining biology and chemistry to understand the molecular basis of life, from cellular processes to the development and function of tissues and organs. Biochemists investigate how molecules like proteins, lipids, and nucleic acids interact and contribute to various biological processes, including metabolism, heredity, and disease.
Summary
Biochemistry, or biological chemistry, is the study of chemical processes within and relating to living organisms. A sub-discipline of both chemistry and biology, biochemistry may be divided into three fields: structural biology, enzymology, and metabolism. Over the last decades of the 20th century, biochemistry has become successful at explaining living processes through these three disciplines. Almost all areas of the life sciences are being uncovered and developed through biochemical methodology and research. Biochemistry focuses on understanding the chemical basis that allows biological molecules to give rise to the processes that occur within living cells and between cells, in turn relating greatly to the understanding of tissues and organs as well as organism structure and function. Biochemistry is closely related to molecular biology, the study of the molecular mechanisms of biological phenomena.
Much of biochemistry deals with the structures, functions, and interactions of biological macromolecules such as proteins, nucleic acids, carbohydrates, and lipids. They provide the structure of cells and perform many of the functions associated with life. The chemistry of the cell also depends upon the reactions of small molecules and ions. These can be inorganic (for example, water and metal ions) or organic (for example, the amino acids, which are used to synthesize proteins). The mechanisms used by cells to harness energy from their environment via chemical reactions are known as metabolism. The findings of biochemistry are applied primarily in medicine, nutrition, and agriculture. In medicine, biochemists investigate the causes and cures of diseases. Nutrition studies how to maintain health and wellness and also the effects of nutritional deficiencies. In agriculture, biochemists investigate soil and fertilizers with the goal of improving crop cultivation, crop storage, and pest control. In recent decades, biochemical principles and methods have been combined with problem-solving approaches from engineering to manipulate living systems in order to produce useful tools for research, industrial processes, and diagnosis and control of disease—the discipline of biotechnology.
Details
Biochemistry is study of the chemical substances and processes that occur in plants, animals, and microorganisms and of the changes they undergo during development and life. It deals with the chemistry of life, and as such it draws on the techniques of analytical, organic, and physical chemistry, as well as those of physiologists concerned with the molecular basis of vital processes.
All chemical changes within the organism—either the degradation of substances, generally to gain necessary energy, or the buildup of complex molecules necessary for life processes—are collectively called metabolism. These chemical changes depend on the action of organic catalysts known as enzymes, and enzymes, in turn, depend for their existence on the genetic apparatus of the cell. It is not surprising, therefore, that biochemistry enters into the investigation of chemical changes in disease, drug action, and other aspects of medicine, as well as in nutrition, genetics, and agriculture.
The term biochemistry is synonymous with two somewhat older terms: physiological chemistry and biological chemistry. Those aspects of biochemistry that deal with the chemistry and function of very large molecules (e.g., proteins and nucleic acids) are often grouped under the term molecular biology. Biochemistry has been known under that term since about 1900. Its origins, however, can be traced much further back; its early history is part of the early history of both physiology and chemistry.
Historical background
The particularly significant past events in biochemistry have been concerned with placing biological phenomena on firm chemical foundations.
Before chemistry could contribute adequately to medicine and agriculture, however, it had to free itself from immediate practical demands in order to become a pure science. This happened in the period from about 1650 to 1780, starting with the work of Robert Boyle and culminating in that of Antoine-Laurent Lavoisier, the father of modern chemistry. Boyle questioned the basis of the chemical theory of his day and taught that the proper object of chemistry was to determine the composition of substances. His contemporary John Mayow observed the fundamental analogy between the respiration of an animal and the burning, or oxidation, of organic matter in air. Then, when Lavoisier carried out his fundamental studies on chemical oxidation, grasping the true nature of the process, he also showed, quantitatively, the similarity between chemical oxidation and the respiratory process.
Photosynthesis was another biological phenomenon that occupied the attention of the chemists of the late 18th century. The demonstration, through the combined work of Joseph Priestley, Jan Ingenhousz, and Jean Senebier, that photosynthesis is essentially the reverse of respiration was a milestone in the development of biochemical thought.
In spite of these early fundamental discoveries, rapid progress in biochemistry had to wait upon the development of structural organic chemistry, one of the great achievements of 19th-century science. A living organism contains many thousands of different chemical compounds. The elucidation of the chemical transformations undergone by these compounds within the living cell is a central problem of biochemistry. Clearly, the determination of the molecular structure of the organic substances present in living cells had to precede the study of the cellular mechanisms, whereby these substances are synthesized and degraded.
There are few sharp boundaries in science, and the boundaries between organic and physical chemistry, on the one hand, and biochemistry, on the other, have always shown much overlap. Biochemistry has borrowed the methods and theories of organic and physical chemistry and applied them to physiological problems. Progress in this path was at first impeded by a stubborn misconception in scientific thinking—the error of supposing that the transformations undergone by matter in the living organism were not subject to the chemical and physical laws that applied to inanimate substances and that consequently these “vital” phenomena could not be described in ordinary chemical or physical terms. Such an attitude was taken by the vitalists, who maintained that natural products formed by living organisms could never be synthesized by ordinary chemical means. The first laboratory synthesis of an organic compound, urea, by Friedrich Wöhler in 1828, was a blow to the vitalists but not a decisive one. They retreated to new lines of defense, arguing that urea was only an excretory substance—a product of breakdown and not of synthesis. The success of the organic chemists in synthesizing many natural products forced further retreats of the vitalists. It is axiomatic in modern biochemistry that the chemical laws that apply to inanimate materials are equally valid within the living cell.
At the same time that progress was being impeded by a misplaced kind of reverence for living phenomena, the practical needs of humans operated to spur the progress of the new science. As organic and physical chemistry erected an imposing body of theory in the 19th century, the needs of the physician, the pharmacist, and the agriculturalist provided an ever-present stimulus for the application of the new discoveries of chemistry to various urgent practical problems.
Two outstanding figures of the 19th century, Justus von Liebig and Louis Pasteur, were particularly responsible for dramatizing the successful application of chemistry to the study of biology. Liebig studied chemistry in Paris and carried back to Germany the inspiration gained by contact with the former students and colleagues of Lavoisier. He established at Giessen a great teaching and research laboratory, one of the first of its kind, which drew students from all over Europe.
Besides putting the study of organic chemistry on a firm basis, Liebig engaged in extensive literary activity, attracting the attention of all scientists to organic chemistry and popularizing it for the layman as well. His classic works, published in the 1840s, had a profound influence on contemporary thought. Liebig described the great chemical cycles in nature. He pointed out that animals would disappear from the face of Earth if it were not for the photosynthesizing plants, since animals require for their nutrition the complex organic compounds that can be synthesized only by plants. The animal excretions and the animal body after death are also converted by a process of decay to simple products that can be re-utilized only by plants.
In contrast with animals, green plants require for their growth only carbon dioxide, water, mineral salts, and sunlight. The minerals must be obtained from the soil, and the fertility of the soil depends on its ability to furnish the plants with these essential nutrients. But the soil is depleted of these materials by the removal of successive crops; hence the need for fertilizers. Liebig pointed out that chemical analysis of plants could serve as a guide to the substances that should be present in fertilizers. Agricultural chemistry as an applied science was thus born.
In his analysis of fermentation, putrefaction, and infectious disease, Liebig was less fortunate. He admitted the similarity of these phenomena but refused to admit that living organisms might function as the causative agents. It remained for Pasteur to clarify that matter. In the 1860s Pasteur proved that various yeasts and bacteria were responsible for “ferments,” substances that caused fermentation and, in some cases, disease. He also demonstrated the usefulness of chemical methods in studying these tiny organisms and was the founder of what came to be called bacteriology.
Later, in 1877, Pasteur’s ferments were designated as enzymes, and, in 1897, German chemist Eduard Buchner clearly showed that fermentation could occur in a press juice of yeast, devoid of living cells. Thus a life process of cells was reduced by analysis to a nonliving system of enzymes. The chemical nature of enzymes remained obscure until 1926, when the first pure crystalline enzyme (urease) was isolated. This enzyme and many others subsequently isolated proved to be proteins, which had already been recognized as high-molecular-weight chains of subunits called amino acids.
The mystery of how minute amounts of dietary substances known as the vitamins prevent diseases such as beriberi, scurvy, and pellagra became clear in 1935, when riboflavin (vitamin B2) was found to be an integral part of an enzyme. Subsequent work has substantiated the concept that many vitamins are essential in the chemical reactions of the cell by virtue of their role in enzymes.
In 1929 the substance adenosine triphosphate (ATP) was isolated from muscle. Subsequent work demonstrated that the production of ATP was associated with respiratory (oxidative) processes in the cell. In 1940 F.A. Lipmann proposed that ATP is the common form of energy exchange in many cells, a concept now thoroughly documented. ATP has been shown also to be a primary energy source for muscular contraction.
The use of radioactive isotopes of chemical elements to trace the pathway of substances in the animal body was initiated in 1935 by two U.S. chemists, Rudolf Schoenheimer and David Rittenberg. That technique provided one of the single most important tools for investigating the complex chemical changes that occur in life processes. At about the same time, other workers localized the sites of metabolic reactions by ingenious technical advances in the studies of organs, tissue slices, cell mixtures, individual cells, and, finally, individual cell constituents, such as nuclei, mitochondria, ribosomes, lysosomes, and membranes.
In 1869 a substance was isolated from the nuclei of pus cells and was called nucleic acid, which later proved to be deoxyribonucleic acid (DNA), but it was not until 1944 that the significance of DNA as genetic material was revealed, when bacterial DNA was shown to change the genetic matter of other bacterial cells. Within a decade of that discovery, the double helix structure of DNA was proposed by Watson and Crick, providing a firm basis for understanding how DNA is involved in cell division and in maintaining genetic characteristics.
Advances have continued since that time, with such landmark events as the first chemical synthesis of a protein, the detailed mapping of the arrangement of atoms in some enzymes, and the elucidation of intricate mechanisms of metabolic regulation, including the molecular action of hormones.
Areas of study
A description of life at the molecular level includes a description of all the complexly interrelated chemical changes that occur within the cell—i.e., the processes known as intermediary metabolism. The processes of growth, reproduction, and heredity, also subjects of the biochemist’s curiosity, are intimately related to intermediary metabolism and cannot be understood independently of it. The properties and capacities exhibited by a complex multicellular organism can be reduced to the properties of the individual cells of that organism, and the behavior of each individual cell can be understood in terms of its chemical structure and the chemical changes occurring within that cell.
Chemical composition of living matter
Every living cell contains, in addition to water and salts or minerals, a large number of organic compounds, substances composed of carbon combined with varying amounts of hydrogen and usually also of oxygen. Nitrogen, phosphorus, and sulfur are likewise common constituents. In general, the bulk of the organic matter of a cell may be classified as (1) protein, (2) carbohydrate, and (3) fat, or lipid. Nucleic acids and various other organic derivatives are also important constituents. Each class contains a great diversity of individual compounds. Many substances that cannot be classified in any of the above categories also occur, though usually not in large amounts.
Proteins are fundamental to life, not only as structural elements (e.g., collagen) and to provide defense (as antibodies) against invading destructive forces but also because the essential biocatalysts are proteins. The chemistry of proteins is based on discoveries made by German chemist Emil Fischer, whose work from 1882 demonstrated that proteins are very large molecules, or polymers, built up of about 24 amino acids. Proteins may vary in size from small—insulin with a molecular weight of 5,700 (based on the weight of a hydrogen atom as 1)—to very large—molecules with molecular weights of more than 1,000,000. The first complete amino acid sequence was determined for the insulin molecule in the 1950s.
By 1963 the chain of amino acids in the protein enzyme ribonuclease (molecular weight 12,700) had also been determined, aided by the powerful physical techniques of X-ray-diffraction analysis. In the 1960s, Nobel Prize winners Sir John Cowdery Kendrew and Max Ferdinand Perutz, utilizing X-ray studies, constructed detailed atomic models of the proteins hemoglobin and myoglobin (the respiratory pigment in muscle), which were later confirmed by sophisticated chemical studies. The abiding interest of biochemists in the structure of proteins rests on the fact that the arrangement of chemical groups in space yields important clues regarding the biological activity of molecules.
Carbohydrates include such substances as sugars, starch, and cellulose. The second quarter of the 20th century witnessed a striking advance in the knowledge of how living cells handle small molecules, including carbohydrates. The metabolism of carbohydrates became clarified during this period, and elaborate pathways of carbohydrate breakdown and subsequent storage and utilization were gradually outlined in terms of cycles (e.g., the Embden–Meyerhof glycolytic cycle and the Krebs cycle). The involvement of carbohydrates in respiration and muscle contraction was well worked out by the 1950s.
Fats, or lipids, constitute a heterogeneous group of organic chemicals that can be extracted from biological material by nonpolar solvents such as ethanol, ether, and benzene. The classic work concerning the formation of body fat from carbohydrates was accomplished during the early 1850s. Those studies, and later confirmatory evidence, have shown that the conversion of carbohydrate to fat occurs continuously in the body. The liver is the main site of fat metabolism. Fat absorption in the intestine was studied as early as the 1930s. The control of fat absorption is known to depend upon a combination action of secretions of the pancreas and bile salts. Abnormalities of fat metabolism, which result in disorders such as obesity and rare clinical conditions, are the subject of much biochemical research. Equally interesting to biochemists is the association between high levels of fat in the blood and the occurrence of arteriosclerosis (“hardening” of the arteries).
Nucleic acids are large, complex compounds of very high molecular weight present in the cells of all organisms and in viruses. They are of great importance in the synthesis of proteins and in the transmission of hereditary information from one generation to the next. Originally discovered as constituents of cell nuclei (hence their name), it was assumed for many years after their isolation in 1869 that they were found nowhere else. This assumption was not challenged seriously until the 1940s, when it was determined that two kinds of nucleic acid exist: DNA, in the nuclei of all cells and in some viruses; and ribonucleic acid (RNA), in the cytoplasm of all cells and in most viruses.
The profound biological significance of nucleic acids came gradually to light during the 1940s and 1950s. Attention turned to the mechanism by which protein synthesis and genetic transmission was controlled by nucleic acids (see below Genes). During the 1960s, experiments were aimed at refinements of the genetic code. Promising attempts were made during the late 1960s and early 1970s to accomplish duplication of the molecules of nucleic acids outside the cell—i.e., in the laboratory. By the mid-1980s genetic engineering techniques had accomplished, among other things, in vitro fertilization and the recombination of DNA (so-called gene splicing).
Nutrition
Biochemists have long been interested in the chemical composition of the food of animals. All animals require organic material in their diet, in addition to water and minerals. This organic matter must be sufficient in quantity to satisfy the caloric, or energy, requirements of the animals. Within certain limits, carbohydrate, fat, and protein may be used interchangeably for this purpose. In addition, however, animals have nutritional requirements for specific organic compounds. Certain essential fatty acids, about ten different amino acids (the so-called essential amino acids), and vitamins are required by many higher animals. The nutritional requirements of various species are similar but not necessarily identical; thus man and the guinea pig require vitamin C, or ascorbic acid, whereas the rat does not.
That plants differ from animals in requiring no preformed organic material was appreciated soon after the plant studies of the late 1700s. The ability of green plants to make all their cellular material from simple substances—carbon dioxide, water, salts, and a source of nitrogen such as ammonia or nitrate—was termed photosynthesis. As the name implies, light is required as an energy source, and it is generally furnished by sunlight. The process itself is primarily concerned with the manufacture of carbohydrate, from which fat can be made by animals that eat plant carbohydrates. Protein can also be formed from carbohydrate, provided ammonia is furnished.
In spite of the large apparent differences in nutritional requirements of plants and animals, the patterns of chemical change within the cell are the same. The plant manufactures all the materials it needs, but these materials are essentially similar to those that the animal cell uses and are often handled in the same way once they are formed. Plants could not furnish animals with their nutritional requirements if the cellular constituents in the two forms were not basically similar.
Digestion
The organic food of animals, including humans, consists in part of large molecules. In the digestive tracts of higher animals, these molecules are hydrolyzed, or broken down, to their component building blocks. Proteins are converted to mixtures of amino acids, and polysaccharides are converted to monosaccharides. In general, all living forms use the same small molecules, but many of the large complex molecules are different in each species. An animal, therefore, cannot use the protein of a plant or of another animal directly but must first break it down to amino acids and then recombine the amino acids into its own characteristic proteins. The hydrolysis of food material is necessary also to convert solid material into soluble substances suitable for absorption. The liquefaction of stomach contents aroused the early interest of observers, long before the birth of modern chemistry, and the hydrolytic enzymes secreted into the digestive tract were among the first enzymes to be studied in detail. Pepsin and trypsin, the proteolytic enzymes of gastric and pancreatic juice, respectively, continue to be intensively investigated.
The products of enzymatic action on the food of an animal are absorbed through the walls of the intestines and distributed to the body by blood and lymph. In organisms without digestive tracts, substances must also be absorbed in some way from the environment. In some instances simple diffusion appears to be sufficient to explain the transfer of a substance across a cell membrane. In other cases, however (e.g., in the case of the transfer of glucose from the lumen of the intestine to the blood), transfer occurs against a concentration gradient. That is, the glucose may move from a place of lower concentration to a place of higher concentration.
In the case of the secretion of hydrochloric acid into gastric juice, it has been shown that active secretion is dependent on an adequate oxygen supply (i.e., on the respiratory metabolism of the tissue), and the same holds for absorption of salts by plant roots. The energy released during the tissue oxidation must be harnessed in some way to provide the energy necessary for the absorption or secretion. This harnessing is achieved by a special chemical coupling system. The elucidation of the nature of such coupling systems has been an objective of the biochemist.
Blood
One of the animal tissues that has always excited special curiosity is blood. Blood has been investigated intensively from the early days of biochemistry, and its chemical composition is known with greater accuracy and in more detail than that of any other tissue in the body. The physician takes blood samples to determine such things as the sugar content, the urea content, or the inorganic-ion composition of the blood, since these show characteristic changes in disease.
The blood pigment hemoglobin has been intensively studied. Hemoglobin is confined within the blood corpuscles and carries oxygen from the lungs to the tissues. It combines with oxygen in the lungs, where the oxygen concentration is high, and releases the oxygen in the tissues, where the oxygen concentration is low. The hemoglobins of higher animals are related but not identical. In invertebrates, other pigments may take the place and function of hemoglobin. The comparative study of these compounds constitutes a fascinating chapter in biochemical investigation.
The proteins of blood plasma also have been extensively investigated. The gamma-globulin fraction of the plasma proteins contains the antibodies of the blood and is of practical value as an immunizing agent. An animal develops resistance to disease largely by antibody production. Antibodies are proteins with the ability to combine with an antigen (i.e., an agent that induces their formation). When this agent is a component of a disease-causing bacterium, the antibody can protect an organism from infection by that bacterium. The chemical study of antigens and antibodies and their interrelationship is known as immunochemistry.
Metabolism and hormones
The cell is the site of a constant, complex, and orderly set of chemical changes collectively called metabolism. Metabolism is associated with a release of heat. The heat released is the same as that obtained if the same chemical change is brought about outside the living organism. This confirms the fact that the laws of thermodynamics apply to living systems just as they apply to the inanimate world. The pattern of chemical change in a living cell, however, is distinctive and different from anything encountered in nonliving systems. This difference does not mean that any chemical laws are invalidated. It instead reflects the extraordinary complexity of the interrelations of cellular reactions.
Hormones, which may be regarded as regulators of metabolism, are investigated at three levels, to determine (1) their physiological effects, (2) their chemical structure, and (3) the chemical mechanisms whereby they operate. The study of the physiological effects of hormones is properly regarded as the province of the physiologist. Such investigations obviously had to precede the more analytical chemical studies. The chemical structures of thyroxine and adrenaline are known. The chemistry of the gender and adrenal hormones, which are steroids, has also been thoroughly investigated. The hormones of the pancreas—insulin and glucagon—and the hormones of the hypophysis (pituitary gland) are peptides (i.e., compounds composed of chains of amino acids). The structures of most of these hormones has been determined. The chemical structures of the plant hormones, auxin and gibberellic acid, which act as growth-controlling agents in plants, are also known.
The first and second phases of the hormone problem thus have been well, though not completely, explored, but the third phase is still in its infancy. It seems likely that different hormones exert their effects in different ways. Some may act by affecting the permeability of membranes; others appear to control the synthesis of certain enzymes. Evidently some hormones also control the activity of certain genes.
Genes
Genetic studies have shown that the hereditary characteristics of a species are maintained and transmitted by the self-duplicating units known as genes, which are composed of nucleic acids and located in the chromosomes of the nucleus. One of the most fascinating chapters in the history of the biological sciences contains the story of the elucidation, in the mid-20th century, of the chemical structure of the genes, their mode of self-duplication, and the manner in which the DNA of the nucleus causes the synthesis of RNA, which, among its other activities, causes the synthesis of protein. Thus, the capacity of a protein to behave as an enzyme is determined by the chemical constitution of the gene (DNA) that directs the synthesis of the protein. The relationship of genes to enzymes has been demonstrated in several ways. The first successful experiments, devised by the Nobel Prize winners George W. Beadle and Edward L. Tatum, involved the bread mold Neurospora crassa; the two men were able to collect a variety of strains that differed from the parent strain in nutritional requirements. Such strains had undergone a mutation (change) in the genetic makeup of the parent strain. The mutant strains required a particular amino acid not required for growth by the parent strain. It was then shown that such a mutant had lost an enzyme essential for the synthesis of the amino acid in question. The subsequent development of techniques for the isolation of mutants with specific nutritional requirements led to a special procedure for studying intermediary metabolism.
Evolution and origin of life
The exploration of space beginning in the mid-20th century intensified speculation about the possibility of life on other planets. At the same time, man was beginning to understand some of the intimate chemical mechanisms used for the transmission of hereditary characteristics. It was possible, by studying protein structure in different species, to see how the amino acid sequences of functional proteins (e.g., hemoglobin and cytochrome) have been altered during phylogeny (the development of species). It was natural, therefore, that biochemists should look upon the problem of the origin of life as a practical one. The synthesis of a living cell from inanimate material was not regarded as an impossible task for the future.
Applied biochemistry
An early objective in biochemistry was to provide analytical methods for the determination of various blood constituents because it was felt that abnormal levels might indicate the presence of metabolic diseases. The clinical chemistry laboratory now has become a major investigative arm of the physician in the diagnosis and treatment of disease and is an indispensable unit of every hospital. Some of the older analytical methods directed toward diagnosis of common diseases are still the most commonly used—for example, tests for determining the levels of blood glucose, in diabetes; urea, in kidney disease; uric acid, in gout; and bilirubin, in liver and gallbladder disease. With development of the knowledge of enzymes, determination of certain enzymes in blood plasma has assumed diagnostic value, such as alkaline phosphatase, in bone and liver disease; acid phosphatase, in prostatic cancer; amylase, in pancreatitis; and lactate dehydrogenase and transaminase, in cardiac infarct. Electrophoresis of plasma proteins is commonly employed to aid in the diagnosis of various liver diseases and forms of cancer. Both electrophoresis and ultracentrifugation of serum constituents (lipoproteins) are used increasingly in the diagnosis and examination of therapy of atherosclerosis and heart disease. Many specialized and sophisticated methods have been introduced, and machines have been developed for the simultaneous automated analysis of many different blood constituents in order to cope with increasing medical needs.
Analytical biochemical methods have also been applied in the food industry to develop crops superior in nutritive value and capable of retaining nutrients during the processing and preservation of food. Research in this area is directed particularly to preserving vitamins as well as color and taste, all of which may suffer loss if oxidative enzymes remain in the preserved food. Tests for enzymes are used for monitoring various stages in food processing.
Biochemical techniques have been fundamental in the development of new drugs. The testing of potentially useful drugs includes studies on experimental animals and man to observe the desired effects and also to detect possible toxic manifestations; such studies depend heavily on many of the clinical biochemistry techniques already described. Although many of the commonly used drugs have been developed on a rather empirical (trial-and-error) basis, an increasing number of therapeutic agents have been designed specifically as enzyme inhibitors to interfere with the metabolism of a host or invasive agent. Biochemical advances in the knowledge of the action of natural hormones and antibiotics promise to aid further in the development of specific pharmaceuticals.
Methods in biochemistry
Like other sciences, biochemistry aims at quantifying, or measuring, results, sometimes with sophisticated instrumentation. The earliest approach to a study of the events in a living organism was an analysis of the materials entering an organism (foods, oxygen) and those leaving (excretion products, carbon dioxide). This is still the basis of so-called balance experiments conducted on animals, in which, for example, both foods and excreta are thoroughly analyzed. For this purpose many chemical methods involving specific color reactions have been developed, requiring spectrum-analyzing instruments (spectrophotometers) for quantitative measurement. Gasometric techniques are those commonly used for measurements of oxygen and carbon dioxide, yielding respiratory quotients (the ratio of carbon dioxide to oxygen). Somewhat more detail has been gained by determining the quantities of substances entering and leaving a given organ and also by incubating slices of a tissue in a physiological medium outside the body and analyzing the changes that occur in the medium. Because these techniques yield an overall picture of metabolic capacities, it became necessary to disrupt cellular structure (homogenization) and to isolate the individual parts of the cell—nuclei, mitochondria, lysosomes, ribosomes, membranes—and finally the various enzymes and discrete chemical substances of the cell in an attempt to understand the chemistry of life more fully.
Centrifugation and electrophoresis
An important tool in biochemical research is the centrifuge, which through rapid spinning imposes high centrifugal forces on suspended particles, or even molecules in solution, and causes separations of such matter on the basis of differences in weight. Thus, red cells may be separated from plasma of blood, nuclei from mitochondria in cell homogenates, and one protein from another in complex mixtures. Proteins are separated by ultracentrifugation—very high speed spinning; with appropriate photography of the protein layers as they form in the centrifugal field, it is possible to determine the molecular weights of proteins.
Another property of biological molecules that has been exploited for separation and analysis is their electrical charge. Amino acids and proteins possess net positive or negative charges according to the acidity of the solution in which they are dissolved. In an electric field, such molecules adopt different rates of migration toward positively (anode) or negatively (cathode) charged poles and permit separation. Such separations can be effected in solutions or when the proteins saturate a stationary medium such as cellulose (filter paper), starch, or acrylamide gels. By appropriate color reactions of the proteins and scanning of color intensities, a number of proteins in a mixture may be measured. Separate proteins may be isolated and identified by electrophoresis, and the purity of a given protein may be determined. (Electrophoresis of human hemoglobin revealed the abnormal hemoglobin in sickle-cell anemia, the first definitive example of a “molecular disease.”)
Chromatography and isotopes
The different solubilities of substances in aqueous and organic solvents provide another basis for analysis. In its earlier form, a separation was conducted in complex apparatus by partition of substances in various solvents. A simplified form of the same principle evolved as ‘‘paper chromatography,” in which small amounts of substances could be separated on filter paper and identified by appropriate color reactions. In contrast to electrophoresis, this method has been applied to a wide variety of biological compounds and has contributed enormously to research in biochemistry.
The general principle has been extended from filter paper strips to columns of other relatively inert media, permitting larger scale separation and identification of closely related biological substances. Particularly noteworthy has been the separation of amino acids by chromatography in columns of ion-exchange resins, permitting the determination of exact amino acid composition of proteins. Following such determination, other techniques of organic chemistry have been used to elucidate the actual sequence of amino acids in complex proteins. Another technique of column chromatography is based on the relative rates of penetration of molecules into beads of a complex carbohydrate according to size of the molecules. Larger molecules are excluded relative to smaller molecules and emerge first from a column of such beads. This technique not only permits separation of biological substances but also provides estimates of molecular weights.
Perhaps the single most important technique in unraveling the complexities of metabolism has been the use of isotopes (heavy or radioactive elements) in labeling biological compounds and “tracing” their fate in metabolism. Measurement of the isotope-labeled compounds has required considerable technology in mass spectroscopy and radioactive detection devices.
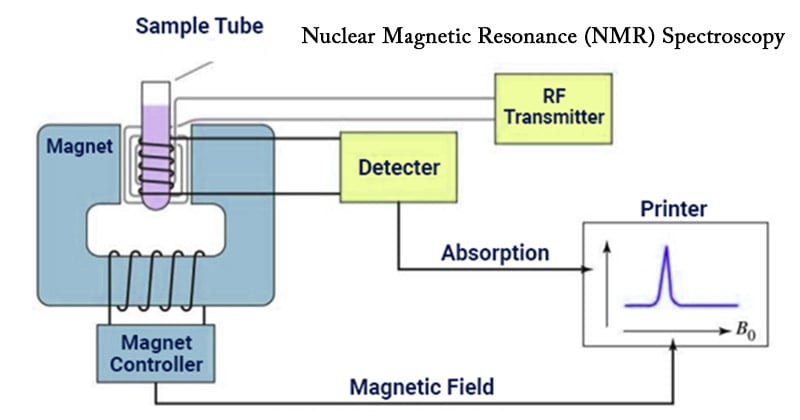
A variety of other physical techniques, such as nuclear magnetic resonance, electron spin spectroscopy, circular dichroism, and X-ray crystallography, have become prominent tools in revealing the relation of chemical structure to biological function.
Additional Information
Biochemistry is the study of the chemicals that make up life and how they behave. It seeks to explain how inanimate chemicals like carbohydrates and proteins can give rise to living organisms.
Biochemistry as a scientific discipline began in the 1700s and 1800s, with early studies of phenomena like fermentation and the discovery of the first enzyme. However, it blossomed in the 20th century, thanks in part to new techniques like X-ray crystallography that allowed biochemists to study the precise three-dimensional structures of molecules.
Perhaps the most famous biochemical molecule is deoxyribonucleic acid or DNA, the material that carries our genes. The structure of DNA was discovered in 1953 after a frantic (and at times disreputable) race. Famously, DNA is a double helix, made up of two strands that coil around each other. Each strand carries a sequence of “letters”, which are the basis of genes.
In the wake of this discovery, biochemists like Francis Crick realised that the information on DNA is used to make proteins, which are long chains of smaller molecules called amino acids. Proteins are the workhorses of living cells, doing everything from digesting food to pushing waste out of the cell. The long chains fold up into remarkably intricate structures, which are crucial to the proteins’ function.
However, before proteins can be made the information from DNA is first copied onto a third kind of molecule called RNA (ribonucleic acid), which is similar to DNA. RNA can also act as an enzyme, as proteins do. Its ability to perform so many tasks has led some biochemists to suggest that it played a key role in the origin of life on Earth, before DNA and protein arose.
Besides genetics, a second key area of biochemistry is metabolism: the processes by which organisms extract energy from their environment (for instance from food) and use it to move and build their bodies. Metabolism involves elaborate sequences of chemical reactions, some of which are cyclic so the original chemicals are recreated at the end. Complex chemicals are broken down into simpler ones to provide energy, and that energy is used to build new chemicals that the organism can use. Different organisms can have radically different metabolisms.
Biochemistry has also revealed that living cells have structural molecules. Some form the walls and membranes that surround cells and hold them together, while others link up into a kind of scaffolding called the cytoskeleton.
Other biochemical molecules are remarkable feats of evolutionary engineering. There are molecular motors and even rotating axles.
Biochemists are still discovering new things about natural organisms (although reports that some organisms can incorporate math into their DNA appear to be false). They have also started designing new biochemistries, for example adding new letters to the DNA “alphabet” or swapping out some of the amino acids used to make proteins. This synthetic biology may lead to new medicines and other biotechnologies, as well as shedding light on the nature of life.