Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#276 Help Me ! » one thousand rooms » 2007-11-24 05:00:29
- tony123
- Replies: 3
There are one thousand rooms in the sultan's palace. In each room there is a switch that switches all the lamps in the room on or off. When the lamps were on in each room and the sultan was bored, he walked through all his rooms one by one and repeated his walk again and again, always starting with the first room. During the first walk, he turned all the switches. The second time he turned the switch in every second room. The third time he turned the switch in every third room, and so on. (He turned the light on if it was off, and he turned it off if it was on). When he had walked through his room 500 times, he got tired of the game and decided to go to bed. He needed a room in which the lights were off. Which rooms did he have to choose from?
#277 Help Me ! » solve » 2007-11-22 20:20:45
- tony123
- Replies: 4
#278 Help Me ! » simplify » 2007-11-19 09:12:59
- tony123
- Replies: 9
simplify
#279 Help Me ! » ABCD is a cyclic quadrilateral » 2007-11-18 23:06:53
- tony123
- Replies: 1
ABCD is a cyclic quadrilateral, with side
AD= d
where d is the diameter of the circle. AB= a
BC= a
and CD= b
If a, b and d are integers a ≠ b
(a)prove that d cannot be a prime number
.
(b)determine the minimum value of d.
#280 Help Me ! » solve » 2007-11-18 09:19:25
- tony123
- Replies: 5

#281 Help Me ! » Determine » 2007-11-16 22:04:55
- tony123
- Replies: 1
Determine all positive integers a and b such that
divides
#282 Help Me ! » Determine the integer n with the properties » 2007-11-16 21:59:20
- tony123
- Replies: 3
Determine the integer n with the properties :
1.)n is a prime less than 6000
2.)The number formed by the last two digits of n is < 10
3.)If the decimal digits of n are reversed to obtain N , then N - n = 999
#283 Help Me ! » collinear points » 2007-11-16 21:40:48
- tony123
- Replies: 0
A, B, C, D are collinear points in this order. Draw the regular triangles ABE and CDF on one side of the line. Let G denote the intersection of the circles ACE and BDF on the same side of the line ABCD. Prove that < AGD=120 °.
#284 Help Me ! » How many » 2007-11-16 10:19:49
- tony123
- Replies: 2
How many five-digit numbers are there in which the sum of the digits equals the sum of the square of the digits?
#285 Re: Help Me ! » hexagon » 2007-11-16 09:28:41
equilateral triangles at two opposite ends
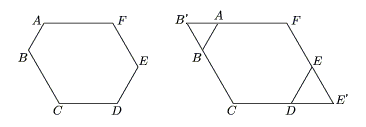
#286 Help Me ! » divisible by 10 000. » 2007-11-16 09:13:56
- tony123
- Replies: 2
Prove that if the difference of the integers a, b is divisible by 100, then
is divisible by 10 000.
#287 Help Me ! » solve log » 2007-11-16 05:59:35
- tony123
- Replies: 1
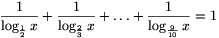
#288 Help Me ! » minimum value » 2007-11-16 05:45:08
- tony123
- Replies: 2
Find the minimum value of the function
.#289 Help Me ! » Evaluate the sum » 2007-11-15 21:19:23
- tony123
- Replies: 1
Evaluate the sum
.
#290 Help Me ! » ratio of two integers: » 2007-11-15 10:06:58
- tony123
- Replies: 1
Express the following sum as a ratio of two integers:
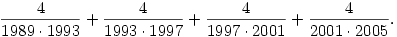
#291 Help Me ! » Evaluate » 2007-11-15 05:47:12
- tony123
- Replies: 1
Evaluate cot x, given that
?#292 Help Me ! » prove » 2007-11-13 05:01:55
- tony123
- Replies: 1
sin 25°.sin 35°.sin 60°.sin 85°=sin 20°.sin 40°.sin 75°.sin 80°.
#293 Help Me ! » determine the angles of these two triangles. » 2007-11-11 08:04:59
- tony123
- Replies: 0
In a triangle ABC, AC=BC. There is given a point P on side AB such that ACP=30o. In addition, point Q outside the triangle satisfies
<CPQ=<CPA+<APQ=78°.
Given that all angles of triangles ABC and QPB, measured in degrees, are integers, determine the angles of these two triangles.
#294 Help Me ! » solve in R » 2007-11-11 07:03:23
- tony123
- Replies: 16
#295 Help Me ! » hexagon » 2007-11-08 09:23:32
- tony123
- Replies: 7
Each interior angle of the hexagon in the figure is 120°. Prove that
AB + FA = CD + DE.
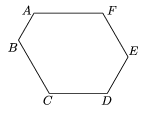
#296 Help Me ! » How far is the turning point K » 2007-11-08 05:13:08
- tony123
- Replies: 4
The sum of the non-negative real numbers
is 2 and. Find the largest and smallest possible values of#297 Help Me ! » How many solutions » 2007-11-05 10:47:29
- tony123
- Replies: 1
How many solutions does the equation
have in the interval?#298 Help Me ! » X and Y are interior points » 2007-11-05 05:58:38
- tony123
- Replies: 0
X and Y are interior points of the square ABCD such that <XAY= <XCY= 45°. Determine the length XY in terms of the lengths BX and DY.
#299 Help Me ! » solve » 2007-11-03 09:25:04
- tony123
- Replies: 1
#300 Help Me ! » find a,b,c,d » 2007-11-03 09:11:02
- tony123
- Replies: 1
find a,b,c,d for all x satisfay equation