Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#26 Re: Help Me ! » How would i start re learning mathematics ? » 2022-01-11 04:58:35
Hello dummy39,
I second Bob's comment. MIF is an exceptionally eloquent and extensively documented website for anyone wishing to cover the essentials(and even more)!
#27 Re: Help Me ! » Mixed fractions explanation step by step » 2022-01-08 06:48:24
Hello suliko60,
This tool available at Calculator Soup appears to fit the bill.
#28 Re: Help Me ! » Angles of a Parallelogram » 2022-01-06 11:10:19
Hello guys,
I know this is a little off-topic, but as a response to CurlyBracket's Latin phrase question, a Latin phrase I find most shrewd is:
Amicus certus in re incerta cernitur.
— Ennius
It means: One's friends are known in the hour of need. Indeed, an adage that will stay true for eternity.
#29 Re: Introductions » New Year, New Sign Up! » 2022-01-06 02:52:31
Hi CurlyBracket,
Glad to see newcomers. Welcome to the forum!
#30 Re: Introductions » Hello » 2022-01-02 16:43:14
Hello Mathman2022,
Welcome to MIF!
#31 Re: Help Me ! » What do you do in your freetime? » 2021-12-28 03:16:03
Hello Henry17,
Attempt to continuously hone my skills in mathematics, programming, and more broadly problem solving.
#32 Re: Help Me ! » How can I prove this equation » 2021-12-28 03:14:08
I know this probably isn't the intended way of solving it, but you could just solve the quartic with some simple completing the square, and hence prove the expression on the right.
#33 Re: Help Me ! » write a function of this graph : » 2021-12-25 18:43:53
Hello,
See:
#34 Re: Help Me ! » write a function of this graph : » 2021-12-19 14:00:33
D alludes to the distance between the horizontal asymptote and the y-value of the graph.
The function, as noted in the answer, is exponential, so the equation is of an exponential form. The
Because D represents the distance between the horizontal asymptote(that is, ) and the y-value of the function, D is equal to 4-y.
#35 Re: Help Me ! » rate of growth/decay in exponential function » 2021-12-16 11:42:47
Mathegocart wrote:How so? As zetafunc mentions above, the function
is equivalent to the function you mentioned, and the equation is continuous.can you please see this YouTube link it talked about it and it said there is differences :-
https://www.youtube.com/watch?v=VmxESGI4zdA&t=18s
also see this sheet pls :
As stated, one can be converted into the other. So it is continuous. The current form isn't, but it can be converted into an equivalent continuous form.
#36 Re: Help Me ! » rate of growth/decay in exponential function » 2021-12-15 17:44:42
Mathegocart wrote:Yes, the equation does represent continuous growth. As noted, you can convert that equation into the form of the continuous standard equation
with the substitution mentioned above.I think it's not right, because I found the answer today
the form model without e and k like this :
is called non-continuous exponential models functions
because in case of increasing (a>1) while in case of model contain e, and k, if k is positive it's increasing continuously rate (because any positive number is acceptable and in case of base a there is numbers less then 1 are positive but not included)
and in case of decreasing (0<a<1) while in case of e, and k, here k is has to be negative <0 so it's continuously decreasing rateso now
its growth rate is not continuous,
am I right?
by the way I learned this today from a YouTube channel but I still don't understand why we can't called the base a a continuous if it's >1
I knew because it doesn't included the numbers that less than 1 and bigger than 0
but why? why this is a reasons that we can't call it continuously, what is meaning continuously in this case anyway? because every graph I draw in form of non-continuous exponential models I see them clearly in my naked eyes that they are continuous, I draw these random examples as in example I see them all goes beyond without end
How so? As zetafunc mentions above, the function
is equivalent to the function you mentioned, and the equation is continuous.#37 Re: Help Me ! » rate of growth/decay in exponential function » 2021-12-15 13:03:13
Mathegocart wrote:Hannibal lecter wrote:yes sorry I'm trying to use the site in better ways
so branch 7,8 continues growth of rate
andwhat about branch 5,6 :
can we say it's continuous growth of rate too?No, because . Continuous growth is modeled with the equation
, where is the ending value, is the initial value, is Euler's constant, is the continuous growth rate, and is the time that has passed.Diregard what I wrote above; as zetafunc helpfully noted,
could be represented as .I'm talking about e and k and exponential form I'm talking about this form :
is the growth rate 7% here is called continuous or we can't call it this
Yes, the equation does represent continuous growth. As noted, you can convert that equation into the form of the continuous standard equation
with the substitution mentioned above.#38 Re: Help Me ! » rate of growth/decay in exponential function » 2021-12-15 09:36:18
Mathegocart wrote:No, because continuous growth is modeled with the equation
, where is the ending value, is the initial value, is Euler's constant, is the continuous growth rate, and is the time that has passed.What's stopping you from taking k = log(1.07)?
I was a little fatigued when I wrote that up; that's true.
#39 Re: Help Me ! » rate of growth/decay in exponential function » 2021-12-14 12:04:21
Bob wrote:yes what is that gradient value of -k?
I hope I have answered all your questions here. I found it difficult to keep scrolling back to two separate posts. I would rather you kept them separate, thanks.
Bob
yes sorry I'm trying to use the site in better ways
so branch 7,8 continues growth of rate
andwhat about branch 5,6 :
can we say it's continuous growth of rate too?
No, because . Continuous growth is modeled with the equation
, where is the ending value, is the initial value, is Euler's constant, is the continuous growth rate, and is the time that has passed.Diregard what I wrote above; as zetafunc helpfully noted,
could be represented as .#40 Re: Help Me ! » why subtract this kinky number is equal 1 » 2021-12-12 15:27:04
This inaccuracy derives from how computers represent real numbers, after all, computers handle and tinker around with binary numbers and mathematics, and it is impossible to represent all real numbers in binary, and this leads to a plethora of idiosyncracies; another one is that tan(pi/2) will not yield infinity not result in an overflow in the typical floating-point representations; if you type tan(pi/2) into a humble calculator that is not programmed with these cases in mind, the result will be
. In particular, there does not seem to be a high level of precision in these calculators that are specifically designed with general-purpose calculations.#41 Guestbook » I'm Back! (Again) » 2021-11-27 17:37:30
- Mathegocart
- Replies: 3
Hello all MIF members,
Yes, it is me, the one and only Mathgogocart(reformed to Mathegocart a while back.) Anyways, after a lengthy and laborious process of managing, perusing, and tackling a pugnacious set of problems and issues regarding my academic life and personal life, I'm back. Also, I'm studying linear algebra, abstract algebra, and p-adic numbers, and attempting to hone my skills at them. In the intervening period, I also added to my repertoire some HTML, CSS, and Javascript skills, most notably in the form of analyzing the plethora of CSS attributes and selectors, along with developing my own React-based websites. I also decided to finally sit down and learn some LaTeX(as the late Bobbym requested me too a while back.) Although I'm certainly no expert at the markup language, I've added it to my mathematical repertoire.
I will most probably assist in combatting the surge of problems that flow in the "Help Me!" section with my novel tools in my rhetorical mathematical toolbox.
Thanks,
Mathegocart.
#42 Re: Help Me ! » Business Application » 2021-05-09 12:54:15
A roofing contractor purchases a shingle delivery truck with a shingle
elevator for $42,000. The vehicle requires an average expenditure of $9.50 per hour for fuel and maintenance, and the operator is paid $11.50 per hour.(a) Write a linear equation giving the total cost C of operating this equipment for t hours. (Include the purchase cost of the equipment.)
I must add 9.50 + 11.50 to get 21
I then multiply 21 times t.
I finally add 21t to 42,000.
My equation is C(t) = 42,000 + 21t.
Is this correct?
(b) Assuming that customers are charged $45 per hour of machine use, write an equation for the revenue R
obtained from t hours of use.I know the revenue formula is
Revenue = Quantity × Price.I say the formula is R = 45t.
Is this right?
(c) Use the formula for profit P = R − C to write an equation for the profit obtained from t hours of use.
If R = 45t, and C = 42,000, I say the equation needed is P = 45t - 42,000.
Is this right?
(d) Use the result of part (c) to find the break-even point—that is, the number of hours this equipment
must be used to yield a profit of 0 dollars.I am not too sure about part (d). What is break-even in the business world?
Thanks.
(a) You betcha.
(b) Yup.
(c) Well, there might be a typo here. R = 45t and C = (21t + 42000). So R - C = 24t - 42,000.
(d) Find the number of hours(t) that it takes for revenue to meet costs; i.e, when does R - C = 0?
#43 Re: Help Me ! » I'm back - How do I hide a reply? » 2021-05-09 12:47:41
Mathegocart wrote:mathland wrote:Ok. I will play with this later on.
I recommend the site "postimage" instead. Less of nouveau-web math and clutter, and it loads faster.
After signing up with postimage, what is the next step?
Again, it is not necessary to sign up for postimage if you just want to post a picture.
Click "choose image" here:
After submitting an image, you will be led to a page containg links of the image.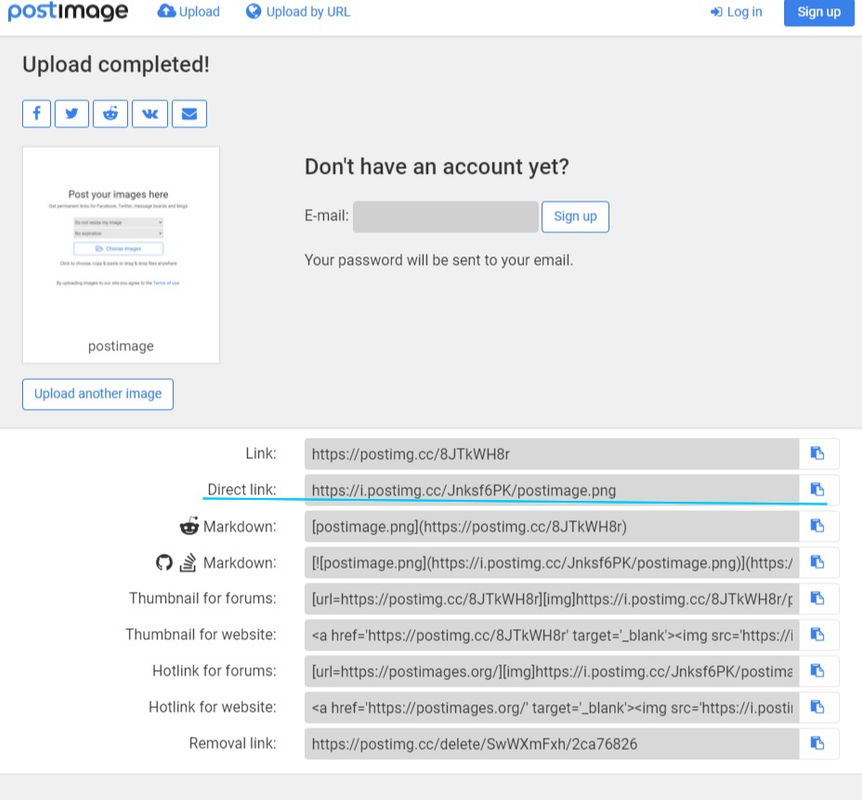
Then copy and paste the "Direct Link" URL here:
[img]DIRECTLINK[/img]
#44 Re: Help Me ! » Testing For Functions Represented Algebraically » 2021-05-09 04:17:07
Yes and yes.
#45 Re: Help Me ! » Chain Rule » 2021-05-09 04:16:07
zetafunc wrote:You can calculate what each of those four terms are.
Sorry but I was not able to figure it out. Boy, do I miss yahoo answers.
Just take the derivative of each of those functions - it's the chain rule, expressed graphically.
#46 Re: Help Me ! » I'm back - How do I hide a reply? » 2021-05-09 04:11:30
David wrote:Sign up on imgur and once you upload an image, to embed look for the BBcode.
sample here:[img]https://i.imgur.com/iW6bGpj.png[/img]https://i.imgur.com/5bUJoIJ.png
Ok. I will play with this later on.
I recommend the site "postimage" instead. Less of nouveau-web math and clutter, and it loads faster.
#47 Re: Help Me ! » Minimum & Maximum » 2021-05-05 16:18:08
zetafunc wrote:You'd need to:
-Differentiate w(x) with respect to x, to obtain an expression for w'(x)
-Find the values of x for which w'(x) = 0
-Substitute these values of x into your equation for w''(x) to determine which values of x correspond to a minimum and which correspond to a maximumOk. Now, by w"(x) you mean the second derivative. Yes?
That's what it means, yes.
#48 Re: Help Me ! » Equation of a Circle » 2021-05-05 16:16:54
ganesh wrote:See Circle Equations in MathIsFun/MathsIsFun.
Many more topics are covered in the MathIsFun/MathsIsFun website.
The 'Help me' topic is given to those who are in need.
An example can be provided; the members are expected to do the practice problems by themselves.
I may leave this site soon. I find that there isn't much participation here. I cannot even upload pictures needed for certain math problems. I made a few friends but that's about it, honestly. I am currently seeking a new math site.
It's too bad that yahoo answers has shut down. We all know that this is due to the current administration in Washington, DC. The main goal is to control the masses and to keep people from communicating with each other. This is happening everywhere across the internet.
Yahoo Answers was(overwhelmingly so, barring a few people) a cesspool of idiots asking simplistic math questions, throwing around vitriolic and toxic messages about people(or groups), and bots.
Pretty sure Verizon(the parent corp of Yahoo!) decided to cut the cord so to speak, as it has no profitable incentive for keeping the site up.
That being said, I am sad to see such a titan of the old web fall.
#49 Re: Help Me ! » NFL Playing Field » 2021-04-27 00:44:10
Bob wrote:Yes, that perimeter formula is the place to start. Put in y and x and the known value for P. then it's just a case of making y the subject of the equation.
Then area = xy so you can use that equation for y to get area in terms of x only.
Bob
What about part B?
This is a classic optimization problem - just graph A(x) and find its local maximum in a "reasonable" domain of x(i.e, from 0 to 520/3, as area can't be negative.)
#50 Re: Help Me ! » Standard Form of the Equation » 2021-04-27 00:37:29
Bob wrote:If (a,b) is the centre of the circle and the radius is r then the equation will be
(x-a)^2 + (y-b)^2 = r^2.
This comes from Pythagoras' theorem.
For the first one you have both the centre and a point on the circumference so you can work out r.
For the second the centre will be half way along the diameter and the radius is half the length of the diameter,
Bob
For the second one, the midpoint formula comes into play, right?
Yes, it would.