Gist
The classic Trans-Siberian Railway runs from Moscow in European Russia to Vladivostok on the Pacific coast, crossing nearly 9,289 kilometers (5,772 miles) and eight time zones, making it the world's longest railway line, with branches extending to destinations like Beijing (Trans-Mongolian) and China (Trans-Manchurian).
The Trans-Siberian Railway, historically known as the Great Siberian Route and often shortened to Transsib, is a large railway system that connects European Russia to the Russian Far East. Spanning a length of over 9,289 kilometers (5,772 miles), it is the longest railway line in the world.
Summary
The Trans-Siberian Railway, historically known as the Great Siberian Route and often shortened to Transsib, is a large railway system that connects European Russia to the Russian Far East. Spanning a length of over 9,289 kilometers (5,772 miles), it is the longest railway line in the world. It runs from the city of Moscow in the west to the city of Vladivostok in the east.
During the period of the Russian Empire, government ministers—personally appointed by Alexander III and his son Nicholas II—supervised the building of the railway network between 1891 and 1916. Even before its completion, the line attracted travelers who documented their experiences. Since 1916, the Trans-Siberian Railway has directly connected Moscow with Vladivostok. As of 2021, expansion projects remain underway, with connections being built to Russia's neighbors Mongolia, China, and North Korea. Additionally, there have been proposals and talks to expand the network to Tokyo, Japan, with new bridges or tunnels that would connect the mainland railway via the Russian island of Sakhalin and the Japanese island of Hokkaido.
Route
The railway is often associated with the main transcontinental Russian line that connects many large and small cities of the European and Asian parts of Russia. At a Moscow–Vladivostok track length of 9,289 kilometers (5,772 miles), it spans a record eight time zones. Taking eight days to complete the journey, it was the third-longest single continuous service in the world, after the Moscow–Pyongyang service 10,267 kilometers (6,380 mi) and the former Kiev–Vladivostok service 11,085 kilometers (6,888 mi), both of which also follow the Trans-Siberian for much of their routes.
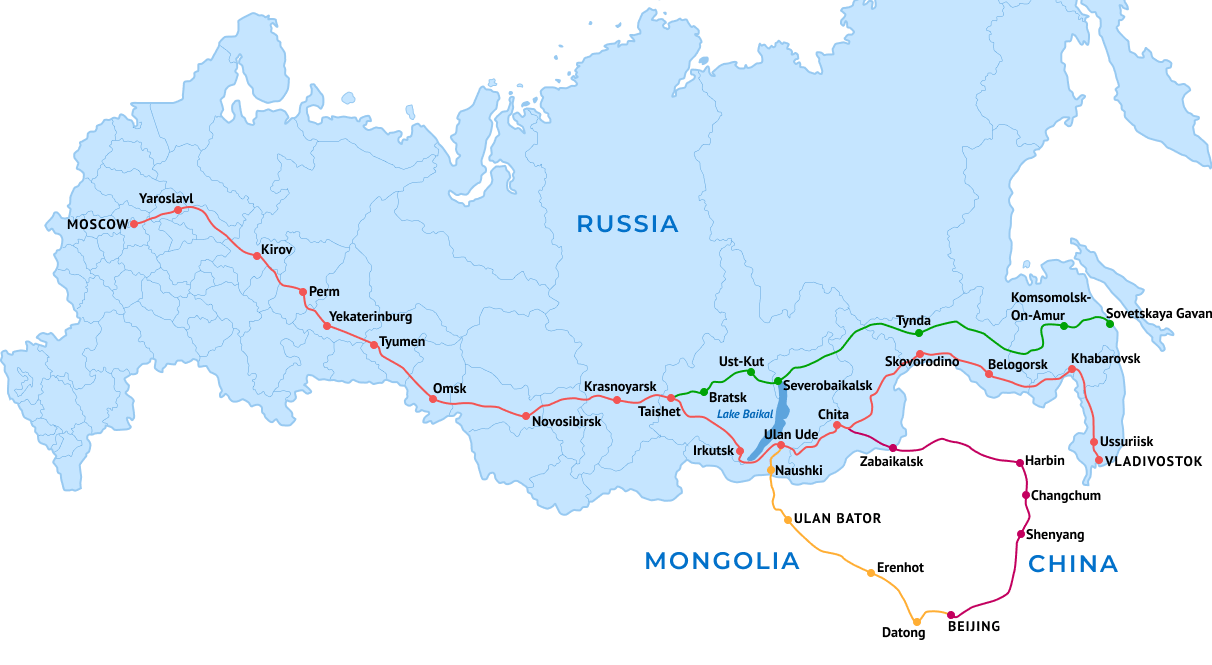
The main route begins in Moscow at Yaroslavsky Vokzal, runs through Yaroslavl or Chelyabinsk, Omsk, Novosibirsk, Krasnoyarsk, Irkutsk, Ulan-Ude, Chita, and Khabarovsk to Vladivostok via southern Siberia. A second primary route is the Trans-Manchurian, which coincides with the Trans-Siberian east of Chita as far as Tarskaya (a stop 12 km (7 mi) east of Karymskoye, in Chita Oblast), about 1,000 km (621 mi) east of Lake Baikal. From Tarskaya the Trans-Manchurian heads southeast, via Harbin Harbin–Manzhouli railway and Mudanjiang Harbin–Suifenhe railway in China's Northeastern provinces (from where a connection to Beijing is used by one of the Moscow–Beijing trains), joining the main route in Ussuriysk just north of Vladivostok.
The third primary route is the Trans-Mongolian Railway, which coincides with the Trans-Siberian as far as Ulan-Ude on Lake Baikal's eastern shore. From Ulan-Ude the Trans-Mongolian heads south to Ulaanbaatar before making its way southeast to Beijing. In 1991, a fourth route running further to the north was finally completed, after more than five decades of sporadic work. Known as the Baikal–Amur Mainline (BAM), this recent extension departs from the Trans-Siberian line at Taishet several hundred miles west of Lake Baikal and passes the lake at its northernmost extremity. It crosses the Amur River at Komsomolsk-na-Amure (north of Khabarovsk), and reaches the Tatar Strait at Sovetskaya Gavan.
Details
Trans-Siberian Railroad, the longest single rail system in the world, stretching 5,771 miles (9,288 km) across Russia between Moscow and Vladivostok. If its connection to the port station of Nakhodka is also included, the system reaches a total of 5,867 miles (9,441 km). The Trans-Siberian Railroad has had a profound effect on the region of Siberia as well as great importance in the economic and military history of the Russian Empire and the Soviet Union.
The main track length of the Trans-Siberian Railroad between Moscow and Vladivostok spans eight time zones and involves a journey time of seven days. Its western terminus is the Yaroslavsky station in Moscow, although a connecting service can be used to go farther west to St. Petersburg on the Baltic Sea. Moving eastward from Moscow, the railroad’s main route passes through Yekaterinburg and crosses the Ural Mountains before reaching Novosibirsk on the Ob River and then Krasnoyarsk on the Yenisey River. The route extends through Irkutsk and Ulan-Ude, following the southern shore of Lake Baikal between those cities, and then moves roughly in parallel to Russia’s border with Mongolia and then China before arriving at Khabarovsk on the Amur River and, finally, at Vladivostok on the Sea of Japan (East Sea).
A secondary route of the Trans-Siberian Railroad branches out at Ulan-Ude. For trains traveling eastward, it heads south to Mongolia’s capital, Ulaanbaatar, and onward to Beijing, China. This route is known as the Trans-Mongolian Railroad. A third route, the Trans-Manchurian Railroad, turns southeast after Lake Baikal and goes to the Chinese cities of Harbin and Mudanjiang before rejoining the main track just before Vladivostok. The Trans-Manchurian Railroad also provides service to P’yŏngyang, North Korea.
Throughout its history, Siberia has been subject to particularly harsh winter weather, and efforts to develop the region, beginning with Russian occupation of it during the 16th century, made little progress until well into the 19th century because of the absence of good roads. Horse-drawn sledges were the common mode of transport in winter, and in the summer months river navigation was used. Early attempts to set up a railway in the region were a response to the Russian Empire’s colonization of Siberia. Colonizing forces had to either transport essentials from Russian lands in the west or import them from China and Korea. However, progress on building a railway was slow because of the Russian bureaucracy and because Siberia was not, at the time, considered commercially important enough to invest in new infrastructure.
Russia’s focus during the later 19th century was on Central Asia, which was seen as a buffer zone between the Russian Empire and the British-ruled Indian subcontinent. Both powers engaged in the “Great Game” to consolidate their presence in Central Asia and to influence the many khanates of the region. The British advanced to Afghanistan, while the Russians eventually annexed the khanates of Khiva and Bukhara. Russia built the Trans-Caspian Railroad, which in 1888 reached Samarkand in present-day Uzbekistan, putting Afghanistan at risk of Russian invasion.
Russia’s focus shifted east under the vision of Sergei Witte, who, while working within the Russian ministry of finance, convinced Alexander III in 1891 to begin construction of what would become the Trans-Siberian Railroad. The intent was to extend Russian influence into East Asia and to capture global trade from British hands. The railway would allow merchandise and raw materials to be transported from Europe to the Pacific in half the time it took by sea. It would thus be attractive to traffic by other countries as well, threatening British domination on their traditional sea routes. So, too, the railway would allow the extraction of hitherto untapped resources in Siberia.
Work on the Trans-Siberian Railroad proceeded simultaneously in several sections. It was built concurrently in three stretches. The first stretch was the West Siberian Railroad from Chelyabinsk to the Ob River, completed in 1896. The second stretch, the Central Siberian Railroad, was from the Ob River to Irkutsk on the western shore of Lake Baikal; it was completed in 1899. The third stretch was the East Siberian Railroad from Ulan-Ude on the eastern shore of Lake Baikal to Vladivostok.
By early 1901 only about 1,240 miles (2,000 km) of the line remained to be built before a direct connection between Europe and the Pacific Ocean could be completed. But, due to Siberia’s harsh climate and geological conditions, the line was continued via a southerly section through Manchuria in China. In 1903 this Russian-built Chinese Eastern Railway was put into operation. Lake Baikal, however, was still a barrier: cargo and passengers had to cross the lake by ferry until a rail line around Lake Baikal was put into operation in 1905.
But the segment of the Trans-Siberian Railroad in Manchuria was to have consequences for Russia. In 1900 the Boxer Rebellion took place in China, targeting “foreign devils” and seeking to drive them out. Rebels in Manchuria had a specific grievance against the railroad, which they believed was responsible for upsetting the harmony of the region and causing droughts and flooding. The Russians moved 170,000 troops into Manchuria to protect their investment there, raising alarm in Japan over Russian intentions. Tensions were not eased by a new group of ministers in Moscow who had edged Witte out; they favoured a more aggressive foreign policy and refused to withdraw troops from Manchuria.
The Japanese attacked the Russian naval base at Port Arthur on the night of February 8–9, 1904, which was the start of the Russo-Japanese War. The war showcased the limitations of the railway, with its single-line route causing bottlenecks in the movement of troops and supplies. If one train with wounded troops was moving west, for instance, another train headed east with critical supplies had to wait at a station until the first had passed. After heavy losses in the 18-month war, Russia built a longer route, the Amur Railroad, to Vladivostok through its own territory so as to guard against the risk of Manchuria being taken over by the Japanese. In 1916 there was finally a Trans-Siberian Railroad wholly within Russian territory. Its completion marked a turning point in the history of Siberia, opening up vast areas to exploitation, settlement, and industrialization.
During the Russian Civil War that took place after the revolution in 1917, the Trans-Siberian Railroad was used by anticommunist forces to move troops, including Canadian reinforcements, westward from Vladivostok. Communist forces had to resort to blowing up bridges and sections of track to defeat them.
During World War II the nonaggression pact between the Germans and the Soviets enabled Nazi Germany to use the Trans-Siberian Railroad for the movement of goods to and from Japan. The railway also provided thousands of Jews a means of escaping Europe, using an eastward route to Vladivostok before sailing to the United States. After Germany invaded the Soviet Union and drove the Soviet Union to join the Allies, the railway allowed the U.S. to move much-needed supplies to the European front via the Pacific. The trans-Manchurian line came under full Chinese control only after World War II; it was renamed the Chinese Changchun Railway. During the Soviet era, a number of spur lines were built that radiated from the main trans-Siberian line. From 1974 to 1989 construction was completed on a large alternative route, the Baikal-Amur line; its route across the challenging environment of taiga, permafrost, and swamps made upkeep difficult. The Trans-Siberian Railroad was underused in the aftermath of the collapse of the Soviet Union but then saw a resurgence, due to improving economic conditions in Russia and tourism, at the turn of the millennium. Thawing permafrost due to climate change is, however, putting parts of the line at risk and leading to an increase in maintenance costs.
More than 85,000 people are estimated to have been involved in the construction of the Trans-Siberian Railroad. It remains the backbone of the Russian railway network, and today it is a double-track electrified line that has enabled millions of people to travel across Russia.
Additional Information
As soon as it was built at the beginning of the 19th century, the Trans-Siberian Railway was proclaimed the finest of the diamonds on the crown of the Russian Empire and became famous to the whole world. Since then, it is attracting many travelers striving to see the miracle of engineering and to experience the peculiar way of journey. At the same time, the Trans-Siberian regular trains are mostly used by locals for their commuting needs, so it is an excellent way to meet the real people and feel the pure soul of the country. The Trans-Siberian Railway uniquely combines romantic ideas about traveling with absolutely incomparable landscapes and unique impressions; all this makes the trip once-in-a-lifetime adventure.
Trans-Siberian routes
The original Trans-Siberian Railway connects Moscow and Vladivostok, covers 9829 km and crosses eight time zones, being the longest railway in the world. It will take seven days to travel from Moscow to Vladivostok without stops. In Ulan-Ude, the mainline branches in three directions. The Trans-Siberian section extends to Vladivostok, the Trans-Manchurian line goes through Northern China to Beijing, and the Trans-Mongolian line also ends in the capital of China but passes through Ulan Bator. Take a look at the Trans-Siberian route map and imagine all the possibilities the Trans-Siberian Railway can offer to tourists.
Transsiberian nonstop by direct regular trains
If the purpose of the journey is to cross the maximum distance by rail in the shortest time, if enjoying the scenery from the window and communicating with fellow will give you enough impressions, then all you need is to buy a ticket for a direct train along the Trans-Siberian, Trans-Mongolian or Trans-Manchurian route nonstop. The original Tran-Siberian trip will take 7 days, the Trans-Manchurian trip - 6 days, and a train ride to Ulan-Bator - about 5 days. You can visit the pages of these routes on our website and see the train schedule from Moscow to Vladivostok, Beijing, or Ulan Bator.






:max_bytes(150000):strip_icc():format(webp)/79588918-56a1323e5f9b58b7d0bcf3a1.jpg)


