Math Is Fun Forum
Discussion about math, puzzles, games and fun. Useful symbols: ÷ × ½ √ ∞ ≠ ≤ ≥ ≈ ⇒ ± ∈ Δ θ ∴ ∑ ∫ π -¹ ² ³ °
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2008-07-13 01:11:28
- Identity
- Member

- Registered: 2007-04-18
- Posts: 934
Families of functions
Consider the function with the rule
. Find the equation of the tangent of the curve y = f(x) at the point where .aaaah I can't get my head around this! The solution skips a lot of steps, so I find it hard to follow, can someone help me please?
Offline
#2 2008-07-13 02:27:09
- JaneFairfax
- Member

- Registered: 2007-02-23
- Posts: 6,868
Re: Families of functions
Note that if
then while if then .Hence
for .Last edited by JaneFairfax (2008-07-13 02:30:43)
Offline
#3 2008-07-13 03:05:35
- JaneFairfax
- Member

- Registered: 2007-02-23
- Posts: 6,868
Re: Families of functions
Right, heres a geometric interpretation.
The curve
has the following shape: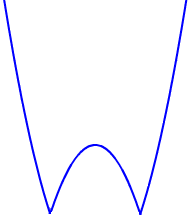
Its a curve with two downward-pointing prongs, the tips of the prongs being
and . When a > 0, the prong is to the right of the origin; When a < 0, its to the left of the origin. In either case, the maximum point is at , and the point at is always between the origin and the maximum point.Offline
#4 2008-07-13 04:54:06
- Identity
- Member

- Registered: 2007-04-18
- Posts: 934
Re: Families of functions
Oh ok, I think I get it, thanks JaneFairfax!
Is the answer
?Last edited by Identity (2008-07-13 04:54:55)
Offline
#5 2008-07-13 05:18:58
- JaneFairfax
- Member

- Registered: 2007-02-23
- Posts: 6,868
Re: Families of functions
Looks good to me. ![]()
Offline
Pages: 1