Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#151 2013-10-21 02:00:44
- Stangerzv
- Member
- Registered: 2012-01-30
- Posts: 266
Re: My New Twin Prime Numbers
Hi Bobbym
It would take some times and I would let you know when it is done.
Offline
#152 2013-10-21 02:20:48
- phrontister
- Real Member

- From: The Land of Tomorrow
- Registered: 2009-07-12
- Posts: 4,823
Re: My New Twin Prime Numbers
Hi Bobby,
Oh boy, if only some of that were true. My cousin is being kind.
I'm sure I asked you a question once...I think...possibly...
I can't find it, though. Tried inputting a question mark in Search for posts of mine that had one of those things, but that didn't do it. Hmmm...maybe I was wrong.
"The good news about computers is that they do what you tell them to do. The bad news is that they do what you tell them to do." - Ted Nelson
Offline
#153 2013-10-21 02:29:46
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: My New Twin Prime Numbers
About the question mark or the question?
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#154 2013-10-21 02:37:17
- phrontister
- Real Member

- From: The Land of Tomorrow
- Registered: 2009-07-12
- Posts: 4,823
Re: My New Twin Prime Numbers
About ever asking you a question (just going along with the doubt you expressed).
I thought that doing a search for my posts containing a question mark would bring up all posts where I had asked a question, and I was planning to then look through them to see if I'd ever asked you one.
"The good news about computers is that they do what you tell them to do. The bad news is that they do what you tell them to do." - Ted Nelson
Offline
#155 2013-10-21 02:40:53
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: My New Twin Prime Numbers
Try *?*
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#156 2013-10-21 02:47:30
- phrontister
- Real Member

- From: The Land of Tomorrow
- Registered: 2009-07-12
- Posts: 4,823
Re: My New Twin Prime Numbers
I already did, and it only returned 129 pages of my posts in descending date order. The first few I checked didn't have a question mark.
Maybe I've never asked a question.
"The good news about computers is that they do what you tell them to do. The bad news is that they do what you tell them to do." - Ted Nelson
Offline
#157 2013-10-21 02:50:11
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: My New Twin Prime Numbers
For some reason "?" is considered something else in the search.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#158 2013-10-21 02:58:32
- phrontister
- Real Member

- From: The Land of Tomorrow
- Registered: 2009-07-12
- Posts: 4,823
Re: My New Twin Prime Numbers
I'm pretty sure the search is limited, as we discussed recently in another thread. Only whole words work, I think, and some words are excluded.
I need to get some beauty sleepzzz......
Last edited by phrontister (2013-10-21 03:03:42)
"The good news about computers is that they do what you tell them to do. The bad news is that they do what you tell them to do." - Ted Nelson
Offline
#159 2013-10-21 03:45:09
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: My New Twin Prime Numbers
Hi;
Okay, see you later. It looks like I will be doing the same thing.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#160 2014-10-18 00:54:53
- Stangerzv
- Member
- Registered: 2012-01-30
- Posts: 266
Re: My New Twin Prime Numbers
Anybody knows how to run the primality test using AKS? Here the AKS article http://en.wikipedia.org/wiki/AKS_primality_test#History_and_running_time (I need for dummies instruction). I have ran ProvablePrimeQ[n] on the mathematica and even after more than a month still couldn't get the answer and it crashed my computer after sometimes. I need to make sure the primes here are true (especially for the large numbers).
Offline
#161 2014-10-18 11:00:45
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: My New Twin Prime Numbers
It has been pointed out to me that it is very, very, slow.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#162 2014-10-18 22:57:44
- Stangerzv
- Member
- Registered: 2012-01-30
- Posts: 266
Re: My New Twin Prime Numbers
Dear bobbym
Thanks for the info. I think I need to upgrade my computing power to do the job.
Offline
#163 2014-10-18 23:01:00
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: My New Twin Prime Numbers
I do not think so. It is very, very, very slow. Too slow to be useful except for small numbers.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#164 2014-10-20 03:28:08
- danaj
- Member
- Registered: 2014-03-03
- Posts: 29
Re: My New Twin Prime Numbers
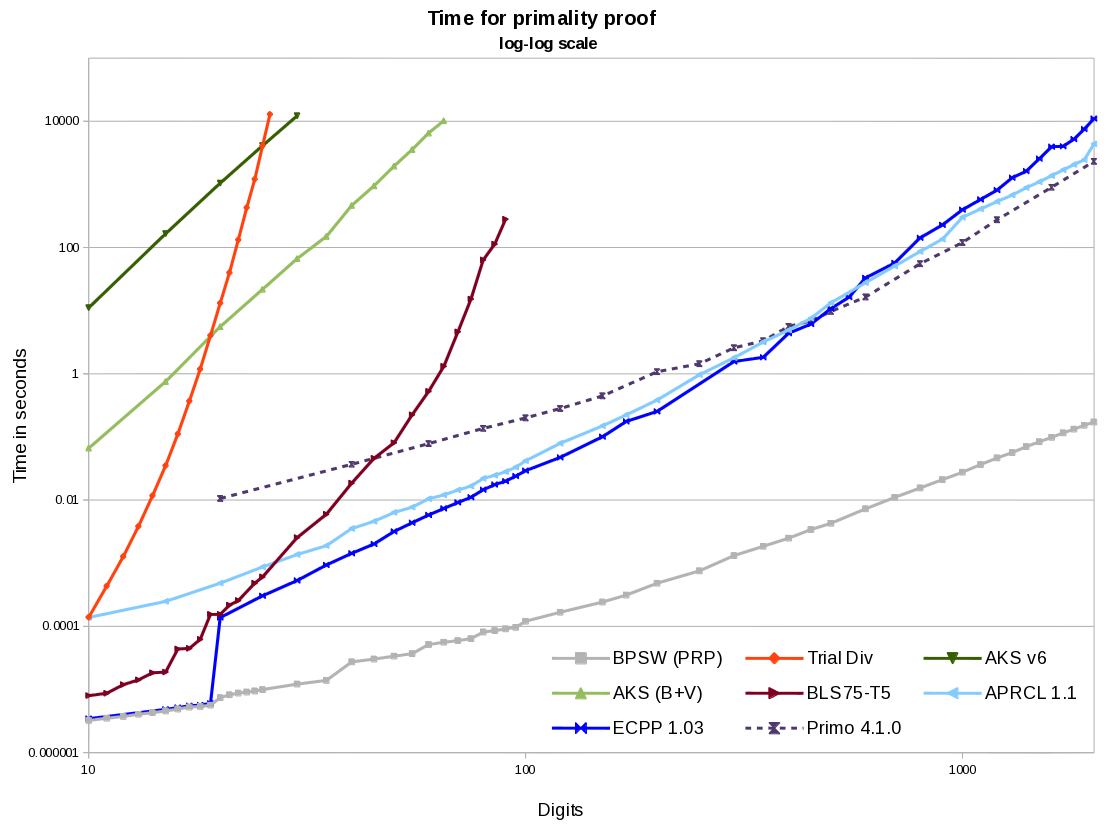
Here is an example graph showing some times for primality proving. Single threaded on a 4.3GHz machine (more details available if you'd like). I have not seen a faster AKS implementation than the B+V version here, but they could be out there. Pari/GP's APR-CL (the isprime command) runs a bit slower than WraithX's APRCL 1.1. I have no idea how fast Mathematica is (timings from this thread make me think its BPSW is quite a bit slower than the graph here, but that is independent from its proof times). Primo is the most common program used for proving large general primes.
100 digit primes can be proved extremely fast (a few milliseconds). 1000 digits will take ~2-8 minutes. For ECPP and APR-CL the time increases at about the 4th power of the number of digits (for AKS it's the 6th power). By 20k digits, expect 3 months using all cores of a 4- or 6-core machine.
I'm not sure about the various DR-restricted numbers, but the first set of unrestricted (post 109) are fairly small. E.g. p=29 => n=932651 is 213 digits, p=31 => n=2547137 is 242 digits. They grow of course, as p=59 => n=4183583 is 469 digits.
Offline
#165 2014-10-20 12:06:54
- Stangerzv
- Member
- Registered: 2012-01-30
- Posts: 266
Re: My New Twin Prime Numbers
Thanks danaj
I think having a computer with GPU processing units (NVIDIA Tesla) would make it faster due to the fact it has thousand cores per GPU. I am still working on building one with multiple GPUs, got to wait until the GPU price going down after sometimes.
Last edited by Stangerzv (2014-10-20 12:07:18)
Offline
#166 2014-10-20 17:10:23
- danaj
- Member
- Registered: 2014-03-03
- Posts: 29
Re: My New Twin Prime Numbers
Having 1024 nodes with 4 2880-core GPUs each doesn't solve anything if there isn't an application to run on it. Do you have something in mind?
Trial division would be trivial to parallelize, but is basically worthless. I see a paper by Asaduzzaman et al. from 2014 saying they have sped it up on GPUs, but (1) that's not hard, and (2) their comparison CPU code is 100x slower than the single-core CPU code I use, making their 90x speedup claim dubious. One thing that bothered me at GTC was the uncertainty around speedup numbers -- it's easy to get 100x speedup if you write cruddy CPU code in a weekend and then compare to GPU code you had four people working 6 months on.
AKS should be pretty easy to run in parallel (each of the s tests are independent), and the code that takes 99% of the time is pretty simple. You need to do lots and lots and lots of s += (a * b) % n type operations. Some problems:
[list=*]
[*]The growth rate difference means ECPP or APRCL on a single host will beat the hundreds of thousands of GPU cores running AKS. If the serial algorithm takes many trillions of years, how many cores will we need to make it run in an hour? Do you have that many GPUs?[/*]
[*]There is no certificate, so realistically your saying you ran this is no better than just saying you used well-known software to run BPSW + a Frobenius test + some number of random-base M-R tests. Less for me because I've seen too many broken AKS implementations. It doesn't matter how fast it is if it isn't correct.[/*]
[/list]
There may be other tricks for AKS that can help, but you have to make major changes to it to get it to the same growth rate as APR-CL or ECPP. There are definitely some research opportunities here.
The BLS75 methods involve factoring, so won't scale to usefully large numbers.
I don't know how well APRCL would parallelize. I think there was a thesis about the subject, but it didn't give much detail.
ECPP certainly could benefit if you could write it. If you do, please make it open source and publicize it. That would be a major accomplishment of use to many people. There are quite a few places where things could run in parallel (the fanout is extremely large if you run speculatively).
Last edited by danaj (2014-10-20 17:13:18)
Offline
#167 2014-10-23 08:45:37
- hemiboso
- Member
- Registered: 2014-10-23
- Posts: 4
Re: My New Twin Prime Numbers
Employing a modulo 30 factorization wheel as an analytical tool, coupled with deductive logic, I believe one can prove that all twin primes other than (3,5) or (5,7) must have digital root sequencing of either {2,4}, {8,1} or {5,7}, i.e., there can be no twin primes that sequence with digital roots {7,1}. Though not stated explicitly, I believe one can find all the elements needed to construct a proof at primesdemytified.com/twinprimes. Regardless, here is an outline of the steps I would propose:
1. Narrow the field to natural numbers ≡ to {1,7,11,13,17,19,23,29} modulo 30 (oeis.org/A007775). This infinite sequence is commonly known as “numbers not divisible by 2, 3 or 5,” and by definition contains all prime numbers > 5 and their multiplicative multiples. Thus we exclude prime numbers 2, 3 and 5 from our analysis, and the two pairs of twin primes that 3 and 5 are members of: (3,5) and (5,7).
2. Populate a modulo 30 factorization wheel with the above-defined sequence where 1 = 12°. Upon doing so, numbers ≡ to {1,7,11,13,17,19,23,29} modulo 30 are evenly distributed along 8—and only 8—radii: {12°, 84°, 132°, 156°, 204°, 228°, 276°, 348°} and have a repetition cycle of 1{+6+4+2+4+2+4+6+2} {repeat…}. Each rotation around the wheel increments a difference sequence of +30 (for example, numbers ≡ {1} modulo 30 increment as follows: 1, 31, 61, 91, 121, 151, 181 … ). And therefore, in digital root terms, every rotation around the wheel increments each of the 8 radii by +3.
3. Upon completing Step 2, we see that the twin prime candidate field can be further reduced given that numbers radiating at 84° (or numbers ≡ {7} modulo 30) and 276° (or numbers ≡ {23} modulo 30) cannot possibly be twin primes given the closest prime numbers in proximity to numbers ≡ {7} modulo 30 is +4 and for numbers ≡ {23} modulo 30 is -4. We have now winnowed the field of twin prime candidates to numbers ≡ {1,11,13,17,19,29} modulo 30 (oeis.org/A230462) which has a repetition cycle of 11{+2+4+2+10+2+10+2} {repeat…}. The sequence that remains, when consolidated into a single number line, accounts for exactly 20% of natural numbers and consists exclusively of twin prime candidates (n, n+2), starting with (11,13).
4. We now note, given that each rotation around our sieve increments 8 elements +30 {repeat …}, the digital root sequencing of each radius increments by digital root +3. Thus, the digital root sequencing of the 8 radii have a deterministic dependence upon the initial digital root state of the first 8 elements of the sequence where 1, 7, 11, 13, 17, 19, 23, 29 translates to digital roots 1, 7, 2, 4, 8, 1, 5, 2. The 8 radii thus sequence as:
numbers ≡ {1} modulo 30 sequence as {1,4,7} (or 1+3=4; 4+3=7; 7+3=1; repeat ... you get the drill ...)
numbers ≡ {7} modulo 30 sequence as {7,1,4}
numbers ≡ {11} modulo 30 sequence as {2,5,8}
numbers ≡ {13} modulo 30 sequence as {4,7,1}
numbers ≡ {17} modulo 30 sequence as {8,2,5}
numbers ≡ {19} modulo 30 sequence as {1,4,7}
numbers ≡ {23} modulo 30 sequence as {5,8,2}
numbers ≡ {29} modulo 30 sequence as {2,5,8}
5. As stated in Step 3, for the purposes of examining twin prime digital root sequencing, we can ignore numbers ≡ {7, 23} modulo 30, leaving us with numbers ≡ {1,11,13,17,19,29} modulo 30, and their corresponding deterministic digital root sequencing:
numbers ≡ {1} modulo 30 sequence as {1,4,7}
numbers ≡ {11} modulo 30 sequence as {2,5,8}
numbers ≡ {13} modulo 30 sequence as {4,7,1}
numbers ≡ {17} modulo 30 sequence as {8,2,5}
numbers ≡ {19} modulo 30 sequence as {1,4,7}
numbers ≡ {29} modulo 30 sequence as {2,5,8}
When we pair these as n, n+2 dyads (twin prime candidate couplings) we see that:
Numbers ≡ {11,13} mod 30 sequence as:
(11,13) = digital roots {2,4}
(41,43) = digital roots {5,7}
(71,73) = digital roots {8,1}
{digital roots repeat …}
Numbers ≡ {17,19} mod 30 sequence as:
(17,19) = digital roots {8,1}
(47,49) = digital roots {2,4}
(77,79) = digital roots {5,7}
{digital roots repeat …}
Numbers ≡ {29, 1} mod 30 sequence as:
(29,31) = digital roots {2,4}
(59,61) = digital roots {5,7}
(89,91) = digital roots {8,1}
{digital roots repeat …}
And thus we conclude that all twin prime candidates of the form n, n+2 greater than (5,7) that are potentially p, p+2 distribute to one of three digital root dyadic sequences: {2,4} (oeis.org/A232880), {8,1} (oeis.org/A232882) or {5,7} (oeis.org/A232881) (and you’ll note that these decompose to {6,9,3}, the vertices of one of three rotating equilateral triangles, along with {1,4,7} and {2,5,8}, that interact to form tensor matrices representing the coordinates of {9/3} star polygons … but that’s another story …
Offline
#168 2014-10-23 22:59:45
- Stangerzv
- Member
- Registered: 2012-01-30
- Posts: 266
Re: My New Twin Prime Numbers
Dear danaj
Thanks for the insight, if I got plenty of free time surely I would do it.
To hemiboso, thanks for the input. It seems interesting.
Offline
#169 2014-10-24 10:35:30
- phrontister
- Real Member

- From: The Land of Tomorrow
- Registered: 2009-07-12
- Posts: 4,823
Re: My New Twin Prime Numbers
Hi,
primesdemytified.com/twinprimes
The correct spelling for that link is http://primesdemystified.com/twinprimes
"The good news about computers is that they do what you tell them to do. The bad news is that they do what you tell them to do." - Ted Nelson
Offline
#170 2014-10-24 18:07:03
- hemiboso
- Member
- Registered: 2014-10-23
- Posts: 4
Re: My New Twin Prime Numbers
Sorry 'bout that. Thanks for catching, Land of Tomorrow! btw, I've subsequently published my 'outline for a proof' at http://www.primesdemystified.com/twinprimesdigitalrootproof ... I copied the link, so the spelling s/b correct :-) Thanks again.
Offline
#171 2014-10-26 12:15:24
- Stangerzv
- Member
- Registered: 2012-01-30
- Posts: 266
Re: My New Twin Prime Numbers
Dear hemiboso
The twin primes we are talking about here are not the regular twin primes (i.e. with a gap of 2) but the prime numbers with a gap of +-n(number of primes used in the calculation as gap). Anyway, thanks for the insight.
Offline
#172 2014-10-27 06:22:37
- hemiboso
- Member
- Registered: 2014-10-23
- Posts: 4
Re: My New Twin Prime Numbers
Yeah, somehow my comment got posted to the wrong string. I thought I was somewhere else in this labyrinth :-).
Offline
#173 2014-10-31 05:00:04
- Stangerzv
- Member
- Registered: 2012-01-30
- Posts: 266
Re: My New Twin Prime Numbers
Just wondering, could Ps be prime for composite Pt?
Offline
#174 2014-10-31 05:07:55
- Stangerzv
- Member
- Registered: 2012-01-30
- Posts: 266
Re: My New Twin Prime Numbers
Ok Got one solution for Pt=4
Offline
#175 2015-06-22 04:16:14
- Stangerzv
- Member
- Registered: 2012-01-30
- Posts: 266
Re: My New Twin Prime Numbers
Twin Prime of Alternate Components, consider this equation:
Where
Last edited by Stangerzv (2015-07-13 06:31:40)
Offline