Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2017-06-21 01:13:44
- denis_gylaev
- Member

- Registered: 2015-03-19
- Posts: 66
Functions Problems
Hello, I do not know the answers to these problems.
1) 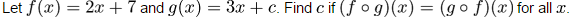
2) 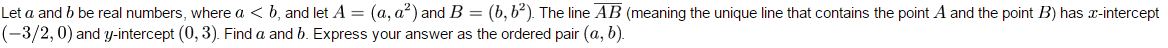
3) 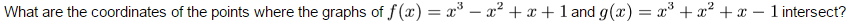
Offline
#2 2017-06-21 05:35:30
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,765
Re: Functions Problems
hi denis_gylaev
Q1) f o g means apply g and then f to the result:
f o g (x) = 2.(3x + c) + 7
Do a similar thing for g o f and set them equal.
Q2) This will get the equation of the line AB:
By substituting the known values of x and y you can get equations to find a and b.
Q3) Just set f and g equal and solve for x.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#3 2017-06-21 06:26:18
- denis_gylaev
- Member

- Registered: 2015-03-19
- Posts: 66
Re: Functions Problems
Hi Bob, thank you so much for the help.
For Q2, I got (-1,-2) and (1,2) and for Q3 I got (-1, 3)
However, I still do not understand what you mean for number 1. Please advise.
Offline
#4 2017-06-21 06:56:02
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,765
Re: Functions Problems
hi denis_gylaev
Think of a function as being a box into which you can input a number and another number is output. f and g are two such functions.
If you join the output from g to the input for f we get a composite function. To find out what single function is the same as the composite function you have to apply first g (which means you have an expression in x and put that through the second box for f.
g(x) = 3x + c so the box takes a number, times it by 3 and then adds c. If that is the input for the f box the output from f looks like this:
2(3x + c) + 7 The input is (3x + c) and this is times by 2 and 7 added.
So the composite function for (f o g) is 2(3x + c) + 7. You can simplify this yourself.
You might think at first that g o f will give the same result but it doesn't. First do f ... 2x + 7 and then make this the input into g ... 3(2x + 7) + c
We want these to be equal so just make an equation by putting them equal to each other. The x terms cancel out (why?) so you're left with an equation for c.
There is a MIF page on this here: http://www.mathsisfun.com/sets/function … ition.html
Note The x comes after the function letter [eg. f(x) not (x) f ] so when you want to apply a second function you have to put it before the first. eg g(f(x)) means apply f then g to the result. This can be confusing but think about log(sin(x)) for example. o is used to indicate that we are combining functions.
Hope that helps,
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
Pages: 1