Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#26 Re: This is Cool » My New Twin Prime Numbers » 2017-02-28 03:42:02
Smallest solution for Pt=7
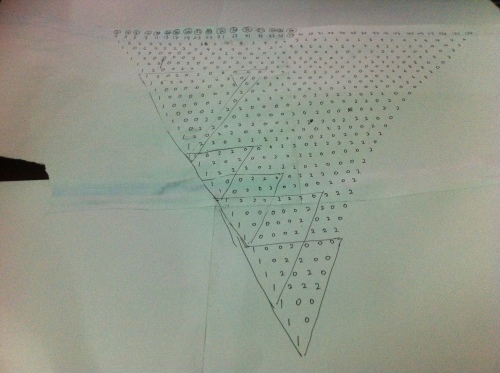
#27 This is Cool » Prime Numbers Disintegration Pattern » 2017-02-17 05:01:46
- Stangerzv
- Replies: 1
My latest research on the prime numbers pattern
#28 Re: This is Cool » My New Twin Prime Numbers » 2017-02-13 02:55:54
Smallest solution for Pt=6
#29 Re: This is Cool » My New Twin Prime Numbers » 2017-02-08 06:45:45
Smallest solution for Pt=5
#30 Re: This is Cool » My New Twin Prime Numbers » 2017-02-08 06:33:20
Another result for Pt=4
#31 Re: This is Cool » My New Twin Prime Numbers » 2017-02-08 06:00:44
Another result for Pt=3
#32 Re: This is Cool » My New Twin Prime Numbers » 2017-02-08 05:43:14
Another result for Pt=2
#33 Re: This is Cool » My New Twin Prime Numbers » 2017-02-01 03:45:19
I agree but in this case it seems that the primes love to hang out with primes more than the odd numbers.
#34 Re: This is Cool » My New Twin Prime Numbers » 2017-01-21 06:20:37
After lengthy calculation for bigger Pt, it seems the primes are harder to find. It is easier to find the primes when the series consisting of prime numbers instead of odd numbers.
#35 Re: This is Cool » My New Twin Prime Numbers » 2017-01-14 03:28:07
There is no apparent twin prime up to Pt=9 so far. The occurrence of the twin primes becoming scarce when the series are becoming larger.
#36 Re: This is Cool » My New Twin Prime Numbers » 2017-01-04 04:14:09
Let P1=2 and Pt=4
#37 Re: This is Cool » My New Twin Prime Numbers » 2016-12-26 11:27:50
Let P1=2 and Pt=3
#38 Re: This is Cool » My New Twin Prime Numbers » 2016-12-24 03:46:23
Consecutive Prime
#39 Re: This is Cool » Could be new prime Numbers using repdigits » 2016-11-22 18:48:55
Dear googol
p should be a prime whereas p=35=5x7, p=51=3x17, p=341=11x31
#40 Re: This is Cool » My New Twin Prime Numbers » 2016-07-06 00:15:34
There are lesser resultant primes using odd number inputs. The next prime for Pt=2 is given as follows
#41 Re: This is Cool » Fun with 0 / 0 » 2016-06-25 02:11:04
Basically 0/0 can be anything. Unless we tend to go beyond normal understanding of infinity, we can actually get 0/0=1. For example
let
Taking natural long on both sides yields
Then
If we could consider the "undefined" cancelling each other equal to zero.
Thus
We can argue like forever with this thing but this is how mathematics progresses ![]() Perhaps 0/0=An Apple:)
Perhaps 0/0=An Apple:)
#42 Re: This is Cool » Fun with 0 / 0 » 2016-06-21 19:51:54
If you have an equation of x=y, it is always passing through the coordinate {0,0}. Since,
it concludes that :)#43 Re: This is Cool » My New Twin Prime Numbers » 2016-06-17 17:58:13
Extension into odd numbers instead of using primes
Where
Example
#44 Re: This is Cool » My New Twin Prime Numbers » 2016-06-14 01:35:06
Extension into negative Primes
Example
#45 Re: This is Cool » My New Twin Prime Numbers » 2016-05-31 17:03:19
Dear Primenumbers, the idea of the equations is to get the largest primes or perhaps they simply non-existence as n goes into the infinity. There are several types of equations formed from the generalize equation (i.e. n=integers, n=primes, n=square numbers).
#46 Re: This is Cool » My New Twin Prime Numbers » 2016-04-30 22:20:46
The largest solution for
could be only when#47 Re: This is Cool » Grandi's series (1-1+1-1...) » 2016-01-16 12:06:06
You get funny values when you take all the infinities as the same. Infinity as a concept gives rise to many problems like S=1-1+1-...infinity=1/2 because we tend to take all the infinities as the same like (1+infinity)=infinity. What is the value of infinity/infinity? I am more to the concept that the Infinity has an origin and point of reference. For example, if we had a source of light that could travel forever into the infinity and is set to travel today and the another one would be set to travel tomorrow, are they the same value when they reach infinity?
If they do have the same value, I can show you that Riemman zeta function
not and many more.#49 Re: This is Cool » New Math Formula: Sums of Power for Arithmetic Series » 2015-11-19 10:43:50
The journal has been accepted for publication in the Journal of Discrete Mathematical Sciences & Cryptography
#50 Re: This is Cool » New Math Formula: Sums of Power for Arithmetic Series » 2015-09-26 12:08:23
This paper is about to be accepted. Then, I can update on the Wikipedia for a new formulation for sums of power of an arbitrary arithmetic progression.