Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#26 2005-07-19 16:51:33
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 52,569
Re: Problems and Solutions
Problem #6
A salesman's commission is 5% on all sales up to $10,000 and 4% on all sales exceeding this. He remits $31,100 to his parent company after deducting his commission. His sales was worth $_________.
It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#27 2005-07-19 19:06:43
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: Problems and Solutions
Why did the vector cross the road?
It wanted to be normal.
Offline
#28 2005-07-19 19:16:37
- MathsIsFun
- Administrator

- Registered: 2005-01-21
- Posts: 7,713
Re: Problems and Solutions
S = Sales
C = Commission
R = Remittance to Company after sales
For S <= $10,000, C = 0.05S
For S > $10,000, C = 500 + 0.04(S-10,000)
R = S - C
Now, we know that R = 31,100
So ... sorry, gotta go!
"The physicists defer only to mathematicians, and the mathematicians defer only to God ..." - Leon M. Lederman
Offline
#29 2005-07-19 19:25:30
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 52,569
Re: Problems and Solutions
31,100 = S - [500+0.04(s-10,000)]
31,100 = S -[500 + 0.04s - 400]
31,100 = S - 100 - 0.04s
31,200 = 0.96 S
S = 31,200 / 0.96
S = 32,500 ![]()
It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#30 2005-07-19 21:58:49
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 52,569
Re: Problems and Solutions
#7
The ratio of annual incomes of two persons is 9:7 and the ratio of their annual expenditure is 4:3. Each of them saves $2000 yearly. Find their annual incomes.
It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#31 2005-07-20 03:10:35
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: Problems and Solutions
Wow, four simultaneous equations...
Why did the vector cross the road?
It wanted to be normal.
Offline
#32 2005-07-20 09:41:07
- MathsIsFun
- Administrator

- Registered: 2005-01-21
- Posts: 7,713
Re: Problems and Solutions
BY THE WAY, since my little {hide}{/hide} tag is getting used a bit, it will soon become too late to rename it to {popup} or {boing} or whatever.
So, is "hide" the best name, then (even though it is just hidden under a little button)
"The physicists defer only to mathematicians, and the mathematicians defer only to God ..." - Leon M. Lederman
Offline
#33 2005-07-20 11:14:20
- im really bored
- Member
- Registered: 2005-05-12
- Posts: 76
Re: Problems and Solutions
For MathIsFuns lake problem I got 6,931,471.8055994530941723212145818 liters of water that needs to be added.
Offline
#34 2005-07-20 12:37:45
- Zach
- Member

- Registered: 2005-03-23
- Posts: 2,075
Re: Problems and Solutions
There's a Hide tag?!
Boy let me tell you what:
I bet you didn't know it, but I'm a fiddle player too.
And if you'd care to take a dare, I'll make a bet with you.
Offline
#35 2005-07-20 18:18:16
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: Problems and Solutions
For MathIsFuns lake problem I got 6,931,471.8055994530941723212145818 liters of water that needs to be added.
Was that with calculus or a more accurate version of my method?
Why did the vector cross the road?
It wanted to be normal.
Offline
#36 2005-07-20 19:21:56
- im really bored
- Member
- Registered: 2005-05-12
- Posts: 76
Re: Problems and Solutions
Nope no calculas or your method, I just got a tip from a friend that its related to the natural log of 2, which is 0.69314718055994530941723212145818.
Offline
#37 2005-07-20 19:27:16
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 52,569
Re: Problems and Solutions
Wow, four simultaneous equations...
There are only two:-
9x - 4y = 2,000
7x - 3y = 2,000
Solving for 'x', the annual income of the two can be calculated. They would be 9x and 7x. ![]()
Last edited by Jai Ganesh (2005-07-20 19:27:58)
It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#38 2005-07-21 16:35:07
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 52,569
Re: Problems and Solutions
Which is greater?
Cos (Sin A) or Sin (Cos A)?
It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#39 2005-07-21 17:57:18
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: Problems and Solutions
Degrees, radians or grads?
I can tell just by thinking about it the answer for degrees and grads, but if you're working with radians, there might be a few exceptions, though I doubt it.
Why did the vector cross the road?
It wanted to be normal.
Offline
#40 2005-07-21 18:14:40
- MathsIsFun
- Administrator

- Registered: 2005-01-21
- Posts: 7,713
Re: Problems and Solutions
Oooh ... (reaches for Excel) ...
cos(sin(a)) fluctuates between 0.734664609.. and 1
sin(cos(a)) fluctuates between 0.841470985.. and -0.841470985..
They cross over first at about 28.9° (0.5031796.. radians), then back again at 331.1° (5.779671333.. radians)
Now, are 0.734664609.., 0.841470985.. or 0.5031796.. magical numbers?
"The physicists defer only to mathematicians, and the mathematicians defer only to God ..." - Leon M. Lederman
Offline
#41 2005-07-21 18:51:40
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: Problems and Solutions
Plotting cos(sin a) against sin(cos a) in Excel gives a smiley mouth. The important thing, though, is to see whether one is always bigger than the other, and this graph cannot do that.
I plotted radian value against cos(sin a)-sin(cos a) and I got a beautiful swirly pattern. This pattern always stayed above 0, so cos(sin a) is always bigger than sin(cos a).
Why did the vector cross the road?
It wanted to be normal.
Offline
#42 2005-07-21 20:52:37
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 52,569
Re: Problems and Solutions
Cos(Sin A) is always greater than Sin (Cos A),
as rightly pointed out by Mathsy!
We shall test this for three values in the first quadrant, in degrees.
First, 0.01°.
Cos (Sin A) > Sin(CosA).
Next, for 45°
Again, Cos (Sin A) > Sin(CosA).
Finally, for 89.9°
Yet again, we get the same result.
I shall try to search for a proof, or prove it myself!
It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#43 2005-07-21 21:02:16
- MathsIsFun
- Administrator

- Registered: 2005-01-21
- Posts: 7,713
Re: Problems and Solutions
Ooops, my bad in some calculations.
Yes, I see same result now.
I will make up for my mistake by posting this nice graph that mathsy talked about:
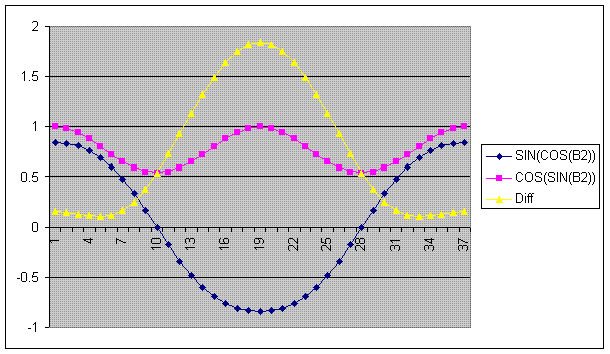
"The physicists defer only to mathematicians, and the mathematicians defer only to God ..." - Leon M. Lederman
Offline
#44 2005-07-21 22:07:33
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 52,569
Re: Problems and Solutions
Thank you, Admin, for the neat graph. ![]()
It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#45 2005-07-22 21:55:17
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 52,569
Re: Problems and Solutions
I just remembered a question asked to me when I participated in a quiz when I was 14 :
A three digit number is written on a window glass,
the difference between the number and as it can be seen from the other side is 693,
what's the number? ![]()
It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#46 2005-07-22 23:04:50
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: Problems and Solutions
Well, it has to be made up of 0's 1's and 8's (and maybe 2's and 5's that swap when reversed, depending on the writing style)
I've got , but there might be others.
Why did the vector cross the road?
It wanted to be normal.
Offline
#47 2005-07-29 19:54:39
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 52,569
Re: Problems and Solutions
Two candles A and B, of equal height but different circumferences, burn for 4 hours and 3 hours respectively. If the two are lit at the same time, after what time would one candle be half the height of the other? ![]()
It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#48 2005-07-29 22:02:39
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: Problems and Solutions
This is the closest answer I could find. I get about 3 minutes more than what the picture says.
Why did the vector cross the road?
It wanted to be normal.
Offline
#49 2005-07-31 18:54:04
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 52,569
Re: Problems and Solutions
As always, you are corect, Mathsy!
I shall show how I did it.
Assume both candles are 'h' inches in height.
The height of the first candle reduces by h/4 every hour and that of the second reduces by h/3.
Lets assume in time 't' hours, the first is twice the height of the second.
Therefore,
h - t(h/4) = 2 [h - t(h/3)]
h - ht/4 = 2h - 2ht/3
h = 2ht/3 - ht/4
h = 5ht/12
Cancelling h on both sides,
1 = 5t/12
or t = 12/5
The unit we had taken was hours,
therefore, in 12/5 hours, that is 2 2/5 hours, one will be double the height of the other.
Simplified, it is 2 hours and 24 minutes.
It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#50 2005-08-02 16:10:54
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 52,569
Re: Problems and Solutions
Problem #n
The distance between two cities is 840 kilometres.
If I start driving from one city to the other at a speed
5 kilometres/hour more than my normal speed,
I save 3 hours. What is my normal speed?
It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline