Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 Help Me ! » Initial Velocity Vector and Diagram from Parametric Equation » 2018-05-22 12:27:52
- Oran2009
- Replies: 1
I have a project where we have to throw an object and find the velocity of it. I have found the parametric equations of the path of the object to be:
I have found that the initial velocity vector is:
Firstly, is this correct?
Secondly, we are required to make a diagram showing the initial velocity vector and the components. How am I to do this accurately on the graph (in Desmos)?
#2 Re: Help Me ! » PreCalc Problems » 2017-08-28 02:12:39
I got it thanks!
#3 Re: Help Me ! » PreCalc Problems » 2017-08-27 11:19:43
wait... So I got something like this when I substituted and simplified?
v^2 = 124100 - 64h
#4 Re: Help Me ! » PreCalc Problems » 2017-08-27 08:11:44
Hi. I have solved the 2nd problem. But I still don't get the first question. How do I get the quadratic for h?
#5 Re: Help Me ! » Increasing, Decreasing, Even, Odd, and/or Invertible! » 2017-04-15 04:48:35
I know that increasing means that when x becomes larger, f(x) also becomes larger
Decreasing means that when x becomes larger, f(x) becomes smaller
Even is when f(x)=f(-x)
Odd is when f(x)=-f(-x)
But I don't know what invertible means... I think it means when you switch the x and y you still get the same equation???
#6 Help Me ! » Increasing, Decreasing, Even, Odd, and/or Invertible! » 2017-04-15 03:02:08
- Oran2009
- Replies: 3
For each of the following, determine if the function is increasing, decreasing, even, odd, and/or invertible on its natural domain:
e) f(x) = |x| * \sqrt{x}
Thanks!
#7 Help Me ! » Lucas Number Questions » 2017-04-02 01:50:13
- Oran2009
- Replies: 1
1) Find (a,b) such that
Where n is the nth lucas number.
How would I start this? Would I just start by plugging in a=b=1a=b=1 and then trying to solve?
#8 Help Me ! » Irrational Roots Questions » 2017-02-18 08:35:12
- Oran2009
- Replies: 2
1) Let f(x) = x^3+bx+c, where b and c are integers.
If f(5+\sqrt 3)=0, determine b+c.
I know that 5-\sqrt 3 is also a root, but how to continue?
----------------------------------------------------------------
2) Find a monic quartic polynomial f(x) with rational coefficients whose roots include . Give your answer in expanded form.
???
----------------------------------------------------------------
3) Suppose $P(x)$ is a polynomial of smallest possible degree such that:
-P(x) has rational coefficients
-P(-3) = P(\sqrt 7) = P(1-\sqrt 6) = 0
-P(-1) = 8
Determine the value of P(0).
???
#9 Help Me ! » Vectors Question - Direction and Speed » 2017-02-13 14:29:36
- Oran2009
- Replies: 1
Problem:
A skiff leaves a dock and heads toward a house across the river. The house is at a bearing of from the dock. There is a 1 mile per hour current blowing due east. Determine the speed and direction the skiff would have to maintain so that the skiff's actual speed is 4 miles per hour and moving directly towards the house.
I know you can solve this with vectors and using trigonometry, but how would I do this?
*You can use the law of sines to find the direction, but what about the speed? Is it just 4 miles?
#10 Help Me ! » Polynomial Proof » 2017-02-07 13:55:22
- Oran2009
- Replies: 1
Part 1:
Let f(x) and g(x) be polynomials.
Suppose f(x)=0 for exactly three values of x: namely, x=-3,4, and 8.
Suppose g(x)=0 for exactly five values of x: namely, x=-5,-3,2,4, and 8.
Is it necessarily true that g(x) is divisible by f(x)? If so, carefully explain why. If not, give an example where g(x) is not divisible by f(x).
Part 2:
Generalize: for arbitrary polynomials f(x) and g(x), what do we need to know about the zeroes (including complex zeroes) of f(x) and g(x) to infer that g(x) is divisible by f(x)?
(If your answer to Part 1 was "yes", then stating the generalization should be straightforward. If your answer to Part 1 was "no", then try to salvage the idea by imposing extra conditions as needed. Either way, prove your generalization.)
How to do this problem?
#11 Re: Help Me ! » Some Polynomial Problems » 2017-02-07 13:53:34
I got #1. The answer is just m=5
#12 Help Me ! » Some Polynomial Problems » 2017-02-07 13:02:38
- Oran2009
- Replies: 10
1) The polynomial
is divisible by $x-4$ and all of its zeroes are integers. Find all possible values of $m$.
Do I plug in x=4? What would I do???
-------------------------------------------------------------------------------------------------------------------------------------------
2) Suppose the polynomial is of degree and satisfies , , , and .
Determine the value of .
How to do this?
-------------------------------------------------------------------------------------------------------------------------------------------
#13 Help Me ! » Some Algebra Problems » 2017-02-05 15:49:55
- Oran2009
- Replies: 6
1) Find all integers for which is an integer.
For this problem, you can divide using synthetic division and get (n+2) with a remainder of 3. You can write
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
2) Suppose is a polynomial of degree or greater such that , , and .
Find the remainder when is divided by .
And I have no idea how to do this problem...
#14 Help Me ! » Circle Geometry Problems » 2016-07-09 07:56:53
- Oran2009
- Replies: 5
1) Let
, , and be points on a circle. Let and the tangent to the circle at intersect at . If , , and , then find .
2) In triangle , , , and . Let be the point on the circumcircle of triangle so that . Find .

Please help!
#15 Help Me ! » Circle Geometry Questions » 2016-06-30 07:31:09
- Oran2009
- Replies: 3
I have some problems that I would like full solutions and answers.. Please help me quick!
1) Let
be twelve equally spaced points on a circle with radius 1. Find(The sum includes the square of the distance between any pair of points, so the sum includes
2) Let
be a cyclic quadrilateral. Let be the intersection of and , and let be the intersection of and . Prove that the angle bisectors of and are perpendicular.
Please help me.
#16 Help Me ! » Circles Problem » 2016-06-18 07:27:01
- Oran2009
- Replies: 2
We are given a regular heptagon of side length 1. Let S be the set of points that are within a distance of 1 from some point on or inside the heptagon, but not including the heptagon itself. Find the area of S.
Please help!!!
#17 Help Me ! » Triangle Inequality Question » 2016-06-14 03:06:42
- Oran2009
- Replies: 1
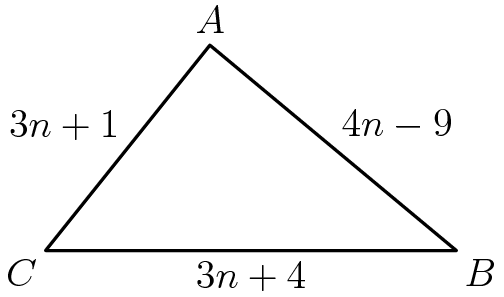
Two sides of an acute triangle are 8 and 15. How many possible lengths are there for the third side, if it is a positive integer?
I'm not sure if the word "acute" affects the problem...
If not, is the answer 15?
(Somehow LaTeX is not working...)
#18 Re: Help Me ! » Geometry Questions Please Help » 2016-06-13 14:58:46
Thanks! But what is your solution, I wonder?
#19 Re: Help Me ! » Geometry Questions Please Help » 2016-06-13 14:44:11
I think I fixed the link. Try again
Pages: 1