Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 Re: Help Me ! » Probability question on coin flipping » 2009-08-27 00:40:46
wow thanks!
#2 Re: Help Me ! » Probability question on coin flipping » 2009-05-27 13:53:38
wow that's some high level mathematics (for me). Never done this in high school. Thanks for taking the time to do this. If the coin was biased (e.g. 70% chance tails; 30% chance heads), how do i take that into account?
#3 Re: Help Me ! » Probability question on coin flipping » 2009-05-27 00:11:05
no one? ![]()
#4 Help Me ! » Probability question on coin flipping » 2009-05-26 14:06:28
- tongzilla
- Replies: 22
Hi guys, please help me with this problem (not homework, just wondering myself...)
What's the probability that I will flip 10 heads in a row exactly once if I flip a coin 1000 times. What about 10,000 times? Also, what's the probability that I will flip 10 heads in a row once or more if I flip the coin 10,000 times?
I know the probability that I will flip 10 heads in a row if I flip 10 times is 0.5^10=0.000977
But then I'm stuck after this...
Thanks!
#5 Re: Help Me ! » How to solve this problem? » 2007-10-20 20:57:44
But your chosen values of x[sub]A[/sub] and x[sub]B[/sub] will not satisfy the further conditions
Will they?
Just because
doesnt mean its up to you to choose any values greater than 1 for them if further conditions are being specified. You need to ensure that they satisfy those further conditions as well.
In this case, if you want P[sub]A[/sub] and P[sub]B[/sub] to be positive, certain values of x[sub]A[/sub] and x[sub]B[/sub] will not work.
Let me clarify what my actual question is. Sorry for not making this clear enough early on.
The question I am asking is this:
1) What restrictions (i.e. the general rule) are needed on
and so that there are some range of values of and to make both and positive?2) What is the restriction (i.e. the general rule) for
and such that no matter what combination of and is chosen (but still sums to 100), and is always negative?3) How can you prove your answers to questions 1) and 2) ?
#6 Re: Help Me ! » How to solve this problem? » 2007-10-20 09:09:54
Similarly
Jane, not sure if your solution works.
First, lets say
and
(I made these values up, but they satisfy my initial condition that they must be greater than one)
then this implies
and
So this doesn't satisfy my condition that
Second, given the these borderline values of
and (72.46 and 32.26), and are both negative (plug it into my initial equations to see yourself), and therefore can not be greater than zero. So the problem hasn't been solved.#7 Help Me ! » How to solve this problem? » 2007-10-20 03:06:01
- tongzilla
- Replies: 5
Problem:
1) Both
and is always greater than zero. Are there any restictions needed on for this to be true?===========================================
EDIT (21 OCT 07):
Let me clarify what my actual question is. Sorry for not making this clear enough early on.
The question I am asking is this:
1) What restrictions (i.e. the general rule) are needed on
and so that there are some range of values of and to make both and positive?2) What is the restriction (i.e. the general rule) for
and such that no matter what combination of and is chosen (but still sums to 100), and is always negative?3) How can you prove your answers to questions 1) and 2) ?
#8 Re: Puzzles and Games » Swimming with Sharks » 2006-11-11 20:49:02
O_O ...
Someone's created mathematical solutions to not getting eaten by sharks...
???
#9 Puzzles and Games » Swimming with Sharks » 2006-11-09 06:11:08
- tongzilla
- Replies: 3
Two friends, A and B, are at a beach for two days.
There is a probability p that the water has sharks. If any sharks are present, the swimmer will be attacked for sure.
A peaceful swim gives a payoff of 1.
Being attacked by a shark gives a payoff of of -c<0
Sitting on the beach gives payoff of 0.
If a swimmer is attacked by sharks on the first day, then any swimmer will definitely be attacked on the second day.
However, if at least one person swims on day one and is not attacked, then it is clear that there are no shaks, and no attacks will take place on day two.
If no one swims on day one, then nothing is learnt, and so the probability of shark infestation remains at p.
Each player seeks to maximise the sum of his expected payoffs over the two days.
Assume that 2(1-p)/p > c > (1-p)/p
Question:
In the above scenario, what is the best strategy? In other words, what should the peson do on day one? Please explain your answer.
Hint:
Consider first the case where only one person is present at the beach over two days. What is the best strategy for this person?
#10 Re: Puzzles and Games » Lions » 2006-11-09 05:59:28
Interesting puzzle.
Nice answer mathsyperson. If you can be bothered, try to polish your answer in the 3 lion case by using more logic in your backward induction. I.e. if Lion 3 blah blah blah then Lion 2 realises this so blah blah blah, etc.
So when does the game end?
#11 Puzzles and Games » Lions » 2006-11-09 03:17:00
- tongzilla
- Replies: 2
There are lions and a piece of prey.
If lion 1 doesn't eat the prey, the game ends.
If lion 1 does eat the prey, it gets slow and fat so lion 2 eats lion 1.
If lion 2 doesn't eat lion 1, the game ends.
If lion 2 does eat lion 1, then lion 2 may be eaten by lion 3.
Etc.
Each lion prefers to eat than be hungry. But it would rather be hungry than be eaten.
What is the logical (i.e. backward induction) outcome for any n number of lions?
#12 Re: Puzzles and Games » Coin Problem » 2006-08-22 15:29:52
Good thinking mathsyperson! You're the winner of a matching salt and pepper set! In fact, there are other "solutions" that seem to fit, but if you examine the amount of overlap you will realise that it doesn't correspond to the diagram shown in the question.
#13 Re: Puzzles and Games » Coin Problem » 2006-08-21 21:36:17
mathsyperson, good work!
So which is your FINAL answer out of the two?
I will post my solution soon.
In the mean time, can you tell me what the overlap is given your coin diameters? That should give you a clue ![]()
#14 Re: Puzzles and Games » Coin Problem » 2006-08-18 21:06:26
tt, no.
#15 Re: Puzzles and Games » Coin Problem » 2006-08-09 01:02:57
tt, no.
#16 Re: Puzzles and Games » Coin Problem » 2006-06-26 03:32:58
Still no one?
I can only see one way of doing this problem, so I would be interested in what other methods can be used to work this out.
I will submit my solution once there is more discussion!
#17 Re: Puzzles and Games » Coin Problem » 2006-06-20 07:04:37
No one wants to give this a go?
#18 Puzzles and Games » Coin Problem » 2006-06-19 20:07:07
- tongzilla
- Replies: 14
There are six identical coins with diameters a whole number of millimetres. I have started making a tray to stack them in, as shown:
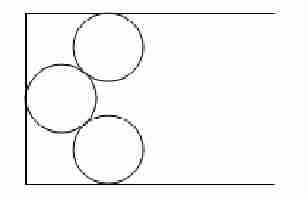
If I stacked the other three coins in the tray in a mirror image pattern of the first three, the smallest tray would be a two-figure number of millimetres wide. But if I repeated the above pattern, putting in a single coin next, then two on the right, the trays width could be reduced. In fact, it would be the same as before but with its two digits reversed.
What is the diameter of each coin?
Pages: 1