Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 Re: Help Me ! » Marquis De L'Hopital optimization problem » 2007-02-26 23:29:18
I get 0 = 2x^3 - 2.16x^2 +.16
Now you need the zeros of a cubic. Not sure how to get them.
From the graph of f'(x) we see that x=1 is a likely root. Use synthetic or polynomial division and verify that it is a root. Unfortunately f(1) doesn't make sense so we need to find other roots. From the division we have:
f'(x) = (x-1)(2x^2 - 0.16x - 0.16)
Then apply the quadratic, discard the nonsensical negative (discriminant) solution, leaving us
x = (0.16+sqrt(.0256+1.28))/4 ~= 0.326
and f(0.326) = .519 or 51.9 cm, which is indeed our solution.
Good work with the chain rule!
Best,
Kevin
#2 Re: Help Me ! » Marquis De L'Hopital optimization problem » 2007-02-23 21:09:16
I was going along those lines but I avoided the trig functions and stuck with Pythagoras.
I put it on a coordinate plane with the origin at the top left triangle vertex like so: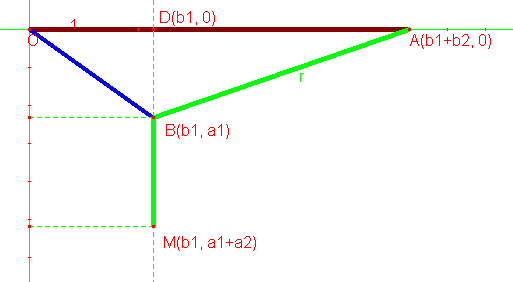
Them instead of focusing on the angle I focused on the point D. Either way will work of course.
So I got this to minimize (largest neg. value):
(for simplicity, let x=b1 from my diagram)
f(x) = sqrt(.16-x^2) + 1 - sqrt(-2x+1.16)
And my calculus is rusty but I could take the deriviative of f(x) but I think that f'(x) would be awful to solve symbolically. Of course we can plug f(x) into a numerical solver and get solutions, but that's not nearly as satisfying.
#3 Re: Help Me ! » HELP! Finding the slope in a word problem. » 2007-02-21 18:20:29
Since the problem is written
the the nearest hundred
we'd have to say that mathsyperson is technically right by saying zero.
But, being that we're human beings, we can detect that probably the problem probably meant to say
to the nearest hundredth
so pi man should have the intended answer.
best,
Kevin
#4 Help Me ! » Marquis De L'Hopital optimization problem » 2007-02-20 18:12:03
- fredekr
- Replies: 8
Can anybody outline a symbolic solution for the Marquis De L'Hopital optimization problem on this site?
It's at:
http://www.mathsisfun.com/marquis.html
I can solve it numerically in two different ways, but my analysis gives me a nasty relation that I didn't want to try to differentiate symbolically since it didn't look like it would be solvable.
best,
Kevin
#5 Re: Help Me ! » Remainder Theorem » 2007-02-20 18:09:19
Would it be correct to write it as:
A(x^2 - 1) + (Bx + C)/(x^2 - 1)
And then find the values of A, B and C? I know it's something like that.
Thanks for any help!
Jon.
No, that's not right. The Remainder Theorem tells you about roots and remainders. It looks to me like you're trying to divide polynomials (the first step in the applying the Remainder Theorem). For this problem, "long division" is the answer.
Try looking at this page:
http://www.purplemath.com/modules/polydiv3.htm
(look at the 2nd, 3rd, and 4th examples)
If that makes sense to you, great!
(If it doesn't it may be because you were taught a different division method in primary school -- US students are taught this method for basic division, but most European student are taught other techniques. If it doesn't makes sense, try searching on "long division" and do some simple problems with real numbers until you get the hang of the long division method when there's a remainder. Then go back to the polynomial division.)
cheers,
Kevin
Pages: 1