Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#1 2009-04-12 14:01:34
- serhat1_tr
- Member
- Registered: 2009-04-12
- Posts: 4
I need help for this chessboard question ?
On a standard chessboard how many different ways can you select a block of five neighbour squares?
Two squares are neighbours if they have a common side.
I try but I cant find if anyone solves this problem I ll be happy.
Thanks..
Offline
#2 2009-04-12 18:31:40
- JaneFairfax
- Member

- Registered: 2007-02-23
- Posts: 6,868
Re: I need help for this chessboard question ?
The blocks are called pentominoes. Put a particular pentomino in a particular orientation at the bottom-left corner of the chessboard, and see how far you can move to the right and how far up the board you can move. If you can move columns (counting the starting column) to the right and rows (counting the starting row) upwards, that means you can place that pentomino in that particular orientation in places on the board.
Now reflect and/or rotate the pentomino to give other orientations. If there are
different orientations altogether (including the orientation you started with) then you can place the piece ways on the board in any orientation.For example, consider this pentomino:
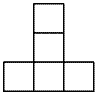
Place in on the bottom-left of the chessboard. Then you can move it
columns (counting the starting column) to the right before you hit the right edge of the board and rows (counting the starting row) upward before you reach the top edge. Hence there are ways of putting that piece in that orientation on the chessboard.There are three other orientations of that piece:
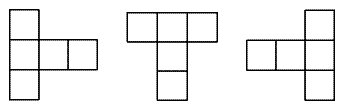
So there are 4 different orientations altogether. Hence the total number of ways of putting this pentomino in any orientation on the chessboard is
.There are 12 different pentomino shapes altogether. Do the same for each of them.
Last edited by JaneFairfax (2009-04-12 18:35:32)
Offline
#3 2009-04-12 23:38:06
- serhat1_tr
- Member
- Registered: 2009-04-12
- Posts: 4
Re: I need help for this chessboard question ?
Thanks ,
but if this table is 3x3 the answer is 49 so
when I solve on 8x8 I think 144 isnt the correct answer ??
Offline
#4 2009-04-12 23:47:54
- JaneFairfax
- Member

- Registered: 2007-02-23
- Posts: 6,868
Re: I need help for this chessboard question ?
Its 36 for each orientation, and 144 for all the four orientations.
Also, I was only showing you one pentomino example. There are other pentominoes you must check them all.

Last edited by JaneFairfax (2009-04-12 23:51:26)
Offline
#5 2009-04-12 23:53:12
- serhat1_tr
- Member
- Registered: 2009-04-12
- Posts: 4
Re: I need help for this chessboard question ?
jane can we talk on msn messenger ? this question is important for me . I have to solve it today
serhat1_tr[at]hotmail[dot]com
Offline
#6 2009-04-13 03:10:13
- serhat1_tr
- Member
- Registered: 2009-04-12
- Posts: 4
Re: I need help for this chessboard question ?
yeah I solve it 2308 ![]() Thanks Jane...
Thanks Jane...
Offline