Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#1 2012-03-16 12:25:12
- amberzak
- Member
- Registered: 2012-03-16
- Posts: 80
Geometric Progression?
I have been asked by my tutor to compile a GSP file investigating, what he called Geometric Progression. Basically, it's the thing where you get a polygon (say a square) and you direct it in a way that leads to a smaller version of the same polygon, which you keep repeating. I can't put a picture on to show you because I am a new member. And I don't know how to describe it. It creates a kind of spiral effect.
Well basically, I have been ask to find a relationship between the ratios of the area of the polygons, and the lengths of the sides too. I have created a table of results, but have been struggling to see a pattern. I can't even bring anything up on Google. I don't know what this is actually called.
Can anyone help me? I need to finish the work for Monday.
Thanks
Don't think outside the box. Think there is no box
Offline
#2 2012-03-16 12:26:16
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Geometric Progression?
Hi;
Post the table. It has been said that I can find a relationship between anything and anything else. Even when no such relationship exists.
Oh, and welcome to the forum.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#3 2012-03-16 12:31:35
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,808
Re: Geometric Progression?
hi amberzak,
Welcome to the forum.
Is this what you mean?
(hi bobbym. I'm glad you are on line for this one as I need to get some sleep. ![]() )
)
I'll check in again in about 8 hours.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#4 2012-03-16 21:46:30
- amberzak
- Member
- Registered: 2012-03-16
- Posts: 80
Re: Geometric Progression?
Bob. That's it.
Bobbym, I can't put my table up. It won't let me put images up yet. I'll try and write it.
Triangle dissected at a half - Area Ratio 4, Length ratio 2
Triangle dissected at a Third - Area ratio 3, Length ratio 1.73
Triangle Dissected at Quarter - Area ratio 2.29, Length Ratio 1.51
Triangle Dissected at a Fifth - Area Ratio 1.92, Length ratio 1.39
Square dissected at a half - Area Ratio 2, Length ratio 1.41
Square dissected at a Third - Area ratio 1.80, Length ratio 1.34
Square Dissected at Quarter - Area ratio 1.60, Length Ratio 1.26
Square Dissected at a Fifth - Area Ratio 1.47, Length ratio 1.21
Hexagon dissected at a half - Area Ratio 1.33, Length ratio 1.15
Hexagon dissected at a Third - Area ratio 1.29, Length ratio 1.13
Hexagon Dissected at Quarter - Area ratio 1.23, Length Ratio 1.11
Hexagon Dissected at a Fifth - Area Ratio 1.19, Length ratio 1.09
Sorry I didn't reply last night. I was so exhausted.
Thanks
Don't think outside the box. Think there is no box
Offline
#5 2012-03-16 23:28:20
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,808
Re: Geometric Progression?
hi amberzak,
When you get to 10 posts you'll stop being a 'novice' and become a 'member'. then you can post images, urls etc. This is to help prevent spammers from making one-off posts. Hope you understand.
So I'll look at the case for a square with dissection at 1/4.
So if your first square has a side length of 16, say, then the next 'loses' 1/4 so its side is 12 and the next is 9, and the next 27/4 ......
These form a geometric progression (GP):
16, 12, 9, 27/4, .....
The definition of a GP is that there is a constant ratio between one term and the next. Usually expressed as term(n+1) / term(n), so for your sequence, 12/16 = 9/12 = (27/4)/9 = 3/4 = r
I notice you've put 1.26. (i) Did you get this by measuring because I'd have expected 1.25 (one and a quarter). (ii) to write it in GP terms you need to use 3/4, I think.
Then next length = r x previous length eg. 3/4 x 9 = 27/4
The areas sequence is
256, 144, 81, (27/4)^2 = 45.5625, .....
These also make a GP:
144/256 = 81/144 = 45.5625/81 = 0.5625 which is 3/4 squared.
I think you will find these ratios occur for all polygons with a dissection of 1/4
You can learn more about GPs at
http://www.mathsisfun.com/algebra/seque … etric.html
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#6 2012-03-17 03:13:27
- amberzak
- Member
- Registered: 2012-03-16
- Posts: 80
Re: Geometric Progression?
I found the ratios by dividing the bigger area by the smaller area.
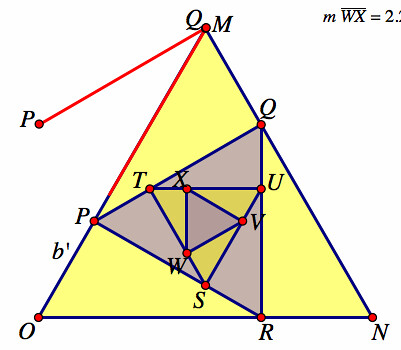
The picture below is an example of what I am doing. This is the triangle directed at half way along the edge The problem with what you are saying, bob, is that as you can see by the red line, the length of P-Q is more than 1 third and less than 2 thirds of the length. So it isn't as easy a ratio as you said.
THIS IS REALLY INFURIATING. I still can't post pictures, but I've done 10 posts.
I really need you to see it or it won't name any sense
Don't think outside the box. Think there is no box
Offline
#7 2012-03-17 03:14:46
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Geometric Progression?
Hi;
Can you paste the link here, please? Or is it a file on your computer?
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#8 2012-03-17 03:20:08
- amberzak
- Member
- Registered: 2012-03-16
- Posts: 80
Re: Geometric Progression?
I have the link. It most let me post it
Still keeps telling me I have to be a member to post links.
Don't think outside the box. Think there is no box
Offline
#9 2012-03-17 03:23:50
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Geometric Progression?
If you can not copy and paste the link then write it out using words. I will find the page and post it for you.
I have worked on the square problem and the way I am interpreting it means that it is far from easy. I have a solution but it requires some complex math to get at it. Here is my drawing:
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#10 2012-03-17 03:34:07
- amberzak
- Member
- Registered: 2012-03-16
- Posts: 80
Re: Geometric Progression?
Go onto flickr and search amberzakfilmsuk for people. It's the only photo on my page, and it's a triangle.
Don't think outside the box. Think there is no box
Offline
#11 2012-03-17 03:39:08
- amberzak
- Member
- Registered: 2012-03-16
- Posts: 80
Re: Geometric Progression?
It's sort of like that bob, except I have 4 versions of each shape, each one where the dividing spiralling is at the same distance - so one is always at the half way mark, the next is always a third of the way in etc. And it's Square, Triangle and Hexagon
The actual question stares What happens to the areas? (ratios)
What happens to the lengths of the sides?
Experiement with different starting polygons - do you always get the same ratios?
Maybe I'm making it more complicated than it has to be, and I don't need to find a link with each separate shape, only that within each shape the areas have the same ratios. But I am aiming for the top marks
Don't think outside the box. Think there is no box
Offline
#12 2012-03-17 03:41:54
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Geometric Progression?
Hi;
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#13 2012-03-17 03:44:05
- amberzak
- Member
- Registered: 2012-03-16
- Posts: 80
Re: Geometric Progression?
Yeah. That is the triangle I dissected at a third.
So you think you have the maths?
I don't even know how to google this to get some information on it. I know it's like fractals or something.
The red lines are just to show you that the lengths are not just cut, if you understand me
Last edited by amberzak (2012-03-17 03:45:12)
Don't think outside the box. Think there is no box
Offline
#14 2012-03-17 03:47:39
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Geometric Progression?
So you think you have the maths?
Sometimes I think I can cure a rainy day. But it is not raining...
I am not sure what you need but the answer I am getting is the Area of the triangles is
In other words it forms a geometric sequence with
so in simple talk the area of each triangle is 1 / 3 of the one before.
and the sides s also form a geometric sequence
so the sides form a geometric sequence with
meaning the sides of each triangle is 1 / √3 as big as the one before it.
Time for some rest, see you later.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#15 2012-03-17 05:39:38
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,808
Re: Geometric Progression?
hi amberzak,
By now you should be able to post pictures.
But you have to use the bottom right 'post reply' link. The 'quick reply' only allows basic text.
Anyway, I'm not sure I have your problem clear. Please take a look at my diagram below for equilateral triangles.
What is your rule for constructing DEF from ABC ?
It might help me if I had the exact wording of the original project from your tutor.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#16 2012-03-17 06:58:08
- amberzak
- Member
- Registered: 2012-03-16
- Posts: 80
Re: Geometric Progression?
The exact wording isn't very clear. It says
Take a reqular ploygon
Dissect it in a way that leads to a smaller version of the same polygon
Repeat with the new polygon - the process can go on for ever.
The then gave some examples, the picture bobby kindly posted for me (without the red lines) demonstrates his example.
Then he writes:
What happens to the areas (ratios?)
What happens to the lengths of the sides?
Experiment with different starting polygons - do you always get the same ratios?
That's it. All he wrote. I'm doing it on geometer's sketchpad (which isn't the easiest program to use doing this)
Thanks guys for all your help.
Bobby, how did you work out those figures? We've not actually been taught any of this.
Don't think outside the box. Think there is no box
Offline
#17 2012-03-17 11:17:16
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,808
Re: Geometric Progression?
hi amberzak
Great that you are on line too.
Stay on as I have some questions
Oh dear! While I was typing this you have logged off. Still I'll ask the first anyway in the next post.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#18 2012-03-17 11:22:16
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,808
Re: Geometric Progression?
Ok here's question number one.
How do you fix where D is on the line AB?
I'm getting the idea that you decide a fraction, say 1/2, and put D half way along.
Or (new fraction say 1/3) you put D 1/3 of the way along AB.
Once you have chosen the fraction, you make the next triangle in by putting 'G', lets call it, the same fraction along DE.
Is that right?
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#19 2012-03-17 13:55:09
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Geometric Progression?
Then he writes:
What happens to the areas (ratios?)
What happens to the lengths of the sides?
Experiment with different starting polygons - do you always get the same ratios?
Bobby, how did you work out those figures? We've not actually been taught any of this.
Your instructor wants you to experiment. He is not demanding rigor. How could he? You have not been taught this. I used geogebra. My work always looks like this:
Experiment -> Math -> Experiment -> Math -> Experiment ...
Your instructor is trying to get your mind working on math in an experimental way. He is probably not interested in another moldy, stuffy textbook proof already known to Euler.
Geometers sketchpad or geogebra are more than a match for this.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#20 2012-03-17 20:56:48
- amberzak
- Member
- Registered: 2012-03-16
- Posts: 80
Re: Geometric Progression?
Bob. I logged off just as you came on lol. I got too tired.
Yeah, that's how I worked it out. You have to keep the dividing fraction the same on each shape. So for example, on my first square I have kept it the same distance in fraction for every smaller square in that shape.
Oh, and bobby, thanks.
Last edited by amberzak (2012-03-17 20:57:08)
Don't think outside the box. Think there is no box
Offline
#21 2012-03-17 21:23:50
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,808
Re: Geometric Progression?
hi amberzak,
question 2: Why did you say anything about geometric progressions? Did he tell you that was where it leads or did you discover that?
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#22 2012-03-17 21:27:36
- amberzak
- Member
- Registered: 2012-03-16
- Posts: 80
Re: Geometric Progression?
He titled the work Geometric Progressions, but the assignment was given after a lesson on fractals.
Don't think outside the box. Think there is no box
Offline
#23 2012-03-17 21:33:10
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Geometric Progression?
Hi;
The successive triangles area and sides are in geometric progression.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#24 2012-03-17 21:40:00
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,808
Re: Geometric Progression?
hi amberzak
So you might reasonably expect this to lead to a GP.
As far as I can see it will when each polygon is a certain fraction of the one before.
But it won't happen if you reduce the length of a side by a fixed amount (say 1 cm) each time.
I've just used Sketchpad to make the diagram below.
First square 8 cm.
Find next four points by measuring in 1 cm from corners. (note. Second square has not got 7 cm sides!)
Then measure in 1 cm again and so on.
So this investigation could be taken in a new direction. That's when bobbym's comment becomes clearer. Two students could go different ways with this.
Have you spotted where you can use Pythagoras yet?
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#25 2012-03-17 21:46:17
- amberzak
- Member
- Registered: 2012-03-16
- Posts: 80
Re: Geometric Progression?
Yep. If I want to find the length of the new square: a^2+b^2 = c^2
I love pythagoras ![]()
All my other sketchpad work is already at the top mark, and they take our work as a whole (it's partly creating resources as well as finding out for ourselves) so I am thinking that maybe I shouldn't be trying to work out all the complex maths if I don't really have tim (it's due tomorrow and I have an essay due Tuesday).
That maybe I should just comment that it is in successive geometric progression and just give one example
Last edited by amberzak (2012-03-17 21:47:20)
Don't think outside the box. Think there is no box
Offline