Math Is Fun Forum

Keckman

Member

From: Helsinki Finland

Registered: 2022-12-13

Posts: 14

Website

Hypothetical question: what year do humans populate the universe?

Wild assumptions:
In one Universe there are 500 billion galaxies, each of which has 200 billion stars, of which every tenth has a planet that can be quite easily modified into a suitable place for humans to live, and the planet can hold an average of 10 billion people. At the moment, there is only one planet called Earth with life in that Universe.

Let's assume that the human population grows on average at the same rate as it has grown since 1700, when we were 640 million 35 thousand 774 about.

In this picture, the red curve describes when the number of people has multiplied by 1.0076 every year. The black curve is obtained based on actual values. That is, because that red curve "clicks" quite well with the real curve, the coefficient 1.0076 is used

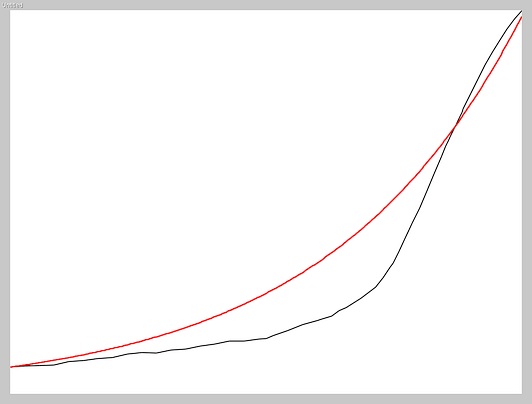
Question:
In what year do man populate the Universe, after which that 1.0076 multiplication per year must be adjusted to 1.0000 multiplication? The math problem  assumes, of course, that space travel is under control, and we can travel to distant stars and galaxies. This is a mathematical exercise and not a model of the real situation, as we currently have no way to travel to other stars and galaxies.

Solution: I don't know how to use logarithm calculation formulas now, but I solve the problem with a computer program: (maybe someone show me how this is done with logarithm?)

rebol[]
g: 5E+11 ;How Many galaxies?
g: (g * 2E+11) / 10 ;How many planets to populate
g: g * 1E+10 ; How many people there can be in Universe?
population: 640035774
year: 1700
until [
print [year " " population]
population: population * 1.0076
year: year + 1
population >= g
]
halt

Output:
1700   640035774
1701   644900045.8824
1702   649801286.231106
1703   654739776.006463
1704   659715798.304112
1705   664729638.371223
1706   669781583.622844
1707   674871923.658378
1708   680000950.278182
1709   685168957.500296
.
.
.
8743   9.2194892244472E+31
8744   9.289557342553E+31
8745   9.36015797835641E+31
8746   9.43129517899192E+31
8747   9.50297302235226E+31
8748   9.57519561732213E+31
8749   9.64796710401378E+31
8750   9.72129165400429E+31
8751   9.79517347057472E+31
8752   9.86961678895109E+31
8753   9.94462587654712E+31
>>

The answer is the year 8753. So pretty soon the entire universe will be populated! Right? Yes, exponential population growth is wild!