Orbit

Jai Ganesh · 2025-01-31 17:48:55

Orbit

Gist

An orbit is a regular, repeating path that one object in space takes around another one. An object in an orbit is called a satellite. A satellite can be natural, like Earth or the moon.

An orbit is a regular, repeating path that one object takes around another object or center of gravity. Orbiting objects, which are called satellites, include planets, moons, asteroids, and artificial devices. Objects orbit each other because of gravity.

MEO satellites have a relatively slower period of orbiting the Earth compared to LEO satellites. Geostationary Earth Orbit (GEO) At an altitude of 36,000 km, GEO orbit satellites have the main advantage of being able to stay over one point on the Earth's surface.

Low Earth orbit (LEO) encompasses Earth-centered orbits with an altitude of 1,200 miles (2,000 km) or less. This orbit is considered near enough to Earth for convenient transportation, communication, observation, and resupply.

A medium Earth orbit (MEO) is an Earth-centered orbit with an altitude above a low Earth orbit (LEO) and below a high Earth orbit (HEO) – between 2,000 and 35,786 km (1,243 and 22,236 mi) above sea level.

A highly elliptical orbit (HEO) is an elliptic orbit with high eccentricity, usually referring to one around Earth. Examples of inclined HEO orbits include Molniya orbits, named after the Molniya Soviet communication satellites which used them, and Tundra orbits. Molniya orbit for the Northern hemisphere.

Summary

An orbit is a regular, repeating path that one object in space takes around another one. An object in an orbit is called a satellite. A satellite can be natural, like Earth or the moon. Many planets have moons that orbit them. A satellite can also be man-made, like the International Space Station.

Planets, comets, asteroids and other objects in the solar system orbit the sun. Most of the objects orbiting the sun move along or close to an imaginary flat surface. This imaginary surface is called the ecliptic plane.

What Shape Is an Orbit?

Orbits come in different shapes. All orbits are elliptical, which means they are an ellipse, similar to an oval. For the planets, the orbits are almost circular. The orbits of comets have a different shape. They are highly eccentric or “squashed.” They look more like thin ellipses than circles.

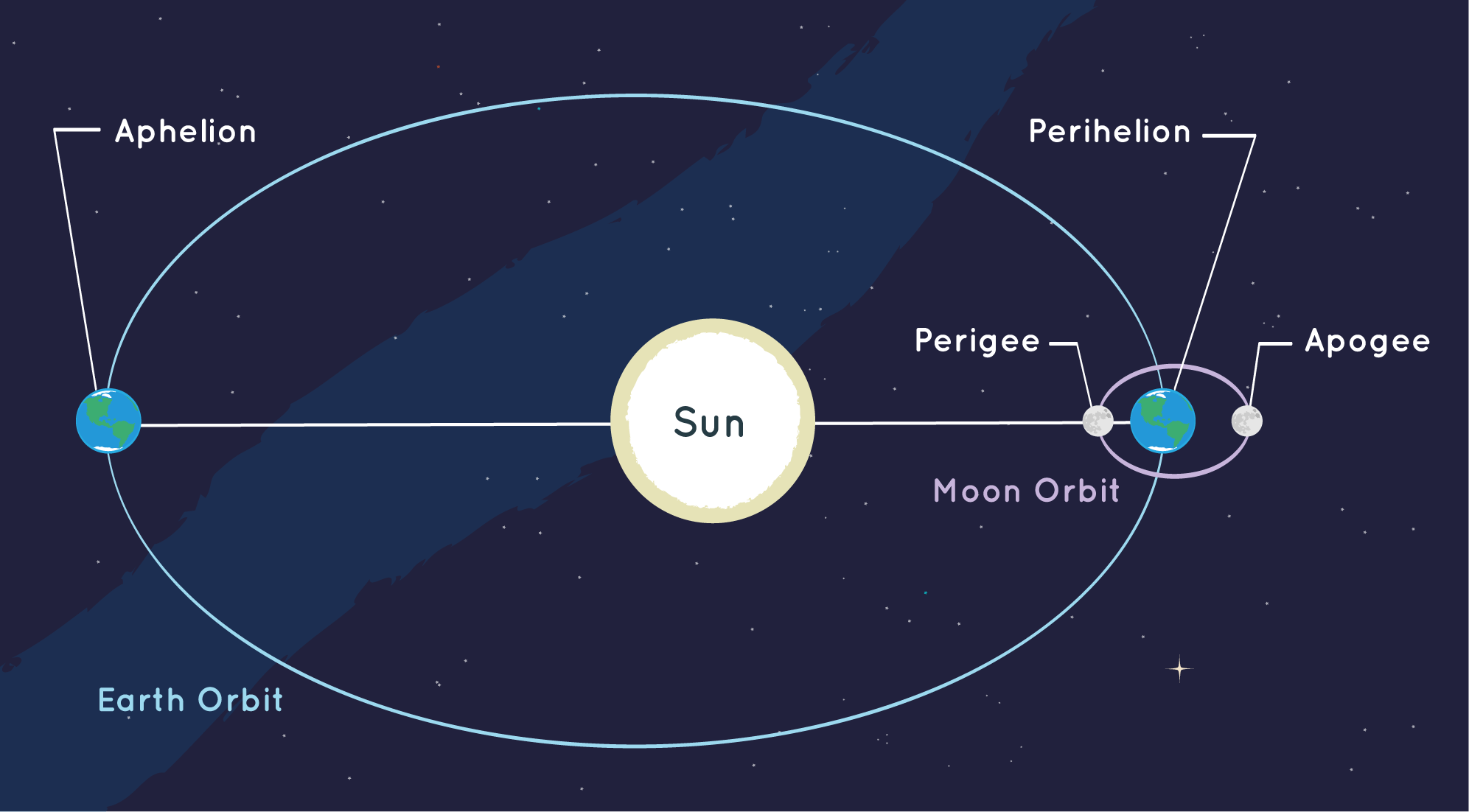
Satellites that orbit Earth, including the moon, do not always stay the same distance from Earth. Sometimes they are closer, and at other times they are farther away. The closest point a satellite comes to Earth is called its perigee. The farthest point is the apogee. For planets, the point in their orbit closest to the sun is perihelion. The farthest point is called aphelion. Earth reaches its aphelion during summer in the Northern Hemisphere. The time it takes a satellite to make one full orbit is called its period. For example, Earth has an orbital period of one year. The inclination is the angle the orbital plane makes when compared with Earth’s equator.

How Do Objects Stay in Orbit?

An object in motion will stay in motion unless something pushes or pulls on it. This statement is called Newton’s first law of motion. Without gravity, an Earth-orbiting satellite would go off into space along a straight line. With gravity, it is pulled back toward Earth. A constant tug-of-war takes place between the satellite’s tendency to move in a straight line, or momentum, and the tug of gravity pulling the satellite back.

An object’s momentum and the force of gravity have to be balanced for an orbit to happen. If the forward momentum of one object is too great, it will speed past and not enter into orbit. If momentum is too small, the object will be pulled down and crash. When these forces are balanced, the object is always falling toward the planet, but because it’s moving sideways fast enough, it never hits the planet. Orbital velocity is the speed needed to stay in orbit. At an altitude of 150 miles (242 kilometers) above Earth, orbital velocity is about 17,000 miles per hour. Satellites that have higher orbits have slower orbital velocities.

Where Do Satellites Orbit Earth?

The International Space Station is in low Earth orbit, or LEO. LEO is the first 100 to 200 miles (161 to 322 km) of space. LEO is the easiest orbit to get to and stay in. One complete orbit in LEO takes about 90 minutes.

Satellites that stay above a location on Earth are in geosynchronous Earth orbit, or GEO. These satellites orbit about 23,000 miles (37,015 km) above the equator and complete one revolution around Earth precisely every 24 hours. Satellites headed for GEO first go to an elliptical orbit with an apogee about 37,015 km. Firing the rocket engines at apogee then makes the orbit round. Geosynchronous orbits are also called geostationary.

Any satellite with an orbital path going over or near the poles maintains a polar orbit. Polar orbits are usually low Earth orbits. Eventually, Earth’s entire surface passes under a satellite in polar orbit. When a satellite orbits Earth, the path it takes makes an angle with the equator. This angle is called the inclination. A satellite that orbits parallel to the equator has a zero-degree orbital inclination. A satellite in a polar orbit has a 90-degree inclination.

Details

In celestial mechanics, an orbit (also known as orbital revolution) is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an object or position in space such as a planet, moon, asteroid, or Lagrange point. Normally, orbit refers to a regularly repeating trajectory, although it may also refer to a non-repeating trajectory. To a close approximation, planets and satellites follow elliptic orbits, with the center of mass being orbited at a focal point of the ellipse, as described by Kepler's laws of planetary motion.

For most situations, orbital motion is adequately approximated by Newtonian mechanics, which explains gravity as a force obeying an inverse-square law. However, Albert Einstein's general theory of relativity, which accounts for gravity as due to curvature of spacetime, with orbits following geodesics, provides a more accurate calculation and understanding of the exact mechanics of orbital motion.

History

Historically, the apparent motions of the planets were described by European and Arabic philosophers using the idea of celestial spheres. This model posited the existence of perfect moving spheres or rings to which the stars and planets were attached. It assumed the heavens were fixed apart from the motion of the spheres and was developed without any understanding of gravity. After the planets' motions were more accurately measured, theoretical mechanisms such as deferent and epicycles were added. Although the model was capable of reasonably accurately predicting the planets' positions in the sky, more and more epicycles were required as the measurements became more accurate, hence the model became increasingly unwieldy. Originally geocentric, it was modified by Copernicus to place the Sun at the centre to help simplify the model. The model was further challenged during the 16th century, as comets were observed traversing the spheres.

The basis for the modern understanding of orbits was first formulated by Johannes Kepler whose results are summarised in his three laws of planetary motion. First, he found that the orbits of the planets in our Solar System are elliptical, not circular (or epicyclic), as had previously been believed, and that the Sun is not located at the center of the orbits, but rather at one focus. Second, he found that the orbital speed of each planet is not constant, as had previously been thought, but rather that the speed depends on the planet's distance from the Sun. Third, Kepler found a universal relationship between the orbital properties of all the planets orbiting the Sun. For the planets, the cubes of their distances from the Sun are proportional to the squares of their orbital periods. Jupiter and Venus, for example, are respectively about 5.2 and 0.723 AU distant from the Sun, their orbital periods respectively about 11.86 and 0.615 years. The proportionality is seen by the fact that the ratio for Jupiter, {5.23}^{3}/{11.862}^2, is practically equal to that for Venus, {0.7233}^{3}/{0.6152}^2, in accord with the relationship. Idealised orbits meeting these rules are known as Kepler orbits.

Isaac Newton demonstrated that Kepler's laws were derivable from his theory of gravitation and that, in general, the orbits of bodies subject to gravity were conic sections (this assumes that the force of gravity propagates instantaneously). Newton showed that, for a pair of bodies, the orbits' sizes are in inverse proportion to their masses, and that those bodies orbit their common center of mass. Where one body is much more massive than the other (as is the case of an artificial satellite orbiting a planet), it is a convenient approximation to take the center of mass as coinciding with the center of the more massive body.

Advances in Newtonian mechanics were then used to explore variations from the simple assumptions behind Kepler orbits, such as the perturbations due to other bodies, or the impact of spheroidal rather than spherical bodies. Joseph-Louis Lagrange developed a new approach to Newtonian mechanics emphasizing energy more than force, and made progress on the three-body problem, discovering the Lagrangian points. In a dramatic vindication of classical mechanics, in 1846 Urbain Le Verrier was able to predict the position of Neptune based on unexplained perturbations in the orbit of Uranus.

Albert Einstein in his 1916 paper The Foundation of the General Theory of Relativity explained that gravity was due to curvature of space-time and removed Newton's assumption that changes in gravity propagate instantaneously. This led astronomers to recognize that Newtonian mechanics did not provide the highest accuracy in understanding orbits. In relativity theory, orbits follow geodesic trajectories which are usually approximated very well by the Newtonian predictions (except where there are very strong gravity fields and very high speeds) but the differences are measurable. Essentially all the experimental evidence that can distinguish between the theories agrees with relativity theory to within experimental measurement accuracy. The original vindication of general relativity is that it was able to account for the remaining unexplained amount in precession of Mercury's perihelion first noted by Le Verrier. However, Newton's solution is still used for most short term purposes since it is significantly easier to use and sufficiently accurate.

Planetary orbits

Within a planetary system, planets, dwarf planets, asteroids and other minor planets, comets, and space debris orbit the system's barycenter in elliptical orbits. A comet in a parabolic or hyperbolic orbit about a barycenter is not gravitationally bound to the star and therefore is not considered part of the star's planetary system. Bodies that are gravitationally bound to one of the planets in a planetary system, either natural or artificial satellites, follow orbits about a barycenter near or within that planet.

Owing to mutual gravitational perturbations, the eccentricities of the planetary orbits vary over time. Mercury, the smallest planet in the Solar System, has the most eccentric orbit. At the present epoch, Mars has the next largest eccentricity while the smallest orbital eccentricities are seen with Venus and Neptune.

As two objects orbit each other, the periapsis is that point at which the two objects are closest to each other and the apoapsis is that point at which they are the farthest. (More specific terms are used for specific bodies. For example, perigee and apogee are the lowest and highest parts of an orbit around Earth, while perihelion and aphelion are the closest and farthest points of an orbit around the Sun.)

In the case of planets orbiting a star, the mass of the star and all its satellites are calculated to be at a single point called the barycenter. The paths of all the star's satellites are elliptical orbits about that barycenter. Each satellite in that system will have its own elliptical orbit with the barycenter at one focal point of that ellipse. At any point along its orbit, any satellite will have a certain value of kinetic and potential energy with respect to the barycenter, and the sum of those two energies is a constant value at every point along its orbit. As a result, as a planet approaches periapsis, the planet will increase in speed as its potential energy decreases; as a planet approaches apoapsis, its velocity will decrease as its potential energy increases.

Additional Information

Orbit, in astronomy, is the path of a body revolving around an attracting centre of mass, as a planet around the Sun or a satellite around a planet. In the 17th century, Johannes Kepler and Isaac Newton discovered the basic physical laws governing orbits; in the 20th century, Albert Einstein’s general theory of relativity supplied a more exact description.

The orbit of a planet is, if unaffected by the attraction of another planet, elliptical; some elliptical orbits are very nearly circles, while others are much elongated. Some bodies may follow parabolic or hyperbolic paths (open-ended curves). The orbit of a body approaching the solar system from a very great distance, curving once around the Sun, and receding again is such an open curve.

In determining the elements of a body’s orbit, at least three positions of the body should be measured. Observations should be spread evenly in time and should extend over a considerable arc of the orbit. Further measurements are necessary to account for the effects of minor disturbing forces, such as planetary attractions, irregularities of mass within the body at the centre of the orbit, and, in the case of some artificial satellites, atmospheric drag.

An orbit is completely described by six geometric properties called its elements; from them the future positions of the planet can be calculated. The elements are (1) the inclination of the orbit plane and (2) the longitude of the ascending node, which fix the orbit plane; (3) the semimajor axis, (4) the eccentricity and (5) the longitude of periapsis (see apse), which fix the size and shape of the orbit in the orbit plane; and (6) the time of periapsis, which locates the body in the orbit. These are explained below.

The Sun occupies one of the two foci of the ellipse of a planet’s orbit. A line drawn through the point of the planet’s closest approach to the Sun (perihelion) and farthest retreat (aphelion) passes through the Sun and is called the line of apsides or major axis of the orbit; one-half this line’s length is the semimajor axis, equivalent to the planet’s mean distance from the Sun. The eccentricity of an elliptical orbit is a measure of the amount by which it deviates from a circle; it is found by dividing the distance between the focal points of the ellipse by the length of the major axis. To predict the position of the planet at any time it is necessary to know the time when it passed through any definite position; e.g., its time of perihelion passage.

The inclination, or tilt, of a planet’s orbit is measured in degrees of arc from the plane of Earth’s orbit, called the ecliptic. S, at the centre of the drawing, represents the Sun. The points where the two orbital planes intersect (as projected in imagination upon the celestial sphere) are called the nodes, shown as M and N. V is the vernal equinox, a point on the ecliptic from which several celestial coordinates are measured. The angle VSN, in degrees of arc, is the longitude of the ascending node, i.e., of the point where the moving planet passes north of the plane of Earth’s orbit. M, the descending node, is where the planet passes from north to south. The sum of the angles subtended at S by the arcs VN and NA is called the longitude of the perihelion. It defines the direction of the major axis in the plane of the orbit.

orbit.en.png

Math Is Fun Forum

#1 2025-01-31 17:48:55

Orbit

Board footer