Coordinate Geometry Formulas

MathsIsFun · 2006-03-29 10:06:28

Jai Ganesh · 2006-04-01 18:48:57

Straight line

y = mx + c where m is the slope.
The slope or gradient m of a straight line is tan of the angle made with the positive x-axis.

The slopes of two parallel lines, m1 and m2 are equal if the lines are parallel. If the two lines are perpendicular, m1*m2=-1.

Finding the y-intercept:- Put x=0, In the above equation, c is the y-intercept.
Finding the x-intercept:- Put y=0. In the above equation, -c/m is the x-intercept.

Equation of a straight line parallel to the y-axis at a distance 'a' from it is x=a.

Equation of a straight line parallel to the x-axis at a distance 'b' from it is y=b.

Equation of a line parallel to the x-axis and passing throught the point (a,b) is y=b.

Equation of a line perpendicular to x-axis and passing through (a,b) is x=a.

Equation of a line parallel to the y-axis and passing through (a,b) is x=a.

Equation of a line perpendicular to the y-axis and passing through (a,b) is y=b.

Equation of x-axis is y=0 and equation of y-axis is x=0.

The equation of a straight line which cuts off intercepts a and b on the x-axis and y-axis is x/a+y/b=1.

The equation of a staright line passing through the origin (0,0) is y=mx.

The equation of a straight line passing through the origin and making equal angle with both the axes is y=±x

One point form:-

where m is the slope of the straight line and it passes through the point

Slope of a line passing through

is given by

The equation of a straight line passing through

is given by

Jai Ganesh · 2006-04-08 18:42:40

Distance between two points.

The distance between two points

and is given by

The distance of a point (x,y) from the origin is given by

Jai Ganesh · 2006-04-08 19:29:20

Section formula

The point which divides the line joining two points

in the ratio m:n internally is

The point which divides the line joining two points

in the ratio m:n externally is

The point which bisects the line joining two points

is

Area of a triangle

The area of the triangle formed by the three points

is given by

.

The three points are collinear if the area of the triangle formed is zero.

If the three vertices of a triangle are

Coordinates of the Cetroid:- (The meeting pint of the three medians)

If for the above said triangle, the lengths of the three sides of the triangle are a,b, and c,
Cordinates of the Incentre:- (The centre of a circle which touches the sides of a triangle, also the point of interesction of the angle bisectors of the triangle)

Jai Ganesh · 2006-04-15 03:37:07

Concurrent lines
If the lines

are concurrent, then

Angle between two lines

Let the two lines

make angles
with the positive x axis. Then,
.

The angle between the lines is given by

For parallel lines,

and for perpendicular lines,

The angle between the lines

is given by

If the lines are parallel,

.

If the lines are perpendicular to each other,

Perpendicular distance from origin
The perpendicular distance from the origin to the line ax+by+c=0 is

Perpendicular distance of a line from a point

The perpendicular distance from the point

to the line ax+by+c=0 is given by

Jai Ganesh · 2006-04-15 19:05:44

Circle

The equation of a circle whose center is (h,k) and radius is a is given by the equation

The equation of a circle whose centre is the origin and whose radius is a is given by the equation

The general equation of a circle is

where the centre is (-g,-f) and radius is

The equation of a circle whose one diameter is the line segment joining the points

is given by

The equation

represents

a real circle if

a point circle (a circle of zero radius) if

and an imaginary circle if

Jai Ganesh · 2006-04-21 21:58:32

Circle through three points

Given three points

the equation of the circle passing through the three points is

Jai Ganesh · 2006-05-10 03:41:39

Area of a Quadrilateral

The area of a quadrilateral whose vertices are

is given by

Jai Ganesh · 2006-05-13 02:42:42

Conics

A conic is defined as the locus of a point which moves such that its distance from a fixed point is always e times its distance from a fixed straight line. The fixed point is called the focus of the conic and the fixed straight line is called the directrix of the conic. The constant ratio, e, is called the eccentricity of the conic.
If e<1, the conic is a parabola. If e=1, the conic is an ellipse and if e>1, the conic is a hyperbola.

Parabola

Standard form of a parabola:-

The coordinates of the focus are (a,0) and the vertex of the parabola is (0,0), the curve is symmetric about the x-axis.

Equation of the tangent at (x1, y1)

Condition that y=mx+c may be a tangent:-

The point of contact is

Latus rectum = 4a

Eccentricity, e=1

Equation of directrix, x=-e.

Equation of normal at (x1, y1):-

Equation of chord of contact of tangents drawn from (x1,y1):-

Parametric Representation

The coordinates (at², 2at) satisfies the equation y²=4ax.

The equation of the chord joining the points t1 and t2 on the parabola y²=4ax is

The equation of the tangent at (at², 2at) is

The equation of the normal at (at², 2at) is

The point of intersection of tangents at t1 and t2 is

Ellipse

Standrad form:-

The coordinates of the foci are (ae, 0) and (-ae, 0).
Tangent at (x1,y1)

Condition that y=mx+c may be a tangent:-

Latus rectum :

Eccentricity,

Equation of directrices:-

Equation of normal at (x1, y1):-

Equation of chord of contact of tangents drawn from (x1, y1):

Parametric Representation

x=acosθ, y=bsinθ satisifies the equation of the ellipse.

The equation of the tangent at θ is

The equation of normal at θ is

Hyperbola

Standard form:-

Tangent at (x1, y1):-

Condition that y=mx+c may be a tangent:-

Latus rectum :-

Eccentricity, e

Equation of directrices:-

Equation of normal at (x1, y1):-

Equation of chord of contact of tangents drawn from (x1,y1):-

An asymptote of a hyperbola is a straight line which touches the hyperbola at infinity but does not lie altogether at infinity.

The equations of asymptotes of a hyperbola are

Parametric Representation

x=asecθ, y=btanθ satisifies the equation of the hyperbola.

The equation of the tangent at θ is

The equation of the normal at θ is

Rectangular Hyperbola

A hyperbola in which b=a is called a Rectangular hyperbola. The asymptotes of a rectangular hyperbola are at right angles to each other.
The asymptotes of a Rectangular Hyperbola are

Standard form:-

Tangent at (x1, y1):-

Latus rectum = 2a

Eccentricity, e= √2

Equation of normal at (x1, y1):-

Equation of chord of contact of tangents drawn from (x1, y1):-

Parametric form

The point

satisifes the equation of the rectangular hyperbola,

The equation of the tangent at t is

The equation of the normal at t is

Jai Ganesh · 2006-05-18 02:47:02

Equation of a plane

The equation of a plane passing through three non-collinear points having coordinates (x1,y1,z1), (x2,y2,z2), and (x3,y3,z3) can be dtermined by the following determinant equations:

Jai Ganesh · 2006-06-10 02:35:00

Angle between two planes

Let the equations of two planes be
ax+by+cz+d=0 and
a1x+b1y+c1z+d1=0

The angle between the two planes is defined as the angle between the normals.

If θ is the angle between the normals, then

Jai Ganesh · 2006-06-10 03:02:13

Perpendicular distance from a point to a plane

The perpendicular distance of the point (x1, y1, z1) from the plane
Ax+By+Cz+D=0 is given by

The perpendicular distance from the origin to the plane
Ax+By+Cz+D=0 is

Zhylliolom · 2006-08-05 14:08:36

Translation of Axes

The coordinates (x', y') of a coordinate system with origin O' = (x[sub]0[/sub], y[sub]0[/sub]) relative to the standard origin (0, 0) are related to the standard (x, y) coordinates by the transformation equations

or

Rotation of Axes

The coordinates (x', y') of a coordinate system with origin (0, 0) with the x'-axis making an angle of α with the positive x-axis are related to the standard (x, y) coordinates by the transformation equations

or

Translation and Rotation of Axes

The coordinates (x', y') of a coordinate system with origin O' = (x[sub]0[/sub], y[sub]0[/sub]) relative to the standard origin (0, 0) and with the x'-axis making an angle of α with the positive x-axis are related to the standard (x, y) coordinates by the transformation equations

or

Zhylliolom · 2006-08-06 09:25:07

Polar Coordinates

The transformation equations relating rectangular coordinates (x, y) and polar coordinates (r, θ) are

or

Listing of Several Types of Polar Curves

Use the Polar Grapher to graph these curves.

Circle

The equation for a circle of radius r[sub]0[/sub] centered at the origin is given by

If the circle is centered at (c, α) and has radius r[sub]0[/sub], its equation is

Ellipse

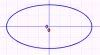
The equation of an ellipse of semi-major axis a and semi-minor axis b centered at the origin is given by

Parabola

If the distance from the vertex to the focus of a parabola is a, then its equation is

Hyperbola

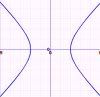
The equation of a hyperbola of semi-major axis a and semi-minor axis b centered at the origin is given by

Lemniscate

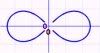
The equation of a lemniscate in polar coordinates is

In rectangular coordinates this is

The area inside both loops of the lemniscate is

Cardioid

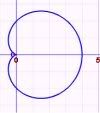
The equation of a cardioid is given by

The area of the cardioid is

and its perimeter is

Three-Leaved Rose

The equation of a three-leaved rose is

For odd n, r = a cos nθ and r = a sin nθ are n-leaved roses.

Four-Leaved Rose

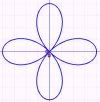
The equation of a four-leaved rose is

For even n, r = a cos nθ and r = a sin nθ are 2n-leaved roses.

Limaçon

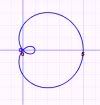
The equation of a limaçon is

Spiral of Archimedes

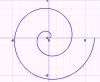
The equation of a spiral of Archimedes is

Last edited by Zhylliolom (2006-08-06 10:06:23)

Identity · 2007-08-11 23:14:40

Turning point of a parabola of the form y=ax² +bx+c

or...

Last edited by Identity (2007-08-11 23:15:59)

Math Is Fun Forum

#1 2006-03-29 10:06:28

Coordinate Geometry Formulas

#2 2006-04-01 18:48:57

Re: Coordinate Geometry Formulas

#3 2006-04-08 18:42:40

Re: Coordinate Geometry Formulas

#4 2006-04-08 19:29:20

Re: Coordinate Geometry Formulas

#5 2006-04-15 03:37:07

Re: Coordinate Geometry Formulas

#6 2006-04-15 19:05:44

Re: Coordinate Geometry Formulas

#7 2006-04-21 21:58:32

Re: Coordinate Geometry Formulas

#8 2006-05-10 03:41:39

Re: Coordinate Geometry Formulas

#9 2006-05-13 02:42:42

Re: Coordinate Geometry Formulas

#10 2006-05-18 02:47:02

Re: Coordinate Geometry Formulas

#11 2006-06-10 02:35:00

Re: Coordinate Geometry Formulas

#12 2006-06-10 03:02:13

Re: Coordinate Geometry Formulas

#13 2006-08-05 14:08:36

Re: Coordinate Geometry Formulas

#14 2006-08-06 09:25:07

Re: Coordinate Geometry Formulas

#15 2007-08-11 23:14:40

Re: Coordinate Geometry Formulas

Board footer