Theorem of pappus and the integral of e^(x^2) dx

mikau · 2007-03-28 10:19:30

You cannot find the area under the curve e^(x^2) dx in terms of a simple elementary function. But you CAN find the volume if you revolve this region about the y axis. This has always intrigued me. "Surely!" I thought "If you can find the volume of that region you should be able to find the area through some manipulation of the volume." while that has prooved to be untrue, I've done a lot of thinking in that area. Given that the the integral of e^(x^2) dx is a non elementary function, we cannot expect to figure it out as a simple function. But if we could perhaps express it as a fairly complicated limit that cannot be expressed as an elementary function, perhaps one could find fairly accurate summations by plugging super small or big values into the limit. (this is why I posted a question in the help forum about nonelementary functions and limits)

Anyway, I've been messing around with the problem for a while, and managed to come up with something that might be interesting to some of you. I came up with a limit involving the quadratic formula. I wrote a java program to do manual integration (so to speak) using 1 million approximating rectangles, and also to evaluate my limit. Here is a table comparing the results of my limit to the results of one million approximating rectangles. I will refer to the 1 million rectangle approximation as the "actual area" and the limit I found as "my approximation"

The area under e^(x^2) from 0 to 2:

My approximation: 16.6694160595025
actual area: 16.45257416743001

YIKES! Thats fairly close!

The area from 0 to 3:
My approximation: 1442.2309461750158
actual area: 1444.5329698033047

Thats also pretty close.

The area from 0 to 4.
My approximation: 1149236.6711155705
actual area: 1149382.8624656822

Uh...thats relatively close, but not exactly perfect.

As you can see, the approximation appears to be getting increasingly innacurate. Furthermore, punching in smaller and smaller values for the limit usually don't effect it too much until you appearently reach java's limits for calculation accuracy and the values spiral out of control. The limit seems to consistently converge to a nearby, but imperfect approximation. That being the case, it cannot be denied there is an eerie similarity between the actual area, and the limit.

Now there are a lot of unknowns here because the accuracy of the variables in java may be playing a role. Also the amount of number crunching required to calculate the limit may be more time consuming then appproximating rectangles, plus at only 0 to 4 the approximation appears to be over 100 units off, meaning it would probably be completely off if we considered a much larger region. However, while I'm certainly not convinced the limit I found does in fact converge to the correct area, I cannot reject that possibility due to the striking resemblence between the digits.

Anyways, now I'll tell you where I got this limit from.

For those who aren't familiar with the theorem of Pappus, pappus discovered that the volume of a solid of revolution is equal to the area of the region, multiplied by the distance the centroid travels as the region is revolved. (centroid meaning the center of gravity) if we revolve the region y= e^(x^2) about the y axis, this volume (which we can find) is equal to the area of the region (which we don't know) times the x coordinate of the regions center of gravity, or centroid. (which we also can't find.)

We know that we can find the x coordinate of the centroid of f(x) on [a, b] as the integral of x*f(x) dx from a to b, divided by the the integral of f(x) from a to b. The numerator, in this case, we can find, the denominator we cannot find.

Consider the volume of the solid of revolution if you revolve the region from a to b about the y axis. This volume, (which I'll call V1) we can find using integration. But we also know it is equal to the area of the region "A" times 2pi times the x coordinate of the centroid, (which I'll call c)

V1 = 2pi*c*A. (A = integral of e^(x^2) dx from a to b)

Now here's where my idea kicks in. If we consider the region from a to b+h, we can still find the exact volume of this solid by integrating. However, using the theorem of pappus, we can see that:

V2 = 2pi*(c + Δc)*(A + ΔA)

We can easily find the change in the area as you add one sliver. We are given that c is computable as a ratio of two integrals, therefore by differentiating, we can find the change in the centroid vs the change in x. In otherwords, dc vs dx. What you end up with when you do this, is a new fraction involving A. This fraction contains A in the numerator and A^2 in the denominator. If, in equation 2, you replace Δc with this new expression related to Δx, solve for c and subsitute that in equation 2 as well, and you end up with a quadratic equation involving A and Δx. If you solve this rather lengthy quadratic equation, and plug it into the quadratic equation you get the limit I came up with. I won't bother to show the exact values I found unless someone wants them.

Anyways. The problem both fascinates and baffles me. Some things just don't make any sense at all. The fact that the limit consistently converges relatively close to the actual area is encouraging, however the limit refuses to be 100% correct most of the time. Its also picky. For instance, calculating the area of the added sliver I mentioned. Using Δx*f(b) or Δx*f(b + Δx) provides an approximation that is no where near the actual area. But considering the region as the trapazoid that it is (namely, Δx*f(x + Δx/2)) the limit suddenly jumps dangerously close.

Anyways, what this basically allows you to do is find the integral of f(x) by considering only the integral of x*f(x) dx and then solving for the integral in terms of a limit. That being said, I was able to find the area under the curve y = x^2 from 0 to 2 by considering the integral of x^3 and ended up with 2.66666... which IS the correct area in that case. But again, its just too independable to be sure.

A lot of what I'm finding, seems almost contradictory to what I know, or thought I knew, of limits, and of calculus. I keep telling myself that I'm completely off track but when I look at how close my approximation is, I know I must be doing something right. Or almost right at least.

Anyways, I believe I may have reached the limit of my current ability (pun intended) and thought maybe it was time to discuss it with someone more capable.

Last edited by mikau (2007-03-28 10:29:21)

mikau · 2007-03-28 11:04:25

Here's a diagram to help illustrate what I'm doing.

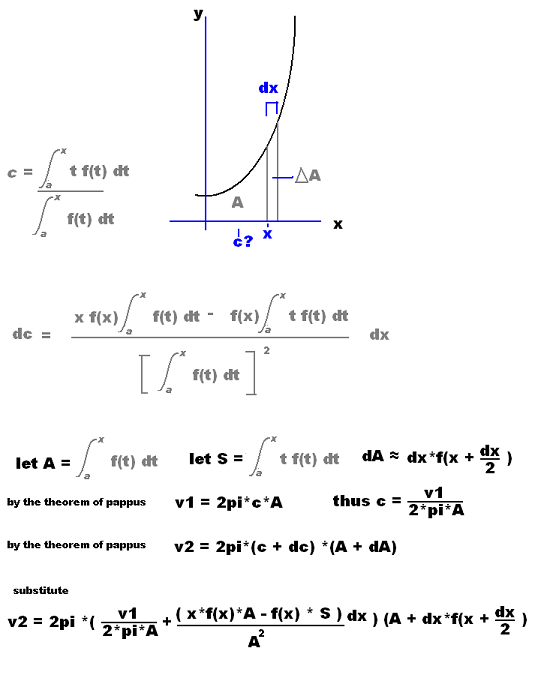
Remember that V1 and V2 are each a volume of a solid of revolution who's values we CAN find. Also note we can find the value of S. The result is an expression involving known values, dx, and A. With a bit of rearranging you can rewrite this as a quadratic equation and solve for A. The quadratic formula gives you a value of A dependant on dx. I obtained the approximitions I posted by making dx super super small and evaluating the quadratic formula. The interesting thing is that a limit does appear to be reached and is always fairly close to the actual area.

Last edited by mikau (2007-03-28 11:06:30)

mikau · 2007-03-29 02:14:55

No one has any comments to make?

John E. Franklin · 2007-04-12 05:02:30

I am really inspired by your self-study, learning calculus by self, and continuing like this. I'm way behind you in this subject, but perhaps a decade will come when I beef up on calculus. When I finally do that, I realize it will be a grand effort, as I've been through many courses in the past, but never really got the knack of it.

mikau · 2007-04-13 01:41:43

lol. Well I'm not sure if I've got the knack of it either. Treating differentials correctly can be really confusing at times.

This topic baffles the heck out of me. I appear to have developed a relatively accurate method of approximation, but I can't see why. I expected either 100%or completely off. Very peculiar this is.

majik1213 · 2007-04-27 10:03:02

"You cannot find the area under the curve e^(x^2) dx in terms of a simple elementary function. "

The area under the curve e^x^2 equals [SUM(FROM_n=0_TO_n=INFINITY) OF {(x^(2n+1))/((2n+1)(n!))} MINUS SUM(FROM_n=0_TO_n=INFINITY) OF {(a^(2n+1))/((2n+1)(n!))}] for all x greeater than or equal to a. This equation, derived from the formal definition of e (via a taylor series expansion), is impossible to evaluate predcisely because you have to keep adding terms forever. In practice, a finite limit on n is necessary. You can get good results by expressing the summation recursively, and then forcing the ratio of the n+1 coefficient over the n coefficient equal to zero for some n.

Hope this helps. I apologize in advance if I did not successfully adress the topic of your question. I am especially hesitant to talk as though I know the solution because I am uncertain to what a simple elementary function is. Could you give an example of a simple function that is not elementary, and an elementary function that is not simple? I should look these things up before posting, yes, yes, but the examples would help. If you were to try to apply the aforementioned equation in your java script application, via recursive relation formulas, I'm sure you'd get some good results.

Also ..

For those who aren't familiar with the theorem of Pappus, pappus discovered that the volume of a solid of revolution is equal to the area of the region, multiplied by the distance the centroid travels as the region is revolved. (centroid meaning the center of gravity) if we revolve the region y= e^(x^2) about the y axis, this volume (which we can find) is equal to the area of the region (which we don't know) times the x coordinate of the regions center of gravity, or centroid. (which we also can't find.)

If a=-x, then the centroid of the x-coordinate is 0. Otherwise, the x-coordinate, as you say, cannot be determined; however, I would venture to say the x-coordinate centroid equals positive infinity (domain of integration: FROM_0_TO_POSITIVE.INFINITY along the x-axis), because you must at least be certain that the x-coordinate centroid is not finite, for if you were to pick a point that you thought was a finite x-coordinate centroid, then I'd elongate the domain of 0 to n (along the x-axis) even farther, ever so far as to continue to push the x-centroid into an infinite region.

Last edited by majik1213 (2007-04-27 10:32:09)

Math Is Fun Forum

#1 2007-03-28 10:19:30

Theorem of pappus and the integral of e^(x^2) dx

#2 2007-03-28 11:04:25

Re: Theorem of pappus and the integral of e^(x^2) dx

#3 2007-03-29 02:14:55

Re: Theorem of pappus and the integral of e^(x^2) dx

#4 2007-04-12 05:02:30

Re: Theorem of pappus and the integral of e^(x^2) dx

#5 2007-04-13 01:41:43

Re: Theorem of pappus and the integral of e^(x^2) dx

#6 2007-04-27 10:03:02

Re: Theorem of pappus and the integral of e^(x^2) dx

Board footer