Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2009-04-02 07:25:10
- ben
- Member
- Registered: 2006-07-12
- Posts: 106
Push-me, pull you
This is so much fun! Look
We will suppose that
are vector spaces, and that the linear operators (aka transformations) . Then we know that the composition as shown here.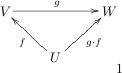
Notice the rudimentary (but critical) fact, that this only makes sense because the codomain of
is the domain ofNow, it is a classical result from operator theory that the set of all operators
is a vector space (you can take my word for it, or try to argue it for yourself).Let's call the vector space of all such operators
etc. Then I will have that are vectors in these spaces.The question naturally arises: what are the linear operators that act on these spaces? Specifically, what is the operator that maps
onto ?By noticing that here the
is a fixed domain, and that , we may suggest the notation . But, for reasons which I hope to make clear, I will use a perfectly standard alternative notation .Now, looking up at my diagram, I can think of this as "pushing" the tip of the f-arrow along the g-arrow to become the composite arrow. Accordingly, I will call this the push-forward of
on , or, by a horrid abuse of English as we normally understand it, the push-forward ofSo, no real shocks here, right? Ah, just wait, the fun is yet to begin, but this post is already over-long, so I'll leave you to digest this for a while.........
Offline
#2 2009-04-03 09:22:08
- ben
- Member
- Registered: 2006-07-12
- Posts: 106
Re: Push-me, pull you
Recall that, given
as a linear operator on vector spaces, we found as the linear operator that maps onto , and called it the push-forward of . In fact let's make that a definition: defines the push-forward.This construction arose because we were treating the space
as a fixed domain. We are, of course, free to treat as as fixed codomain, like this.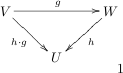
This seems to make sense, certainly domains and codomains come into register correctly, and we easily see that .
Using our earlier result, we might try to write the operator
, but something looks wrong; is going "backwards"!Nothing daunted, let's adopt the convention
. (We will see this choice is no accident)Looking up at my diagram, I can picture this a pulling the "tail" of the h-arrow back along the g-arrow onto the composite arrow, and accordingly (using the same linguistic laxity as before), call
the pull-back of , and make the definition: defines the pullback(Compare with the pushforward)
This looks weird, right? But it all makes beautiful sense when we consider the following special case of the above.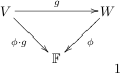
where I have assumed that
Putting this all together I find that, for
I will have as my pullback.I say this is just about as nice as it possibly could be. What say you?
Offline
Pages: 1