Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#1 2005-10-16 11:30:42
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
My 3D engine: reinventing the wheel
I've just finished trig and moving onto calculus. I've only learned a little C++ but for practice I decided to write my own program for practice in math and programming.
I have not been taught how a 3d engine works, mathematically. I found this explanation here http://en.wikipedia.org/wiki/3D_projection but I guess I'm not quite at the level needed to understand it. So I decided to see if I could figure out my own. Basicly I'm reinventing the wheel trying to figure things out myself, for the fun of it, to see how smart I am. lol. My engine is not even close to a real 3d engine yet since all it does is translate mathematical points based on distance, angle, etc. I'll try to post some step by step pics of how the program works.
A logarithm is just a misspelled algorithm.
Offline
#2 2005-10-16 12:36:15
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
Ok, what we want to do basicly in a 3d engine is convert 3d, to 2d. We are creating an illusion to graph 3d objects on a 2d plane (a computer or tv screen) so that they appear to be three dimensional even though its being displayed on a flat surface.
A computer screen is supposed to be like a window to a world. If you were to look through a window at a box, the image of the box would be passing through the window at a certain point and entering your eyes. If you were to replace the window with a board and draw the box at the exact same place where the original box passed through the glass, it would look just like the real box through the window.
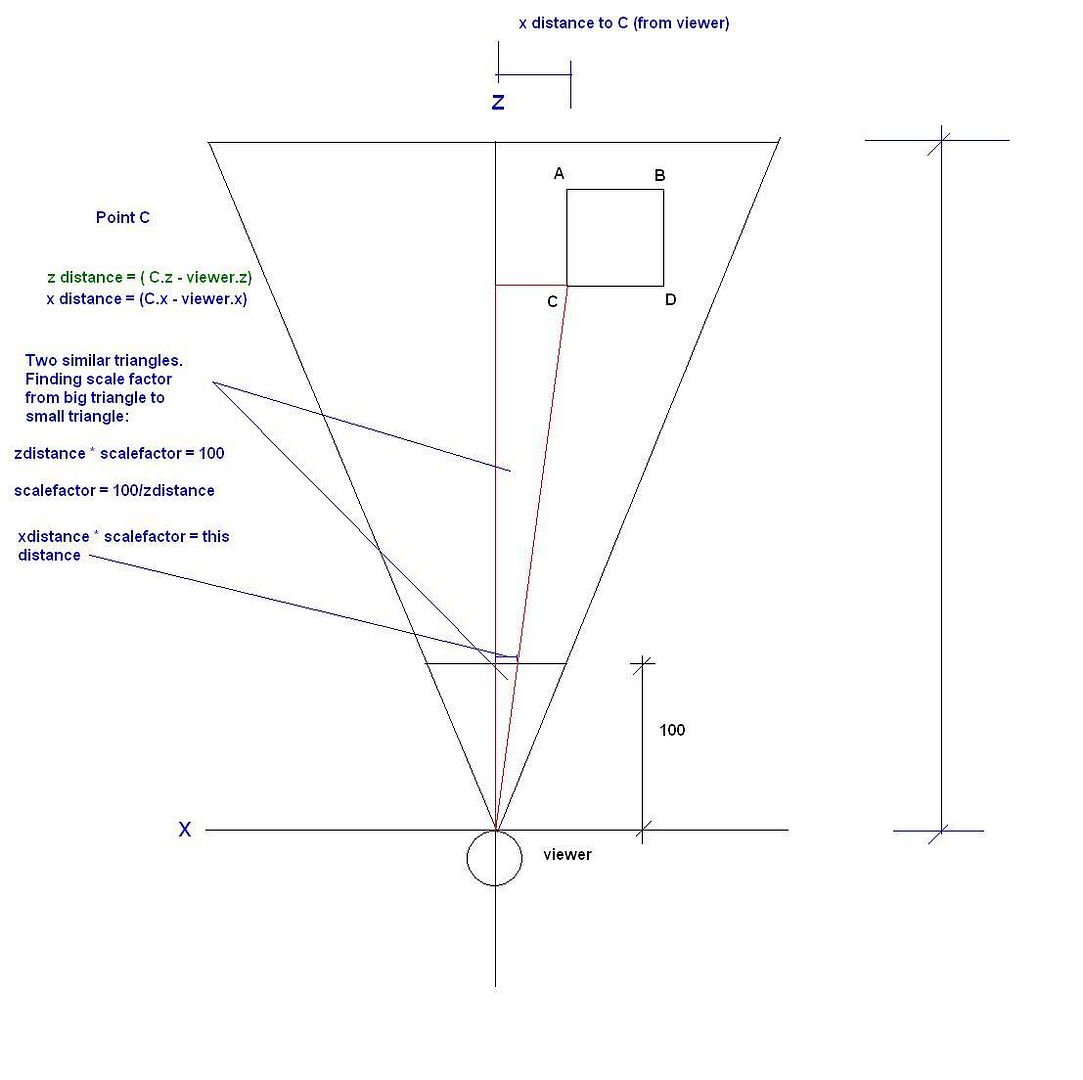
The first pic below illustrates this. If your standing behind a window, looking at a box. And you look at corner C, you are looking through a specific point on the glass. The point where the redline I drew, thats drawn from your eyes to the box, crosses through the window. If you were to draw corner C at that point on the window, and draw all the corners where they intersect the glass, and connect the points with lines. You would see a 3d image of the box exactly as you saw it through the glass.
A computer screen is just like a window to another world so we can do the same to graph 3d points, only it must be done mathematically. First I placed the viewer on an X,Z plane at 0,0. And placed a 2 by 2 box 10 units in front of the viewer. I then placed a small "screen" in front of the viewer. We want to know exactly where every point intersects that screen to graph it.
First we draw a line from the viewer to a point (we'll use point C) Then a line from the viewers location, straight forward, and finally, a line that passes through point C that is paralell to the computer screen or window. We know have two similar triangles. On the big triangle, the horizontal piece is the horizontal distance from the viewer to the point. On the small triangle, this corresponding side is the distance from the center of the computer screen to the point where point C will be placed. Since the triangles are similar all we have to do is scale the parts. We will make the vertical length of the small triangle 100 units. (100 will most likely be bigger number even though its drawn smaller but it still works). We then have to find the scale factor of the big triangle to the small triagnle. First we find the Z distance to the object by subtracting the viewers Z coordinate from the objects Z coordinate. The distance in this case will be 10 since I set the point 10 units out. So now we have corresponding side lengths so we can find the scale factor. 100 * scalefactor = 10. scalefactor = 0.1. We can now use this scale factor to find the horizontal side of the small triangle. We find the x distance from viewer to object by subtracting the viewers x from the objects x. We then multiply by the scale factor to get the length of the small triangle and the location on the computer screen.
This only gave us the new x coordinates. You also need to do the same thing on the Y,Z plane to find the new height as well, but its the same process so I don't think we need to go through it.
The first pic below is an illustration of what we're doing.
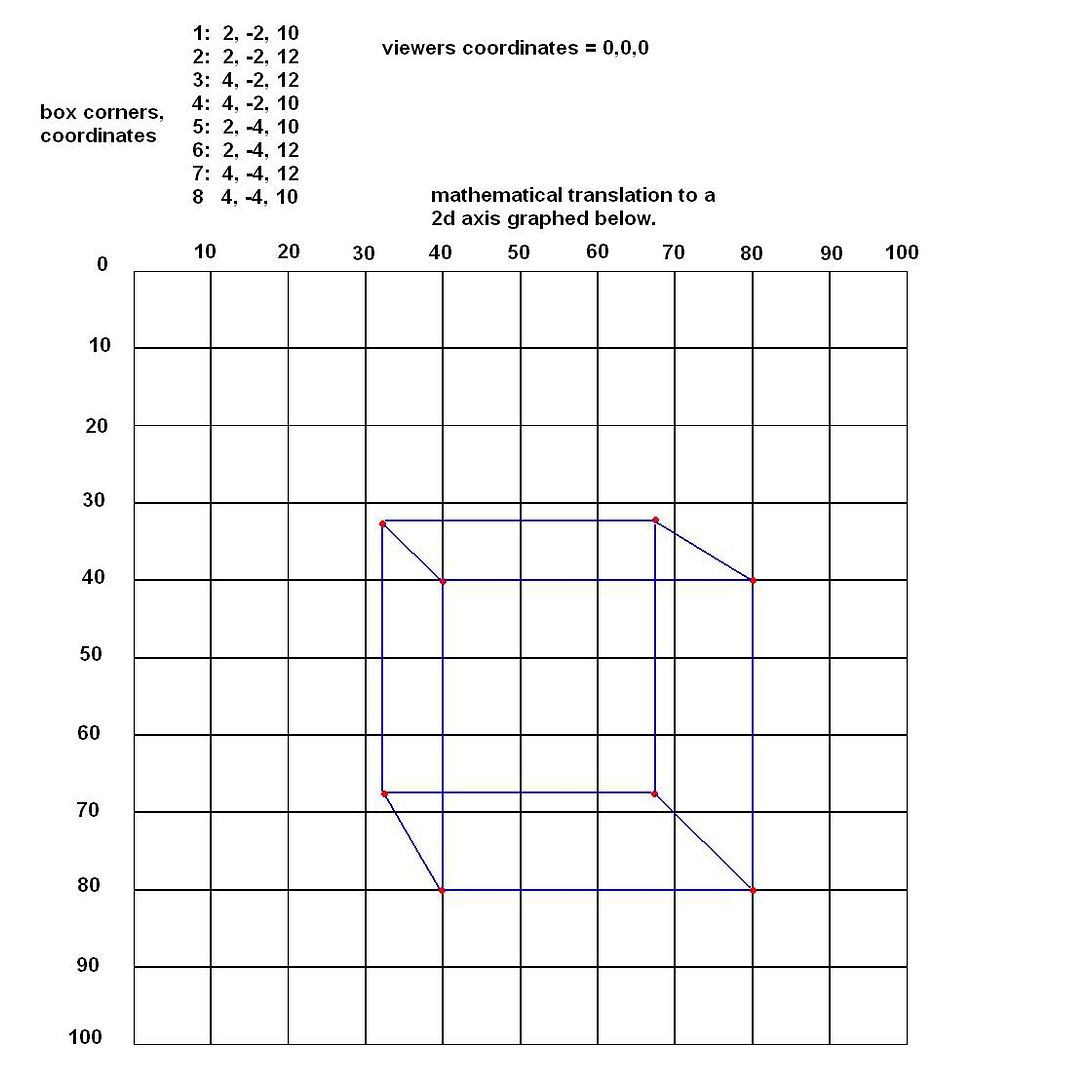
The bottom pic shows using the system with the x,y,z coordinates of a 2 by 2 box 10 units away, translated and graphed using this system. (except I scaled the distances in relation to 200 instead of 100 to make it easier to graph.
results:
First we find the perpendicular distance to the object from the viewer, by finding the z distance between them. We subtract the objects
A logarithm is just a misspelled algorithm.
Offline
#3 2005-10-16 12:40:03
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
This method is fine as far as it goes but has certain obvious drawbacks, it requires the observer be looking paralell to the Z axis. Fortunatly I have developed a function allowing you to rotate your view, which I'll explan shortly.
A logarithm is just a misspelled algorithm.
Offline
#4 2005-10-16 12:59:42
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
To rotate your view by, say, 15 degree's. Yeah you could rotate yourself 15 degree's, but in the case of this program it would be easier to rotate all the objects points around -15 degree's. This would work but theres a problem. The world revolves around you. This is admitably cool but creates problems. An objects location is always changing. I remedied this by using two sets of coordinates. I created a class "point" that holds three coordinatevariables: x, y, and z. And three virtual coordinate variables Vx and Vy. The virtual coordinates are translated and plotted based on the objects real coordinates and the viewers location and angle of view.
First the objects real world coordinates are taken and assigned to temporary variables, these new variables are used in 3d function so the real coordinates are not effected. First the angle to the given point from the viewers location is calculated. (remember my polarangle function? This is what I made it for!) then I use the distance formula ( sqrt (x1 - x2) + (y1 - y2) ) to find the direct distance from the viewer to the point. Now that I have the angle two the object and the distance to the object I know now its polar form. To rotate it, I simply add the negative of the desired roation, and then convert it back to rectangular form. So I remained paralell to the Z axis and rotated the points around me. The virtual points are then assigned the resultant values and the points are plotted. And the real coordinates of the object are completely unchanged.
Again this rotation is done first on the XZ axis (looking left to right) and on the ZY axis (looking up and down) I could also make an XY rotation to flip your view upside down. Easy to do but I don't really need it right now.
Scalling everything in relation to the z distance to the object and rotating the world around you seems pretty restricting and primitive but you can actually use the program without worring about it at all. You can change the viewers coordinates to move around, and rotate your view without a care in the world about how it works. Really the objects are just being translated to the z axis so the perpendicular distance can be easily found.
Heres a quick pic of how the rotation works. (this is down on the XZ axis and ZY axis and the projected)
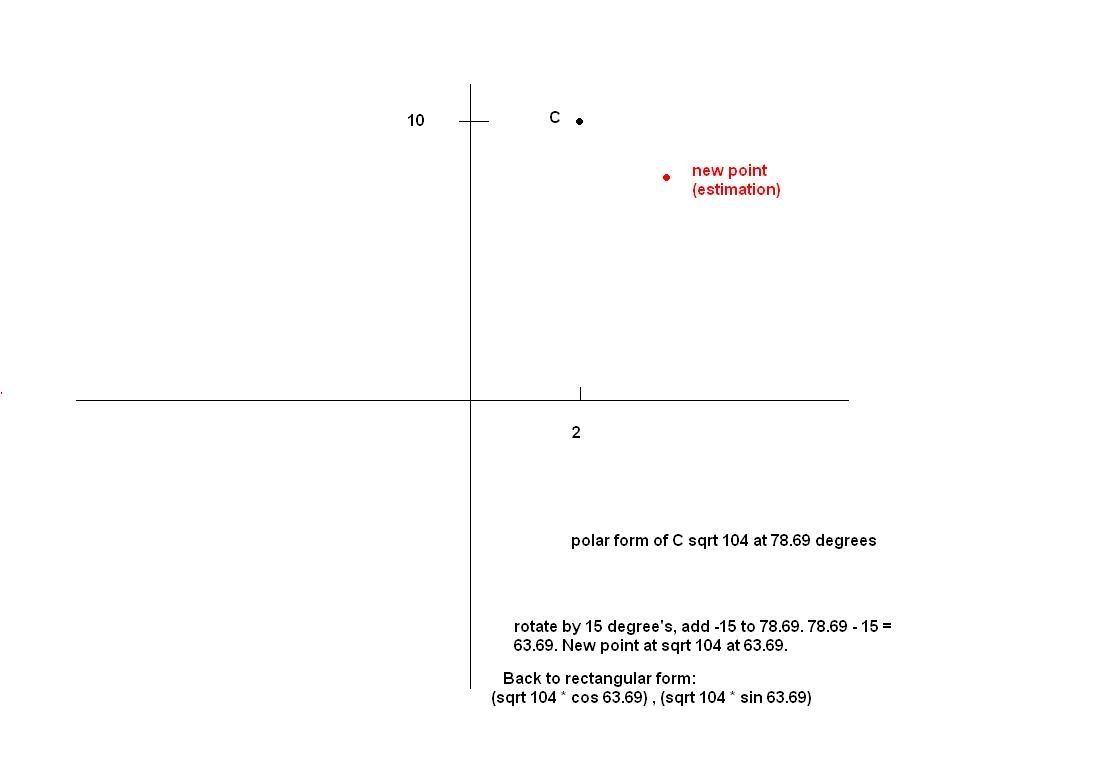
Last edited by mikau (2005-10-16 13:14:09)
A logarithm is just a misspelled algorithm.
Offline
#5 2005-10-16 13:18:16
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
To generalize, the rotation is done using the viewers coordinates the center of rotation. The points are converted to polar form and the desired angle is subtracted from the original polar angle. With this new angle the point is converted back to rectangular form effectively rotating the point around the viewer.
A logarithm is just a misspelled algorithm.
Offline
#6 2005-10-16 13:41:13
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
Some things to consider now. There should be three global variables for the viewers angle of view on the XZ, YZ, and XY axis. My rotation functions only rotate based on a given angle of rotation, you should instead be able to see "I'm looking that way" and the rotation is applied. If you were looking at 90 degree's on the XZ axis, no rotation would be required. At 91, 1 degree of rotation added, at 100, 10 degree's of rotation added. So I suppose 90 degrees must be subtracted everytime. On the YZ axis, if you are looking at zero degree's, no rotation is required so no adjustments are needed.
Now where was I going with that? Ugh..this is confusing.
A logarithm is just a misspelled algorithm.
Offline
#7 2005-10-16 13:43:34
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
Oh yeah. So if your looking set the horizontal viewing angle to 90, no rotation would be made. At 180, 90 degree's of rotation would occur. On the verical axis the angle is ok as it is.
A logarithm is just a misspelled algorithm.
Offline
#8 2005-10-16 13:50:37
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
Then what needs to be considered is objects behind you should not be plotted. After the polarangle check you could compare the angle to the object to your angle of view. If its more then 30 degree's greater or less then the angle at which your looking, then don't display it. This and the "set angle of view" function is something I have yet to make.
Of course this only draws dots. A real 3d engie connects the points with lines and fills in the polygons with color. Also shading and other techniques are applied. Also objects usually have to be opaque and "hide" objects that are behind it so you don't see through everything.
Its complicated and like I said I'm reinventing the wheel, but I enjoy trying to figure things out for myself.
A logarithm is just a misspelled algorithm.
Offline
#9 2005-10-16 14:55:58
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
Ok, I used my program to calculate the Vx and Vy coordinates of that same box, with the angle of view rotated 15 degree's down. I also put the box on the front of a flat surface. Then I used autoCAD to plot the points for me. You can see the box now begins to vanish downward.
Ah... the power of math...
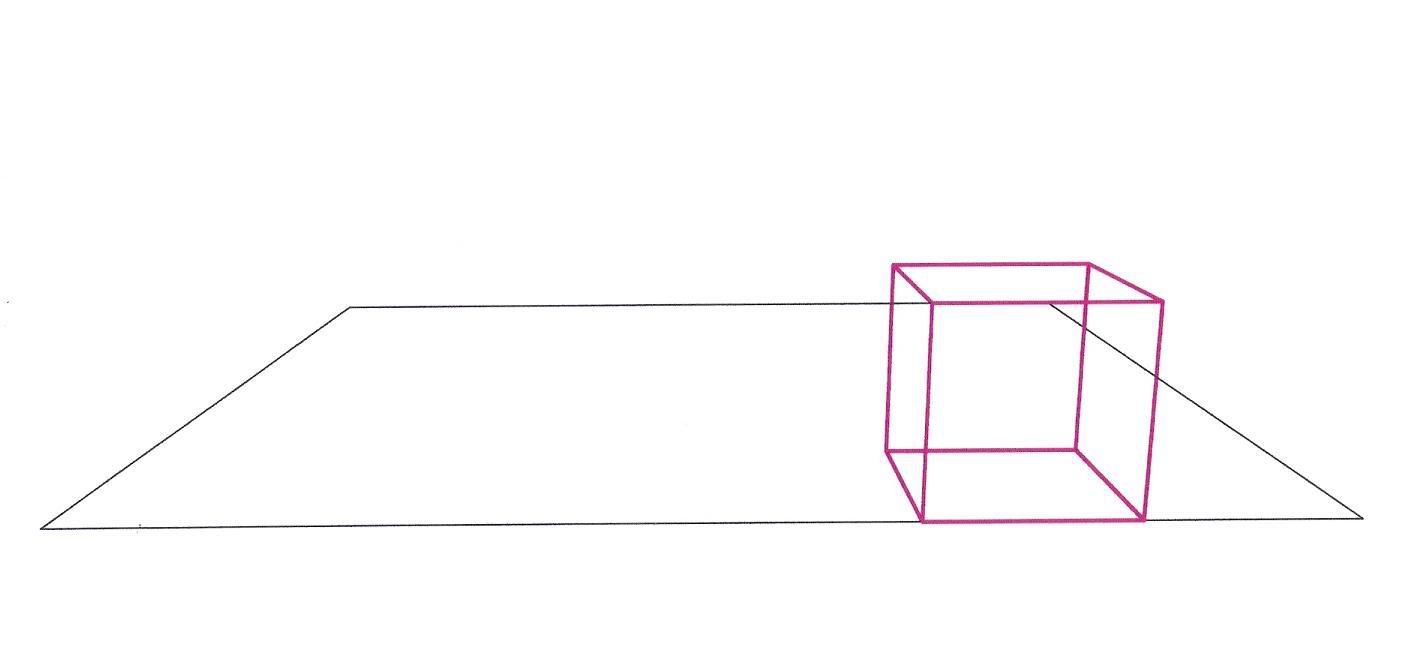
A logarithm is just a misspelled algorithm.
Offline
#10 2005-10-16 18:39:03
- MathsIsFun
- Administrator

- Registered: 2005-01-21
- Posts: 7,713
Re: My 3D engine: reinventing the wheel
Very Impressive!
Looks very realistic - you obviously got the formulas to work for you. People are going to visit here and want to know more.
Now you should be able to draw some other well-known shapes, polyhedra for example.
Also, if you could plot directly to the screen you could have a go at a torus using wireframe (start with just a bunch of small circles going around in a bigger circle). Or perhaps you could rotate the box a little, and then animate it! The power of math indeed!
"The physicists defer only to mathematicians, and the mathematicians defer only to God ..." - Leon M. Lederman
Offline
#11 2005-10-17 01:07:07
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: My 3D engine: reinventing the wheel
Impressive not only for the obvious reason, but also because you managed to do a nontuple post.
Why did the vector cross the road?
It wanted to be normal.
Offline
#12 2005-10-17 05:29:17
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
:-D Thanks guys. But I'm not sure what you mean by a nontuple post.
Yeah what I need is a graphing program to plot the points in realtime. Right now I have to tediously insert the points into the program and plot them manually. I don't know what sort of program I need though.
Yeah animations would be relatively easy if I had a realtime graphing program and access to a timer function so I can set the speed.
Oh and I can rotate the box easy as pi! ;-) All I have to do is speficy the center of rotation in the center of the box, instread of around the viewer, and rotate the box's points using my rotate function. All I need is a realtime grapher and I could have a lot of fun with this.
A logarithm is just a misspelled algorithm.
Offline
#13 2005-10-17 06:02:10
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: My 3D engine: reinventing the wheel
A nontuple post is 9 posts in a row. I don't think anyone has managed that before, despite the fact that we get quite a few spammers!
Why did the vector cross the road?
It wanted to be normal.
Offline
#14 2005-10-17 06:28:00
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
I break my cerebellum to figure out how to write a 3d engine and your impressed that I make nine posts in a row? O_o
A logarithm is just a misspelled algorithm.
Offline
#15 2005-10-17 06:42:20
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
lol. Well anyways I figured I'd post some code now.
Heres another copy of my polarangle function.
float polarangle(float centX, float centY, float objX, float objY)
{float x, y, r;
y = objY - centY; // finding vertical distance from centv, to objvx = objX - centX; //finding horrizontal distance from centh, to objh
if ((x == 0) && (y < 0)) { return 270;} // avoid division by zero
if ((x == 0) && (y > 0)) { return 90; } // avoid division by zero
if ((x == 0) && (y == 0)) { return 0; } // points overlap, no angler = atan(y/x) * 180/3.14159; //calling arctan and converting radians to degree's
if (x < 0) { return (r + 180);}
return r;
}
A logarithm is just a misspelled algorithm.
Offline
#16 2005-10-17 06:45:13
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
Heres the distance formula:
float distance(float obj1X, float obj1Y, float obj2X, float obj2Y)
{
float x =(obj1X - obj2X);
float y = (obj1Y - obj2Y);
std::cout << "distance " << sqrt(x*x + y*y) << "\n";
return sqrt(x*x + y*y);
}
I know I created unecessary variables but it kept screwing up without them. Notice I added some coutstatemts to track program flow and function accuracy.
Last edited by mikau (2005-10-17 06:46:07)
A logarithm is just a misspelled algorithm.
Offline
#17 2005-10-17 06:55:30
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
This function is for converting from polarform back to rectangular form. It takes x,y coordinates of the center, and the x,y coordinates of the object. (the function assumes the angle is in polar form from the center x, y coordinates that you insert). It multiplies the supplied length by the cosine of the angle to find the x distance, this length is then added to the center x coordinate and the x value is assigned this new coordinate. Same goes with y only you use the sine of the angle and add the result to the center y coordinate. Its really hard to explain in words.
void rect(float angle, float length, float centX, float centY, float &x, float &y)
{
y = length * sin(angle * 3.14159/180);
x = length * cos(angle * 3.14159/180);
y += centX;
x += centY;
std::cout << "rect " << x << ", " << y << "\n";
}
x, and y are not used as paremeters to the function, they are only passed into the functions so their values can be reassigned.
Last edited by mikau (2005-10-17 06:56:39)
A logarithm is just a misspelled algorithm.
Offline
#18 2005-10-17 07:02:42
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
Heres the purpose of all those functions. Rotate. This takes the x,y coordinates of a center point and the x,y coordinates of the object, and an angle of rotation. The object is converted to polar form in relation to the center object. Then the angle of rotation is added to its polar angle. This new angle is used when converting back to polar form, rotating the given point by the given degree around the given center point.
void rotate(float angle, float centX, float centY, float &objX, float &objY)
{float dist = distance(centX, centY, objX, objY); // finding distance from specified origin to object
float angleto = polarangle(centX, centY, objX, objY); // finding angle to object from specified origin
std::cout << "orig angle " << angleto << "\n";angleto += angle; // adding rotated angle
std::cout << "new angle " << angleto << "\n";
rect(angleto, dist, centX, centY, objX, objY); // converting back to rectangular form using the new angle
}
A logarithm is just a misspelled algorithm.
Offline
#19 2005-10-17 07:06:41
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
Next we have the class point that has x,y, z and vX, vY member variables. (v for virtual. The points that are used to display the object in 3d)
class point
{
public:
float x;
float y;
float z;
float Vx;
float Vy;
point(float setx, float sety, float setz);
};
I might change the virtual coordinates to integers.
A logarithm is just a misspelled algorithm.
Offline
#20 2005-10-17 07:16:54
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
And heres the 3d projection program. Simply rotates view about the xz axis centered on you, for horizontal rotation, then rotates on the yz axis for vertical rotation. The rotations around you in the negative direction of the angle given. It looks like your turning n degree's to the right, but really everything just moved n degree's to the left. Copies are made of the points coordinates so the rotated and translated points have no effect on the objects real coordinates. :-)
void project(float XZangle, float YZangle, point &thepoint, point viewpoint)
{float tempx = thepoint.x; // creating temporary copies so real coordinates are not effected
float tempy = thepoint.y;
float tempz = thepoint.z;rotate(-XZangle, viewpoint.x, viewpoint.z, tempx, tempz); //XZ rotate
rotate (-YZangle, viewpoint.z, viewpoint.y, tempz, tempy); //YZ rotatefloat zdistance = (tempz - viewpoint.z); //finding directed z distance
float scalefactor = 100/zdistance; // finding scale factor to smaller triangle
thepoint.Vx = ((tempx - viewpoint.x) * scalefactor); // finding directed x distance, scaling down
thepoint.Vy = ((tempy - viewpoint.y) * scalefactor); // finding directed y distance, scaling down
std::cout << "point at " << thepoint.Vx << ", " << thepoint.Vy << "\n";
}
And thats all there is to show so far. I'm sorry a lot of this is sloppy coding. Really a lot of the functions should have certain paremeters declared constant as they will not and should not be changed, I have a lot of polishing to do. I'm just a beginer at C++ so I tend to forget to do things like that.
Thats all there is to it so far.
Last edited by mikau (2005-10-17 07:21:11)
A logarithm is just a misspelled algorithm.
Offline
#21 2005-10-17 10:02:37
- MathsIsFun
- Administrator

- Registered: 2005-01-21
- Posts: 7,713
Re: My 3D engine: reinventing the wheel
I know C++ is a "real language", and Flash only has a "script", but Flash has realtime graphing and you can control time by either frame rate, or spacing your frames.
Example is one I just did on Geometric Translation here: http://www.mathsisfun.com/geometry/translation.html
But Flash costs. Maybe academic price? Or it is available where you study?
Another possibility is Java or Javascript. Anyway, you should know lots of stuff, so you have a full workshop of tools ![]()
"The physicists defer only to mathematicians, and the mathematicians defer only to God ..." - Leon M. Lederman
Offline
#22 2005-10-17 10:32:49
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
Acedemic price? Any sponsering I get at home comes out of my own pocket. lol. I think I'll give myself a scholarship! :-D
Do "visual c++" compilers have graphing programs and stuff? I would assume thats what visual means.
A logarithm is just a misspelled algorithm.
Offline
#23 2005-10-17 16:32:41
- ryos
- Member

- Registered: 2005-08-04
- Posts: 394
Re: My 3D engine: reinventing the wheel
As for "academic price," many companies offer discounts to students, so we can afford (though still just barely) to use their software and hopefully get hooked for life. Creation Engine is a retailer that sells loads of student-priced software.
I think the "visual" is for the way the development works. Though I don't know exactly either, it definitely doesn't have to do with display capabilities.
And, a program to plot and animate coordinates is not hard to write. If you can figure all that 3D junk out, you can figure out plotting.
At least, it's not bad in Java ![]() . If you're working in Win32, it would probably be significantly harder.
. If you're working in Win32, it would probably be significantly harder.
El que pega primero pega dos veces.
Offline
#24 2005-10-17 19:11:10
- MathsIsFun
- Administrator

- Registered: 2005-01-21
- Posts: 7,713
Re: My 3D engine: reinventing the wheel
I use MS Visual Studio (mostly VB.net), and it is great for many things. But for the website I use javascript or Flash.
In fact I bought SwishMax ($100 from http://www.swishzone.com/), which creates Flash, and I like it's environment a bit better. They have academic pricing too, but best of all, they have a 15-day trial which hooked me.
With Flash (or SwishMax) you get a drawing surface where you can put objects and text, and you can also script things. This is how you would draw a series of line on the surface "obj" (I use this to draw the faint lines behind a graph):
obj.lineStyle(0, 0x0000ff, 10);
for (i=0; i<=300; i+=10 ) {
obj.moveTo(i,0); // vertical
obj.lineTo(i,300);
obj.moveTo(0,i); // horizontal
obj.lineTo(300,i);
}"The physicists defer only to mathematicians, and the mathematicians defer only to God ..." - Leon M. Lederman
Offline
#25 2005-11-06 10:56:20
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
Well I found out Game Maker actually has built in trigonometric functions and you can define your own scripts which work pretty much like functions. Game maker's language is pretty primitive as you can't define your own member data, there is only one type of object with preset member data. It has most of what you need but sometimes not being able to define your own can be a real pain. Also you can't pass objects into functions (or scripts) to acess their member data. Each new step has presented new difficulties and I've been forced to copy and recopy large amounts of the same code into each object. Its been a pain in the neck but its working.
Trying to work out some glitches now. The image is completely flawless with zero rotation. You can move around and the dots behave perfectly given their distance and location in relation to the viewer. But rotation seems to be iffy. At times, the rotation appears to be working fine. Other times, the objects get twisted into obviously wrong positions. I set restraints so the object is only visible if its with a 60 degree viewing cone. (if the view is too wide angled barelling is inevitable) Anyway I'm going over my design looking for possible errors, and checking the program for bugs.
Gimme a sec I need to draw up some pictures.
A logarithm is just a misspelled algorithm.
Offline