Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#751 2020-07-04 02:00:02
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
717) James Franck
James Franck was born on August 26, 1882, in Hamburg, Germany. After attending the Wilhelm Gymnasium there, he studied mainly chemistry for a year at the University of Heidelberg, and then studied physics at the University of Berlin, where his principal tutors were Emil Warburg and Paul Drude. He received his Ph.D. at Berlin in 1906 under Warburg, and after a short period as an assistant in Frankfurt-am-Main, he returned to Berlin to become assistant to Heinrich Rubens. In 1911, he obtained the “venia legendi” for physics to lecture at the University of Berlin, and remained there until 1918 (with time out for the war in which he was awarded the Iron Cross, first class) as a member of the physics faculty having achieved the rank of associate professor.
After World War I, he was appointed member and Head of the Physics Division in the Kaiser Wilhelm Institute for Physical Chemistry at Berlin-Dahlem, which was at that time under the chairmanship of Fritz Haber. In 1920, Franck became Professor of Experimental Physics and Director of the Second Institute for Experimental Physics at the University of Göttingen. During the period 1920-1933, when Göttingen became an important center for quantum physics, Franck was closely cooperating with Max Born, who then headed the Institute for Theoretical Physics. It was in Göttingen that Franck revealed himself as a highly gifted tutor, gathering around him and inspiring a circle of students and collaborators (among them: Blackett, Condon, Kopfermann, Kroebel, Maier-Leibnitz, Oppenheimer, and Rabinovich, to mention some of them), who in later years were to be renowned in their own fields.
After the Nazi regime assumed power in Germany, Franck and his family moved to Baltimore, U.S.A., where he had been invited to lecture as Speyer Professor at Johns Hopkins University. He then went to Copenhagen, Denmark, as a guest professor for a year. In 1935, he returned to the United States as Professor of Physics at Johns Hopkins University, leaving there in 1938 to accept a professorship in physical chemistry at the University of Chicago. During World War II Franck served as Director of the Chemistry Division of The Metallurgical Laboratory at the University of Chicago, which was the center of the Manhattan District’s Project.
In 1947, at the age of 65, Franck was named professor emeritus at the University of Chicago, but he continued to work at the University as Head of the Photosynthesis Research Group until 1956.
While in Berlin Professor Franck’s main field of investigation was the kinetics of electrons, atoms, and molecules. His initial researches dealt with the conduction of electricity through gases (the mobility of ions in gases). Later, together with Hertz, he investigated the behaviour of free electrons in various gases – in particular the inelastic impacts of electrons upon atomswork which ultimately led to the experimental proof of some of the basic concepts of Bohr’s atomic theory, and for which they were awarded the Nobel Prize, for 1925. Franck’s other investigations, many of which were carried out with collaborators and students, were also dedicated to problems of atomic physics – those on the exchange of energy of excited atoms (impacts of the second type, photochemical researches), and optical problems connected with elementary processes during chemical reactions.
During his period at Göttingen most of his studies were dedicated to the fluorescence of gases and vapours. In 1925, he proposed a mechanism to explain his observations of the photochemical dissociation of iodine molecules. Electronic transitions from a normal to a higher vibrational state occur so rapidly, he suggested, that the position and momenta of the nuclei undergo no appreciable change in the process. This proposed mechanism was later expanded by E. U. Condon to a theory permitting the prediction of most favoured vibrational transitions in a band system, and the concept has since been known as the Franck-Condon principle.
Mention should be made of Professor Franck’s courage in following what was morally right. He was one of the first who openly demonstrated against the issue of racial laws in Germany, and he resigned from the University of Göttingen in 1933 as a personal protest against the Nazi regime under Adolf Hitler. Later, in his second homeland, his moral courage was again evident when in 1945 (two months before Hiroshima) he joined with a group of atomic scientists in preparing the so-called “Franck Report” to the War Department, urging an open demonstration of the atomic bomb in some uninhabited locality as an alternative to the military decision to use the weapon without warning in the war against Japan. This report, although failing to attain its main objective, still stands as a monument to the rejection by scientists of the use of science in works of destruction.
In addition to the Nobel Prize, Professor Franck received the 1951 Max Planck Medal of the German Physical Society, and he was honoured, in 1953, by the university town of Göttingen, which named him an honorary citizen. In 1955, he received the Rumford Medal of the American Academy of Arts and Sciences for his work on photosynthesis, a subject with which he had become increasingly preoccupied during his years in the United States. In 1964, Professor Franck was elected as a Foreign Member of the Royal Society, London, for his contribution to the understanding of exchanges of energy in electron collisions, to the interpretation of molecular spectra, and to problems of photosynthesis.
Franck was first married (1911) to Ingrid Josefson, of Göteborg, Sweden, and had two daughters, Dagmar and Lisa. Some years after the death of his first wife, he was married (1946) to Hertha Sponer, Professor of Physics at Duke University in Durham, North Carolina (U.S.A.).
Professor Franck died in Germany on May 21, 1964, while visiting in Göttingen.

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#752 2020-07-06 01:08:58
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
718) Harlow Shapley
Harlow Shapley, (born November 2, 1885, Nashville, Missouri, U.S.—died October 20, 1972, Boulder, Colorado), American astronomer who deduced that the Sun lies near the central plane of the Milky Way Galaxy and was not at the centre but some 30,000 light-years away.
In 1911 Shapley, working with results given by Henry Norris Russell, began finding the dimensions of stars in a number of binary systems from measurements of their light variation when they eclipse one another. These methods remained the standard procedure for more than 30 years. Shapley also showed that Cepheid variables cannot be star pairs that eclipse each other. He was the first to propose that they are pulsating stars.
Shapley joined the staff of the Mount Wilson Observatory, Pasadena, California, in 1914. Employing the 1.5-metre (60-inch) reflecting telescope at Mount Wilson, he made a study of the distribution of the globular clusters in the Milky Way Galaxy; these clusters are immense, densely packed groups of stars, some containing as many as 1,000,000 members. He found that of the 100 clusters known at the time, one-third lay within the boundary of the constellation Sagittarius. Using the newly developed concept that RR Lyrae variable stars accurately reveal their distance by their period of variation and apparent brightness, he found that the clusters were distributed roughly in a sphere whose centre lay in Sagittarius. Since the clusters assumed a spherical arrangement, it was logical to conclude that they would cluster around the centre of the Galaxy; from this conclusion and his other distance data Shapley deduced that the Sun lies at a distance of about 50,000 light-years from the centre of the Galaxy; the number was later corrected to 30,000 light-years. Before Shapley, the Sun was believed to lie near the centre of the Galaxy. His work, which led to the first realistic estimate for the actual size of the Galaxy, thus was a milestone in galactic astronomy.
At this time, the nature of the spiral nebulae, such as that of Andromeda, was a subject of much debate. On April 26, 1920, Shapley and American astronomer Heber Curtis debated “the scale of the Universe” at a meeting of the National Academy of Sciences in Washington, D.C. Their “Great Debate,” as it came to be called, had no clear winner. Curtis did not believe in Shapley’s size for the Milky Way, but his belief that the spiral nebulae were other galaxies (“island universes”) proved correct. Shapley had correctly appreciated the Galaxy’s great size but posited a universe consisting entirely of the Milky Way with the spiral nebulae as objects like the globular clusters.
In addition to his studies of the Galaxy, Shapley studied the neighbouring galaxies, especially the Magellanic Clouds, and found that galaxies tend to occur in clusters, which he called metagalaxies. In 1953 he proposed the “liquid water belt” theory, which stated that a planet had to be a certain distance from its star to develop an atmosphere and have liquid water, and therefore life. This concept is now called the habitable zone. Shapley became professor of astronomy at Harvard University, later director of Harvard College Observatory (1921–52), and was made director emeritus and Paine Professor of Astronomy at Harvard in 1952. His works include ‘Star Clusters’ (1930), ‘Flights from Chaos, (1930), ‘Galaxies’ (1943), ‘The Inner Metagalaxy’ (1957), and ‘Of Stars and Men: The Human Response to an Expanding Universe’ (1958; film 1962). He was the father of Nobel Prize-winning economist Lloyd Shapley.

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#753 2020-07-08 00:21:36
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
719) Karl Jansky
Karl Jansky, in full Karl Guthe Jansky, (born October 22, 1905, Norman, Oklahoma, U.S.—died February 14, 1950, Red Bank, New Jersey), American engineer whose discovery of radio waves from an extraterrestrial source inaugurated the development of radio astronomy, a new science that from the mid-20th century greatly extended the range of astronomical observations.
In 1928 Jansky joined the Bell Telephone Laboratories in New Jersey, where his assignment was to track down and identify the various forms of interference that were plaguing telephone communications. He built a linear, directional antenna by which he was able to identify all the sources of interference except one. After months of study he discovered in 1931 that the source of the unidentified radio interference came from the stars. By the following spring he concluded that the source lay in the direction of the constellation Sagittarius, which Harlow Shapley and Jan Oort had established as the direction of the centre of the Milky Way Galaxy.
Jansky published his findings in late 1932 but did not pursue the further development of radio astronomy, a task performed by the American engineer and amateur astronomer Grote Reber. In honour of Jansky’s epoch-making discovery, the unit of radio-wave emission strength was named the jansky.

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#754 2020-07-10 00:49:01
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
720) Karl Jatho
Karl Jatho (3 February 1873 – 8 December 1933) was a German pioneer and inventor, performer and public servant of the city of Hanover.
From August through November 1903, Jatho made progressively longer hops (flights) in a pusher triplane, then biplane, at Vahrenwalder Heide outside of Hanover. His first flight, was only 18 meters at about 1 meter altitude, and was not controlled. Jatho eventually gave up, noting "In spite of many efforts, (I) cannot make longer or higher flights. Motor weak.". With a later machine, Jatho would make successful flights in 1909 – 60 meters at about at 3–4 meters altitude. He also founded a flying school and an aircraft factory, but did not have much success.

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#755 2020-07-12 00:55:35
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
721) Herman Hollerith
Herman Hollerith, (born February 29, 1860, Buffalo, New York, U.S.—died November 17, 1929, Washington, D.C.), American inventor of a tabulating machine that was an important precursor of the electronic computer.
Immediately after graduation from the Columbia University School of Mines in 1879, Hollerith became an assistant to his teacher William P. Trowbridge in the U.S. census of 1880. During the next decade he taught briefly at the Massachusetts Institute of Technology, Cambridge; experimented on air brakes; and worked for the Patent Office in Washington, D.C. During all this time he was occupied with the problem of automating the tabulation work of the census. By the time of the census of 1890, he had invented machines to record statistics by electrically reading and sorting punched cards that had been numerically encoded by perforation position. The invention was a success in the United States but drew much more attention in Europe, where it was widely adopted for a number of statistical purposes. In 1896 Hollerith organized the Tabulating Machine Company, incorporated in New York, to manufacture the machines; through subsequent mergers it grew into the International Business Machines Corporation (IBM).
Herman Hollerith (February 29, 1860 – November 17, 1929) was an American statistician and inventor. He developed a mechanical tabulator based on punched cards. This tabulated (put into tables) the data from millions of people. He was the founder of the Tabulating Machine Company that later became IBM.
Hollerith is as a father of modern machine data processing. The start of automatic data processing systems came with his invention. Programs and data were put in to computer by punched cards in the 1950s and 60s.
Hollerith began working for the United States Census Bureau in the year he filed his first patent application. Titled "Art of Compiling Statistics", it was filed on September 23, 1884; U.S. Patent 395,782 was granted on January 8, 1889.
Hollerith built machines under contract for the Census Office, which used them to tabulate the 1890 United States Census in only one year. The previous 1880 United States Census had taken eight years.
Hollerith started his ‘Tabulating Machine Company’ in 1896. Major census bureaus around the world leased his equipment and purchased his cards, as did major insurance companies. Hollerith's machines were used for censuses in England, Italy, Germany, Russia, Austria, Canada, France, Norway, Puerto Rico, Cuba, and the Philippines, and again in the 1900 United States Census . To make his system work, he invented the first automatic card-feed mechanism and the first keypunch (that is, a punch operated by a keyboard); a skilled operator could punch 200–300 cards per hour. He also invented a tabulator.
.
It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#756 2020-07-14 00:20:39
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
722) Nick Holonyak, Jr.
Nick Holonyak, Jr., (born November 3, 1928, Zeigler, Illinois, U.S.), American engineer who was known for his pioneering work with light-emitting diodes (LEDs), notably creating the first visible LED.
Holonyak was the son of immigrants from what is now Ukraine. He studied electrical engineering at the University of Illinois at Urbana-Champaign, where he received B.S. (1950), M.S. (1951), and Ph.D. (1954) degrees. He was the first graduate student of two-time Nobel Prize recipient John Bardeen, a joint inventor of the transistor.
After Holonyak spent a year (1954–55) working at Bell Telephone Laboratories and two years (1955–57) in the military, he joined the General Electric (GE) electronics laboratory in Syracuse, New York. Several GE teams were working in the field of optoelectronics, the conversion of electric current into light. GE colleague Robert N. Hall had developed a laser using a semiconductor diode (a semiconductor device with positive and negative electrodes that can serve as a rectifier—that is, a converter of alternating current to direct current). Hall’s laser emitted only infrared radiation, which lies beyond the range of human vision. Holonyak decided to make a diode device that would emit visible light. By using the semiconductor material GaAsP and the technique of stimulated emission, in 1962 Holonyak succeeded in operating the first practical visible LED device. Holonyak’s device emitted red light. After LEDs that produce green and blue light were developed (in the 1970s and ’90s, respectively), LEDs that emit white light became possible, revolutionizing the lighting industry. Among his other work for GE, in 1959 Holonyak was the first to make silicon tunnel diodes and the first to observe phonon-assisted tunneling.
In 1963 Holonyak left GE to take up a professorship at the University of Illinois, where in 1993 he was named to the John Bardeen Endowed Chair in Electrical and Computer Engineering and Physics. At Illinois, Holonyak pioneered the use of a number of alloys in diodes, and in 1977 he and a student made the first quantum-well laser diode. Holonyak retired as professor emeritus in 2013.
Holonyak was a member of the National Academy of Engineering and the National Academy of Sciences, a fellow of the American Academy of Arts and Sciences, a fellow of the American Physical Society, a foreign member of the Russian Academy of Sciences, and a life member of the Institute of Electrical and Electronics Engineers (IEEE). His numerous awards included the Edison Medal of the IEEE (1989), the National Medal of Science (1990), the Japan Prize (1995), the IEEE Third Millennium Medal (2000), the IEEE Medal of Honor (2003), and the Lemelson-MIT Prize (2004). In 2015 Holonyak was one of five engineers awarded the Charles Stark Draper Prize, administered by the National Academy of Engineering; two of the other honorees, George Craford and Russell Dupuis, were former graduate students of Holonyak.

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#757 2020-07-14 20:58:41
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
723) John Horton Conway
John Horton Conway, a legendary mathematician who stood out for his love of games and for bringing mathematics to the masses, died on Saturday, April 11, in New Brunswick, New Jersey, from complications related to COVID-19. He was 82.
(26 December 1937 – 11 April 2020)
Known for his unbounded curiosity and enthusiasm for subjects far beyond mathematics, Conway was a beloved figure in the hallways of Princeton’s mathematics building and at the Small World coffee shop on Nassau Street, where he engaged with students, faculty and mathematical hobbyists with equal interest.
Conway, who joined the faculty in 1987, was the John von Neumann Professor in Applied and Computational Mathematics and a professor of mathematics until 2013 when he transferred to emeritus status.
“John Conway was an amazing mathematician, game wizard, polymath and storyteller who left an indelible mark on everyone he encountered — colleagues, students and beyond — inspiring the popular imagination just as he unraveled some of the deepest mathematical mysteries,” said Igor Rodnianski, professor of mathematics and chair of the Department of Mathematics. “His childlike curiosity was perfectly complemented by his scientific originality and the depth of his thinking. It is a great loss for us and for the entire mathematical world.”
Over his long career, Conway made significant contributions to mathematics in the fields of group theory, number theory, algebra, geometric topology, theoretical physics, combinatorial game theory and geometry.
“He was like a butterfly going from one thing to another, always with magical qualities to the results,” said Simon Kochen, professor of mathematics, emeritus, a former chair of the department, and a close collaborator and friend.
Kochen went on to say that Conway was a “magical genius,” defined as a person who is not merely smarter than most people but whose mind works in highly advanced and unfathomable ways. The term was coined by the late mathematician Mark Kac to describe the physicist Richard Feynman.
One of Conway’s most well-known accomplishments was the Game of Life, which he conceived in the 1970s to describe how life can evolve from an initial state. The concept builds on ideas that trace back to John von Neumann, a pioneer of early computing, in the 1940s. Conway’s game involves a two-dimensional grid in which each square cell interacts with its neighbors according to a set of rules. Over time, these simple interactions give rise to complexity.
The game was introduced in an October 1970 issue of Scientific American’s mathematical games column, whose creator, the late Martin Gardner, was friends with Conway. Conway continued his interest in “recreational mathematics” by inventing numerous games and puzzles. At Princeton, he often carried in his pockets props such as ropes, pennies, cards, dice, models and sometimes a Slinky to intrigue and entertain students and others.
Manjul Bhargava, who was advised by Conway during his first year as a graduate student at Princeton and who is now Princeton’s Brandon Fradd, Class of 1983, Professor of Mathematics, said that Conway’s love for games and magic tricks as a way to teach mathematical concepts inspired Bhargava’s own approach.
“I learned very quickly that playing games and working on mathematics were closely intertwined activities for him, if not actually the same activity,” Bhargava said. “His attitude resonated with and affirmed my own thoughts about math as play, though he took this attitude far beyond what I ever expected from a Princeton math professor, and I loved it.”
Conway’s genius led to many discoveries and accomplishments far deeper and more fundamental than the Game of Life, according to Peter Doyle, a longtime friend and collaborator, and a professor of mathematics at Dartmouth College. “People invariably describe Conway as the inventor of the Game of Life,” Doyle said. “That’s like describing Bob Dylan as the author of ‘Blowin’ in the Wind.‴
The achievement for which Conway himself was most proud, according to Kochen, was his invention of a new system of numbers, the surreal numbers. This continuum of numbers includes not only real numbers such as integers, fractions and irrational numbers such as pi, but also the infinitesimal and infinite numbers.
Later, with Kochen, Conway developed and proved the Free Will Theorem in 2004 to explain principles of quantum mechanics, the branch of physics that dictates the behaviors of atoms and other elementary particles. It states that if an experimenter can freely choose what to measure in a particular experiment, then elementary particles can also freely choose their spins in order to make the measurements consistent with physical law.
The Free Will Theorem gained attention for its implication that if humans have free will, then elementary particles — like atoms and electrons — also possess free will.
Conway’s numerous honors include the London Mathematical Society’s Berwick Prize and Pólya Prize, Northwestern University’s Nemmers Prize in Mathematics, and the American Mathematical Society’s Leroy P. Steele Prize for Mathematical Exposition. Conway is a fellow of the Royal Society of London and the American Academy of Arts and Sciences.
Conway was born in Liverpool, England, on December 26, 1937. He received his B.A. from Cambridge University in 1959 and his Ph.D. from the same institution in 1964. He was a faculty member at Cambridge until he came to Princeton.
David Gabai, the Hughes-Rogers Professor of Mathematics and former chair of the department, remarked, “John Conway was a beloved faculty member of the department, always very friendly and ready to chat with anyone. People would come from far away to talk to him.”
Conway’s regular office was filled to overflowing with books and colorful toy models, built from paper and wood to illustrate mathematical concepts, so he typically could be found sitting in one of the small nooks across from the common room in Fine Hall, Gabai added. There, Conway would talk to students and colleagues, or be engrossed in writing at the adjacent blackboard or with a pen and pad of paper.
Peter Sarnak, Princeton’s Eugene Higgins Professor of Mathematics, recalled those days.
“An extrovert by nature, John liked to be at the center of mathematical discussions and he enjoyed thinking and inventing on the spot,” Sarnak said. “To this end he gave up his regular office in the Princeton mathematics department and moved into the big common room where he could always be found holding court on the latest (often his!) mathematical development or invention. On days of little mathematical news he would be challenging others to mathematical games or puzzles and now that I think of it, I can’t recall any instance where he did not win.
“The mathematical world has lost a very special person but we are much richer for all that he gave us.”
Conway made numerous advances in many areas of mathematics. In group theory, he worked on the classification of finite simple groups and discovered the Conway groups, and was the primary author of the ATLAS of Finite Groups in 1986. With Simon Norton at Cambridge in 1979, he conceived of the complex of conjectures named “Monstrous Moonshine.” He also investigated lattices in higher dimensions, and with Neil Sloane at Bell Labs authored Sphere Packings, Lattices and Groups in 1988.
In number theory, Conway proved as a graduate student the conjecture by Cambridge’s Edward Waring that every integer could be written as the sum of 37 numbers, each raised to the fifth power. In 1993 at Princeton, he proved with former student William Schneeberger, that if an integral positive definite quadratic form with integer matrix represents all positive integers up to 15, then it represents all positive integers.
Working with quaternions, he invented the system of icosians in algebra. He was the author of several books and monographs, including “On Quaternions and Octonions” in 2003, with former student Derek Smith, now a professor at Lafayette College, “The Sensual (Quadratic) Form” in 1997 with former student Francis Fung, and “Regular Algebra and Finite Machines” in 1971.
In geometric topology, Conway made contributions to knot theory and a variant now called the Alexander-Conway polynomial. He further developed tangle theory and invented a system of notation for tabulating knots, now known as Conway notation, while extending the knot tables to 11 crossings.
“He was really without exaggeration a genius, absolutely” said Joseph Kohn, professor of mathematics, emeritus, and a former chair of the department. “He knew so many things and he was interested in all aspects of mathematics and science. He was an enthusiastic teacher; he liked to share his knowledge and discuss things. He was very playful, and always ready to have a game, many of which he invented himself.”
Kohn related a time when Conway had committed to giving a large public lecture and on the way to the lecture, asked his companions what topic he should cover. Upon deciding on the topic in the car, Conway successfully gave the lecture without any additional preparation.
Conway combined playfulness with a mastery of esoteric information, several who knew him commented.
“Once he shook my hand and informed me that I was four handshakes away from Napoleon, the chain being me, John Conway, Bertrand Russell, Lord John Russell and Napoleon,” Gabai said.
Conway’s wife, Diana, first met Conway in 1996 in a coffee shop on Witherspoon Street in Princeton where they were both regular morning customers. The two discovered that they shared a love of games and became friends. At the time, Diana worked at the University bookstore and though not a mathematician, enjoyed math and later became an accountant. They married in 2001.
“John was the most fascinating human being I’ve ever met,” said Diana Conway. “He was not only interested in math, he was interested in everything.”
Diana Conway described John Conway’s willingness to talk to anyone interested in mathematics, whether another university professor or a hobbyist with an interesting theory or discovery.
“There were always strange characters showing up at our house, joining us for dinner, or sitting with John out in the back garden,” said Diana Conway. “He would get buckets and buckets of fan mail.”
Conway’s passion for teaching extended not just to University undergraduates but also to high school and middle school students at regional math camps held during summers at universities around the country. Diana and their young son Gareth would accompany him.
Conway is survived by Diana Conway and son Gareth. He is also survived by sons Alex and Oliver from his second marriage to wife Larissa; and daughters Susie, Rosie, Ellie and Annie from his first marriage to wife Eileen Howe. He is also survived by three grandchildren and six great-grandchildren.

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#758 2020-07-16 00:43:16
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
724) Donald Ervin Knuth
Born : 10 January 1938 : Milwaukee, Wisconsin, USA
Summary :
Donald Knuth is an American mathematician most famous for inventing the LaTeX typesetting language.
Biography
Donald Knuth's parents were Ervin Henry Knuth and Louise Marie Bohning. Donald's father Ervin was a school teacher who taught in a Lutheran school. He played a very important role in determining Donald's interests, and it was through his father that that Donald gained his love for education, music, and mathematics. Ervin played the church organ at the Sunday church services and Donald soon became a passionate lover of the organ.
Donald attended Lutheran schools and from the special emphasis that was placed on English grammar in these schools came Knuth's love of investigating sentence structure. His fascination with this in his first couple of years of secondary school would lead naturally towards writing computer code when he eventually encountered computers, but this did not happen until after his school education was complete. During these first years at secondary school there were other signs of where Knuth's interests would eventually lead. One episode, repeated in most biographies of Knuth but still worth repeating in this one, concerns "Ziegler's Giant Bar."
He entered a competition set up by the confectionary manufacturer Ziegler. The aim was to see how many words could be made with the letters of "Ziegler's Giant Bar" and for the schoolboy Knuth this was exactly the sort of challenge that he loved. He spent two weeks during which he pretended to be ill and, using a dictionary, he came up with 4500 words. The judges for the competition had only found 2500 and Knuth was an easy winner. He commented afterwards that had he thought to use the apostrophe he could have found many more! His school benefited by receiving a television set as a prize.
At high school Knuth's interests were more directed towards music than they were to mathematics. His musical interests involved both playing and composing music and he decided at that stage that he would study music after graduating from high school. Knuth played the saxophone, and later the tuba, in his school band. Although he spent much time with his musical interests, Knuth most certainly did not neglect his other school subjects. He graduated from High School in 1956 with the highest grade point average that anyone had ever achieved at his school.
At school he had begun to show an interest in mathematics and he amused himself by trying to visualise surfaces in several dimensions by plotting the graphs obtained by keeping all but one of the variables fixed. This is an excellent way to understand mathematical functions and today with the aid of computers this, and more sophisticated techniques, can quickly give students a deep understanding. However Knuth had to plot his graphs by doing hand calculations for every value which he plotted, showing the same sort of dedication to putting hours of work into problems that he had shown with the "Ziegler's Giant Bar" competition. One might have thought that his teachers would have believed that he could succeed at college in almost any subject he chose given his outstanding school performance, but this was not really so. The problem was that Knuth did not believe in himself at this stage in his life and so his teachers doubted whether he had the personality, in particular the confidence, to succeed.
It shows how undecided Knuth was about the direction his studies might take that when offered a scholarship to Case Institute of Technology in Cleveland, Ohio, to study physics he accepted despite his previous intentions to study music. He entered the physics course at the Case Institute in September 1956. There were really two reasons why, from his second year on, Knuth started to move towards mathematics and away from physics. One day when Knuth was meant to be performing with the College band he missed the bus taking the band to the performance so, finding himself with free time, he tried to solve a challenge problem that one of his mathematics professors had set. Solving it earned Knuth an automatic "A" in that class and also the right sort of boost he needed to think that perhaps mathematics rather than physics was for him. Secondly he found that physics practicals did not suit him, so in the end the move towards mathematics became a natural one to make.
In fact Knuth already had his first encounter with computers in his first year at Case before he made the move towards mathematics. He had to use the IBM 650 and consulted the manual to find out how to write programs :-
... the manual we got from IBM would show examples of programs and I knew I could do ... better than that. So I thought I might have some talent.
Knuth used his growing expertise at writing computer programs to produce one in 1958 to analyse the performance of the College basketball team. It led to some publicity and IBM used a photograph of Knuth in their advertising. One might have expected that events would begin to help him overcome his inferiority complex but he still felt that he was not up to standard. This had the effect of making him put in large amounts of extra work at his academic studies. The result was that when he graduated with his B.S. in June 1960 he was awarded a distinction and, in a quite unique move, the College awarded him a Master's Degree at the same time, such was the brilliance of his performance. Knuth was awarded two Fellowships, a Woodrow Wilson Fellowship and a National Foundation Fellowship in the year of his graduation.
It is a real achievement to publish a mathematics paper while still a doctoral student, but Knuth managed to publish two papers in the year he completed his undergraduate degree. These were An imaginary number system and On methods of constructing sets of mutually orthogonal Latin squares using a computer I the latter paper being written jointly with R C Bose and I M Chakravarti. In the first Knuth describes an imaginary number system using the imaginary number 2i as its base, giving methods for the addition, subtraction and multiplication of the numbers. In the second paper Knuth and his co-authors give two sets of five mutually orthogonal Latin squares of order 12.
In the autumn of 1960 Knuth entered the California Institute of Technology and, in June 1963, he was awarded a Ph.D. in mathematics for his thesis Finite semifields and projective planes. In fact in addition to the work for his doctorate in mathematics, Knuth had from 1960 begun to put his very considerable computing expertise to uses other than writing papers becoming a software development consultant to the Burroughs Corporation in Pasadena, California. Knowledge of his computing expertise was so well established by 1962 that, although he was still a doctoral student at the time, Addison-Wesley approached him and asked him to write a text on compilers. He began that project in the summer of 1962.
His publications from this time show that he was applying computing to combinatorial mathematical problems which were not connected to the work he was undertaking for his thesis. For example he computed Euler's constant to 1271 decimal places and published the result in 1962. In the same year he published work on the evaluation of polynomials by computer. Despite Knuth's remarkable mathematical productivity he did find time for other things. During his years as a graduate student Knuth married Nancy Jill Carter on 24 June 1961. Their two children John Martin Knuth and Jennifer Sierra Knuth were born in 1965 and 1966 respectively.
We noted above that the title of Knuth's Ph.D. thesis was Finite semifields and projective planes. A semifield is an algebraic structure satisfying all the usual axioms for a division ring except associativity of multiplication. The thesis contains a wealth of information on finite semifields and their connections to certain types of projective planes. After completion of his doctorate in 1963 Knuth became an Assistant Professor of Mathematics at the California Institute of Technology, being promoted to Associate Professor in 1966. From 1964 to 1967 he worked as an Editor of Programming Languages for the Association for Computing Machinery. He continued to apply computing to algebraic and combinatorial mathematics problems. For example in 1964 he published tables of data for finite fields which enabled rapid computer calculations to be carried out. His great love of music, which he had almost devoted his life to, continued and in 1965 he joined the American Guild of Organists. He would continue to play music, compose music and has even designed of his own pipe organ.
By 1966 his book on compilers had grown to 3000 handwritten pages and Addison-Wesley realised that here was a much more major work than they had originally envisaged. Discussions led to a decision that Knuth should produce a seven volume work covering much more than compilers. The work became The Art of Computer Programming and publication began in 1968 when Volume 1: Fundamental Algorithms appeared. Volume 2: Seminumerical algorithms came out in the following year, and Volume 3: Sorting and searching in 1973. In the Preface Knuth writes that these are:-
... books that have been designed to train the reader in the various skills which go into a programmer's craft... [They are] not meant to serve as an introduction to computer programming; the reader is supposed to have some previous experience. [I aim to provide] (a) reference books which summarize the knowledge which has been acquired in several important fields, and (b) textbooks for self-study or for college courses in the computer and information sciences.
Knuth's aim was to:-
... organize and summarize what is known about the fast subject of computer methods and to give it firm mathematical and historical foundations.
... show that the connection between computers and mathematics is far deeper and more intimate than these traditional relationships would imply.
M Muller, reviewing these wonderful books, writes that:-
Knuth has already made a timely and great contribution. He has managed to provide organization of ideas where little existed before; he has provided many ideas which in essence are new and helpful in obtaining a basis of abstraction, integration, or unification of efforts of earlier workers in the various fields covered.
In 1968 Knuth was appointed as Professor of Computer Science at Stanford University. At the same time as he left the California Institute of Technology he also resigned his consultancy position with the Burroughs Corporation. Knuth remained at Stanford University for the remainder of his career. He was appointed Fletcher Jones Professor of Computer Science in 1977 and in 1990 he was named Professor of The Art of Computer Programming. In 1993 he became Professor Emeritus at Stanford University and continued to live on the University Campus.
Knuth has made many contributions to mathematics and computing. One particular contribution we should mention is the Knuth-Bendix algorithm, one of the fundamental algorithms for computing with algebraic structures, particularly with groups and semigroups. This important contribution, published jointly with his student Peter B Bendix in 1970, attempts to solve solve the word problem in algebraic systems by deriving consequences of given relations to give, in some sense, a complete set. Another contribution, which has totally changed the whole way that mathematics is printed and communicated is Knuth's invention of TeX, a language for typesetting mathematical and scientific articles. Starting in 1976 Knuth took ten years off his other projects to work on the development of TeX and METAFONT, a computer software system for alphabet design.
TeX has changed the technology of mathematics and science publishing since it enables mathematicians and scientists to produce the highest quality of printing of mathematical articles yet this can be achieved simply using a home computer. However, it has not only changed the way that mathematical and scientific articles are published but also in the way that they are communicated. In the 17th century a mathematician would have written a letter to another mathematician and they would discuss their everyday lives in English, French or German, say, but whenever they came to explain a piece of mathematics they would use Latin. Nowadays mathematicians communicate by e-mail and whenever they want to explain a piece of mathematics they require mathematical symbols which almost always they communicate using TeX. Nobody, to our knowledge, has tried to measure the impact of TeX on the level of mathematical production, and indeed this would be a very difficult thing to measure, but nevertheless I [EFR] am certain that the added ease of production and communication of mathematics using TeX has had a major impact on the subject over the last ten years, say.
We should mention a few of the many further contributions by Knuth: semantics of programming languages; attribution grammar; the development of LR(k)LR(k) parsing; the Knuth-Morris-Pratt algorithm which searches for a string of characters; and structured documentation and literate programming. The work on LR(k)LR(k) parsing appeared in a 1965 paper On the translation of languages from left to right. In this paper Knuth writes:-
There has been much recent interest in languages whose grammar is sufficiently simple that an efficient left-to-right parsing algorithm can be mechanically produced from the grammar. In this paper, we define LR(k) grammars, which are perhaps the most general ones of this type, and they provide the basis for understanding all of the special tricks which have been used in the construction of parsing algorithms for languages with simple structure, e.g., algebraic languages.
The Knuth-Morris-Pratt pattern matching algorithm was published in the 1977 paper Fast pattern matching in strings. Knuth continues to publish important contributions to computer science, combinatorics and algebra, the topic of his doctoral thesis. For example in the latter area he published Efficient representation of perm groups in 1991. He writes in the introduction:-
This note presents an elementary version of C C Sims's algorithm for computing strong generators of a given perm group, together with a proof of correctness and some notes about appropriate low-level data structures.
For his quite remarkable contributions Knuth has received many honours - far too many to be mentioned in an article of this length. Let us just list a small selection. He was the first recipient of the Grace Murray Hopper Award from the Association for Computing Machinery in 1971; he was elected a Fellow of the American Academy of Arts and Science in 1973; in 1974 he won the Alan M Turing Award from the Association for Computing Machinery; he was elected to the National Academy of Sciences in 1975; in the same year he won the Lester R Ford Award from the Mathematical Association of America; he was awarded the National Science Medal in 1979 (presented to him by President Carter); he was elected to the National Academy of Engineering in 1981; he was elected an honorary member of the IEEE in 1982 and awarded their Computer Pioneer Award in the same year; he was awarded the Steele Prize for Expository Writing from the American Mathematical Society in 1986; he was awarded the Franklin Medal in 1988; he was elected to the Académie des Sciences in 1992; he was awarded the Adelskold Medal from the Swedish Academy of Sciences in 1994; he was awarded the John von Neumann Medal from the IEEE in 1995; and the Kyoto Prize from the Inamori Foundation in 1996.
Let us mention a few of the honours that Knuth has received since 2000. He has received honorary degrees from a large number of universities world-wide: Waterloo University, Canada (2000), Tübingen University (2001), the University of Oslo (2002), Antwerp University (2003), Harvard University (2003), the University of Macedonia (2003), Montreal University (2004), ETH Zürich (2005), Concordia University (2006), Wisconsin University (2006), the University of Bordeau (2007). In 2003 he was elected to the Royal Society of London, and in 2008 to the Russian Academy of Sciences. He was awarded the Gold Medal from the State Engineering University of Armenia in 2006, and in the same year the gold medal from Yerevan State University. In 2001 the minor planet "(21656) Knuth" was named after him.
In 2015 Knuth was elected to Honorary Membership of the London Mathematical Society in its 150th Anniversary year. The short citation reads:-
Professor Knuth is one of the world's greatest computer scientists, whose works have had a profound influence on the subject over the past half-century. His research covers diverse areas of mathematics and computer science, including structure in random graphs, word problems in universal algebras, pattern matching in strings, prefix codes and binary search trees.
Finally let us quote from the Stanford Magazine about Knuth's daily life following retirement:-
In retirement, he still writes several programs a week. He no longer advises students, but he hosts free public Computer Musings talks several times a year, drops in on graduate-level courses occasionally, and bikes to campus most days of the week to use the libraries or swim at the aquatic centre.

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#759 2020-07-18 00:50:20
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
725) Agnes Pockels
Agnes Luise Wilhelmine Pockels (February 14, 1862 – November 21, 1935) was a German pioneer in chemistry. Her work was fundamental in establishing the modern discipline known as surface science, which describes the properties of liquid and solid surfaces. Agnes got interested in these properties early on from washing dishes.
Early life and education
Pockels was born in Venice, Italy, in 1862. At the time, Venice was under Austrian rule, and Pockels' father served in the Austrian Army. When he fell sick, the family moved in 1871 to Brunswick, Lower Saxony, which was part of the nascent German Empire. There, Pockels attended the Municipal High School for Girls. Chemistry from her interest in science as a child. Growing up for Agnes, women were not allowed to enter universities to study. Pockels mentioned that "I had a passionate interest in natural science, especially physics, and would have liked to study“ (Agnes Pockels) in Autobiographical Notes in W. Ostwald (1932).
As a child, Pockels was interested in science, and would have liked to study physics. In those days, however, women in Germany had no access to universities. It was only through her younger brother, the physicist Friedrich Carl Alwin Pockels, that she gained access to scientific literature. Pockels studied science at home while caring for her parents.
Middle Life
Agnes Pockels younger brother Friedrich, however, also wanted to study physics and took a degree at the University of Göttingen. Friedrich would take textbooks for the university and send them to Agnes to help her study from home. Pockels published her first paper, "Surface Tension" with the help of John William Strutt, 3rd Baron Rayleigh in 1891. After this was released, her study of surface films started to take off. Later on, she continued to publish a lot of different papers and eventually recognized as a Surface science pioneer. It was known that Pockels sent a letter to Rayleigh after reading about his Results in “Naturwissenschaftliche Rundschau”. Pockels also submitted a lot of her papers to German journals while watching after her sick parents. Agnes brother, Friedrich Carl Alwin Pockels died in 1913. Later on, she realizes she had lost all contact to her field and no longer had contact with interest in her field.
Research and later life
Pockels discovered the influence of impurities on the surface tension of fluids doing the dishes in her own kitchen.She was reported to be a caretaker of her parents. Pockels spent much time cooking and cleaning with various oils, soaps, and other household products. Despite her lack of formal training, Pockels was able to measure the surface tension of water by devising an apparatus known as the slide trough, a key instrument in the new discipline of surface science. Using an improved version of this slide trough, American chemist Irving Langmuir made additional discoveries on the properties of surface molecules, which earned him a Nobel Prize in chemistry in 1932. Pockels' device is a direct antecedent of the Langmuir–Blodgett trough, developed later by Langmuir and physicist Katharine Blodgett. Pockels spent the last leg of her life caring for her sick parents which she noted to be "very challenging". During Pockels later years, she lived as an aunt known as "Auntie Agnes."
In 1891, with the help of Lord Rayleigh, Pockels published her first paper, "Surface Tension," on her measurements in the journal ‘Nature’ Thus began her career studying surface films. She never received a formal appointment, but she published a number of papers and eventually received recognition as a pioneer in the new field of surface science. Commentators wrote: "When Langmuir received the Nobel Prize for Chemistry in 1932, for his work in investigating monolayers on solids and on liquids, part of his achievement was [...] founded on original experiments first made with a button and a thin tray, by a young lady of 18 who had had no formal scientific training."
Pockels died in 1935 in Brunswick, Germany.
Honors and awards
In 1931, together with Henri Devaux, Pockels received the Laura Leonard award from the Colloid Society. In the following year, the Braunschweig University of Technology granted her an honorary PhD. Agnes Pockels primary study was with Surface science; however, she was also interested in chemistry and physics as well. Pockels was an early experimenter with surface science and physics. Pockels supposedly studied Surface tension a lot and put almost 10 years of studies into one journal. Agnes Pockels was generally interested in her studies from the "support of Lord Rayleigh and the publications in Nature." Agnes Pockels had a lot of late recognition when she was older. She was a nominee in the Annual Laura-R.-Leonard Prize. She was also the first women to win the "Dr. h. c. from the Technical University Braunschweig" on her 70th birthday.
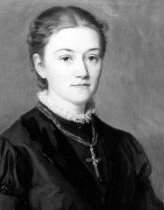
It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#760 2020-07-20 00:30:34
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
726) Gustav Kirchhoff
Gustav Kirchhoff, in full Gustav Robert Kirchhoff, (born March 12, 1824, Königsberg, Prussia [now Kaliningrad, Russia]—died October 17, 1887, Berlin, Germany), German physicist who, with the chemist Robert Bunsen, firmly established the theory of spectrum analysis (a technique for chemical analysis by analyzing the light emitted by a heated material), which Kirchhoff applied to determine the composition of the Sun.
In 1845 Kirchhoff first announced Kirchhoff’s laws, which allow calculation of the currents, voltages, and resistances of electrical networks. Extending the theory of the German physicist Georg Simon Ohm, he generalized the equations describing current flow to the case of electrical conductors in three dimensions. In further studies he demonstrated that current flows through a conductor at the speed of light.
In 1847 Kirchhoff became Privatdozent (unsalaried lecturer) at the University of Berlin and three years later accepted the post of extraordinary professor of physics at the University of Breslau. In 1854 he was appointed professor of physics at the University of Heidelberg, where he joined forces with Bunsen and founded spectrum analysis. They demonstrated that every element gives off a characteristic coloured light when heated to incandescence. This light, when separated by a prism, has a pattern of individual wavelengths specific for each element. Applying this new research tool, they discovered two new elements, cesium (1860) and rubidium (1861).
Kirchhoff went further to apply spectrum analysis to study the composition of the Sun. He found that when light passes through a gas, the gas absorbs those wavelengths that it would emit if heated. He used this principle to explain the numerous dark lines (Fraunhofer lines) in the Sun’s spectrum. That discovery marked the beginning of a new era in astronomy.
In 1875 Kirchhoff was appointed to the chair of mathematical physics at the University of Berlin. Most notable of his published works are Vorlesungen über mathematische Physik (4 vol., 1876–94; “Lectures on Mathematical Physics”) and Gesammelte Abhandlungen (1882; supplement, 1891; “Collected Essays”).

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#761 2020-07-22 01:05:46
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
727) Melissa Franklin
Melissa Eve Bronwen Franklin (born September 30, 1956) is an experimental particle physicist and the Mallinckrodt Professor of Physics at Harvard University. In 1992 Professor Franklin became the first woman to receive tenure in the Physics department at Harvard University and she served as Chair of the department from 2010 to 2014. While working at Fermi National Accelerator Laboratory in Chicago, her team found some of the first evidences for the existence of the top quark. In 1993, Franklin was elected a fellow of the American Physical Society. She is currently member of the CDF (Collider Detector at Fermilab ) (Fermilab) and ATLAS (CERN : European Organization for Nuclear Research) collaborations.
Early life and education
Franklin was born in Edmonton, Alberta and grew up first in Vancouver, British Columbia and then Toronto, Ontario, where her family moved in 1962. Her father, Stephen Franklin, was a British-born journalist who worked as drama critic for the ‘Ottawa Journal’ and later as staff writer and editor for ‘Weekend’ magazine. Her mother, Elsa, was a television producer as well as Canadian author Pierre Berton's manager and literary agent. Melissa Franklin dropped out of high school to form an alternative school with friends. After attending SEED Alternative School and the Lycee Francais Charles de Gaulle in London, she studied physics at the University of Toronto and graduated in 1977. In the summer of 1977, while Melissa Franklin was a student at CERN, she was part of a legendary bar-room bet with John Ellis which in part led to the naming of Penguin diagrams.
Career
Franklin was a student at CERN in 1978, where she met John Ellis. According to Ellis, he coined the name penguin diagrams following a bet he had made with her in a pub. Franklin earned her physics PhD from Stanford University in 1982 with a thesis titled "Selected studies of charmonium decay" under the supervision of Gary Feldman, working with the school's linear accelerator, SLAC. She did postdoctoral work at the University of California at Berkeley in the Lawrence Berkeley Laboratory. In 1988 she became an assistant professor at the University of Illinois, and worked at Fermilab in Chicago. In 1987 she joined Harvard University, later becoming the physics department's first tenured woman professor. For over a decade, Franklin traveled between Boston and Chicago every few weeks, to check on and fix equipment at Fermilab. In 1995, her team proved the existence of the top quark.
At Harvard, Franklin co-directs the Laboratory for Particle Physics and Cosmology (LPPC), alongside Gary Feldman, John Huth, Masahiro Morii and Christopher Stubbs. The LPPC studies topics on the Energy Frontier, the Intensity Frontier and the Cosmic Frontier.
Since the 1990s, Franklin has been a frequent guest on the CBC Radio science program ‘Quirks and Quarks.’ Franklin has also been a frequent lecturer and "dramatic read[er]" in the annual Ig Noble Prize Ceremonies and other events of the ‘Annals of Improbable Research’.
(The Ig Nobel Prize is a satiric prize awarded annually since 1991 to celebrate ten unusual or trivial achievements in scientific research, its stated aim being to "honor achievements that first make people laugh, and then make them think.")

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#762 2020-07-24 00:22:29
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
728) George de Hevesy
George de Hevesy (Full name : George Charles de Hevesy) was born in Budapest on August 1st, 1885, the son of Louis de Hevesy, Court Counsellor and Eugénie, née Baroness Schosberger. After matriculating at the Gymnasium of the Piarist Order in 1903 he studied at Budapest University and Berlin Technical University and he gained his doctor’s degree at the University of Freiburg im Breisgau in 1908. He worked for two years as an assistant at the Institute of Physical Chemistry, Technical University of Switzerland before having a short spell with Professor Fritz Haber when he was able to witness much of the fundamental work of Haber and Rossignol on ammonia synthesis. He travelled to England in 1910 to study under Professor Ernest Rutherford at Manchester. He interrupted early in 1913 his studies to carry out jointly with Frederic Paneth the first radioactive-tracer experiment at the Vienna Institute of Radium Research. During his stay in Vienna he obtained the Venia Legendi in the University of Budapest. In 1915 he was drafted into the Austrian-Hungarian Army. After the end of the war he was teaching for 6 months in the University of Budapest and left the spring of 1919 for Copenhagen to discuss his future activities at Niels Bohr‘s Institute which was to be erected. In 1920 he settled in Copenhagen.
Six years later he returned to Freiburg as Professor of Physical Chemistry. In 1930 he was appointed Baker Lecturer at Cornell University, Ithaca. Four years later he took up again his activities at Niels Bohr’s Institute which he terminated in 1952. He was domiciled in Stockholm since 1943 and was an Associate of the Institute of Research in Organic Chemistry. In 1949 he was elected Franqui Professor in the University of Ghent. In his retirement, he remains an active scientific associate of the University of Stockholm.
His early investigations involved a study of the chemical behaviour of molten salts and his introduction to practical radiochemistry came in Rutherford’s laboratories at Manchester. His work there, and later in Vienna and Budapest, mainly concerned the investigation and use of radium and lead isotopes.
In Copenhagen, de Hevesy’s researches were initially concerned with isotopic separations and in 1923, together with Coster, he discovered the element hafnium. He was responsible for pioneer work in the use of isotopic indicators both in inorganic and life sciences and later, in Freiburg, he was involved in the first clinical use of isotopes. On his return to Copenhagen, he demonstrated the formation of new artificially radioactive isotopes and subsequently introduced a method of activation analysis based on neutron bombardment of the element to be investigated. This method was to replace X-ray analysis with fluorescent X-rays which he introduced during his stay in Freiburg. The year 1934 saw the beginning of numerous investigations in the field of plant and animal physiology, using labelled atoms: these researches were supported by generous grants made by the Carlsberg Foundation, the Rask-Ørsted Foundation, the Rockefeller Foundation and others. His work in Sweden has continued on the same lines and he has studied, amongst other things, the effect of X-rays on the formation of nucleic acid in tumours and in normal organs, and iron transport in healthy and cancerous organisms; this work is supported by the Swedish State Research Council and the Wallenberg Foundation.
Professor de Hevesy is the author of several important books on radiochemistry and his many scientific papers are valuable and accurate records of devoted work. He was awarded the Cannizaro Prize (Academy of Sciences, Rome) in 1929, he was the Copley Medallist (Royal Society, London) in 1949, Faraday Medallist in 1950, Baily Medallist in 1951 and Silvanus Thompson Medallist in 1955. In 1959 he received the Ford Foundation’s Atoms for Peace Award Medal, in 1961 the Niels Bohr Medal and the Rosenberger Medal of the University of Chicago. Honorary degrees conferred upon Professor de Hevesy include Doctor of Philosophy, Uppsala, Freiburg, and Copenhagen; Doctor of Science, Ghent, Liège, London, and Capetown; and Doctor of Medicine, São Paulo, Rio de Janeiro, Turin, and Freiburg. He is a Fellow of the Royal Society (London), the Swedish Academy of Sciences, Gothenburg Academy, and eleven other scientific academies. He is Honorary Fellow of the Chemical Society (London), the Royal Institution (London), the British Institute of Radiology, the Finnish Chemical Society, the German Bunsen Society, the German Physiological Society, the Chemical Society of Japan, and the American Society of Nuclear Medicine. In addition, he holds honorary memberships of many more learned societies.
Professor de Hevesy married Pia Riis in 1924. They have one son and three daughters.
George de Hevesy died on July 5, 1966.

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#763 2020-07-26 00:18:33
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
729) Henri-Victor Regnault
Henri-Victor Regnault, (born July 21, 1810, Aix-la-Chapelle, Fr.—died Jan. 19, 1878, Auteuil), French chemist and physicist noted for his work on the properties of gases.
After studying with Justus von Liebig, in Giessen, Regnault became professor of chemistry successively at the University of Lyon, the École Polytechnique (1840), and the Collège de France (1841). His four-volume work on chemistry appeared in 1847. While director of the porcelain factory at Sèvres (from 1854), he continued his work in science. During the Franco-German War (1870–71) his laboratory there was destroyed, and his son Henri, the painter, was killed.
Regnault designed apparatus for a large number of physical measurements and carefully redetermined the specific heats of many solids, liquids, and gases. He showed that no two gases have precisely the same coefficient of expansion and proved that Boyle’s law of the elasticity of a “perfect gas” is only approximately true for real gases. In introducing his air thermometer he determined the absolute expansion of mercury. He also devised a hygrometer.
Prof Henri Victor Regnault (21 July 1810 – 19 January 1878) was a French chemist and physicist best known for his careful measurements of the thermal properties of gases. He was an early thermodynamicist and was mentor to William Thomson in the late 1840s. He never used his first given name, and was known throughout his lifetime as Victor Regnault.
Biography
Born in Aix-la-Chapelle in 1810 (modern Aachen, Germany and at that time under French rule), he moved to Paris at the age of eight, following the death of his parents. There, he worked for an upholstery firm until he was eighteen. In 1830, he was admitted to the École Polytechnique, and in 1832 he graduated from the École des mines.
Working under Justus von Liebig at Gießen, Regnault distinguished himself in the nascent field of organic chemistry by synthesizing several chlorinated hydrocarbons (e.g. vinyl chloride polyvinylidene chloride, dichloromethane), and he was appointed professor of chemistry at the University of Lyon. In 1840, he was appointed the chair of chemistry of the École Polytechnique, and in 1841, he became a professor of Physics in the Collège de France.
Beginning in 1843, he began compiling extensive numerical tables on the properties of steam. These were published in 1847, and led to his receiving the Rumford Medal of the Royal Society of London and appointment as Chief Engineer of Mines. In 1851 he was elected a foreign member of the Royal Swedish Academy of Sciences. In 1854 he was appointed director of the porcelain works at Sèvres, the ‘Manufacture nationale de Sèvres’.
At Sèvres, he continued work on the thermal properties of matter. He designed sensitive thermometers, hygrometers, hypsometers and calorimeters, and measured the specific heats of many substances and the coefficient of thermal expansion of gases. In the course of this work, he discovered that not all gases expand equally when heated and that Boyle's Law is only an approximation, especially at temperatures near a substance's boiling point.
Regnault was also an avid amateur photographer. He introduced the use of pyrogallic acid as a developing agent, and was one of the first photographers to use paper negatives. In 1854, he became the founding president of the Société française de photographie.
In 1871, his laboratory at Sèvres was destroyed and his son Alex-Georges-Henri Regnault killed, both as a result of the Franco-Prussian War. He retired from science the next year, never recovering from these losses.
Legacy
The crater Regnault on the Moon is named after Regnault, and his name is one of the 72 names inscribed on the Eiffel Tower. Some have suggested that the symbol R for the ideal gas constant is also named after him.
He was the first president of Société française de photographie.
The French Lagrange-class submarine Regnault, built between 1913 and 1924 was named for him.

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#764 2020-07-28 01:37:37
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
730) Lene Vestergaard Hau
Lene Vestergaard Hau, (born Nov. 13, 1959, Vejle, Den.), Danish physicist who pioneered the use of Bose-Einstein condensates in slowing and stopping light.
From an early age Hau enjoyed mathematics, and she excelled at school, skipping the 10th grade. Her father, who ran a heating business, and her mother, a shop clerk, encouraged her in her scientific pursuits. Hau entered Aarhus University in Aarhus, Den., where she was drawn to studying physics because of her interest in mathematics and quantum mechanics. There she earned a bachelor’s degree in mathematics (1984), a master’s degree in physics (1986), and a doctorate in physics (1991). Her studies included nine months at the European Organization for Nuclear Research (CERN) in Geneva in 1984–85. In 1989 she accepted a postdoctoral position on the faculty of Harvard University, where in 1999 she became the Gordon McKay Professor of Applied Physics. Hau also took a position at the Rowland Institute in 1991, serving as principal investigator for the Atom Cooling Group until 1999. Though she resided in the United States, Hau retained her Danish citizenship.
In 1994, working with Jene A. Golovchenko at the Rowland Institute, Hau developed one of the first elements that led to the slowing of light. Called a “candlestick,” the device wicked sodium atoms out of molten sodium metal and projected them into a cooling apparatus that used lasers to cool the atoms to a temperature 50 billionths of a degree above absolute zero. In a 1999 experiment Hau and her colleagues at the Rowland Institute shone lasers through a cloud of ultracold sodium atoms—known as a Bose-Einstein condensate - which effectively slowed light from its normal speed of about 299,792 km (186,282 miles) per second to 61 km (38 miles) per hour.
In 2001 Hau and her team of physicists at the Rowland Institute published a paper in which they described how they had sent a pulse of laser light into a Bose-Einstein condensate, halted the light, stored it for a fraction of a second, and then released it. That year Hau was selected for a five-year MacArthur Fellowship. She was named Mallinckrodt Professor of Physics and of Applied Physics at Harvard in 2006. By 2007 she and her team had managed to convert a pulse of light into a matter wave by passing it through a Bose-Einstein condensate, and then reconvert it to light by passing it through another Bose-Einstein condensate. It was believed that these advances could translate into practical applications that would substantially improve telecommunications and computers.
Hau was elected to the Royal Danish Academy of Sciences in 2002, the Royal Swedish Academy of Sciences in 2008, and the American Academy of Sciences in 2009.

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#765 2020-07-30 00:23:52
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
731) May-Britt Moser
May-Britt Moser, (born January 4, 1963, Fosnavåg, Norway), Norwegian neuroscientist who contributed to the discovery of grid cells in the brain and the elucidation of their role in generating a system of mental coordinates by which animals are able to navigate their environment. Moser’s work enabled scientists to gain new insight into cognitive processes (such as memory) and spatial deficits associated with human neurological conditions such as Alzheimer disease. For her discoveries concerning the neural systems that underlie spatial representation in the mammalian brain, she was awarded the 2014 Nobel Prize for Physiology or Medicine, which she shared with her husband, Norwegian neuroscientist Edvard I. Moser, and with British-American neuroscientist John O’Keefe. The Mosers were the fifth married couple to share a Nobel Prize.
May-Britt grew up on a farm in the remote western region of Norway. In the early 1980s she attended the University of Oslo, where she studied multiple subjects, including mathematics, neurobiology, and psychology. She married Edvard in 1985, and together they decided to pursue the study of brain-behaviour relationships. In the early 1990s May-Britt undertook graduate studies at Oslo, working alongside her husband in the laboratory of Norwegian researcher Per Oskar Andersen. She investigated correlations between the anatomical structure of the hippocampus and spatial learning in rats, work that culminated in a doctorate degree in neurophysiology in 1995. Over the course of the next year, she and Edvard traveled to the University of Edinburgh to study with British neuroscientist Richard Morris and to University College London, where they spent time in O’Keefe’s laboratory. In 1996 May-Britt accepted an assistant professorship at the Norwegian University of Science and Technology (NTNU), where Edvard also had been offered a position. Both were later made full professors at NTNU.
The Mosers investigated the neural networks of the hippocampus, attempting to identify the mechanism underlying the generation of cortical (spatial) maps. They began by examining the effects of hippocampal lesions on the activity of place cells, which had been reported by O’Keefe and his student Jonathan O. Dostrovsky in 1971 to function in cortical mapping. The Mosers’ observations drew their attention to a part of the brain known as the entorhinal cortex, which shared direct connections with CA1, an area of the hippocampus that O’Keefe and Dostrovsky had shown to play a key role in spatial processing. With the assistance of Dutch functional neuroanatomist Menno P. Witter, the Mosers were able to precisely place electrodes in the dorsocaudal medial entorhinal cortex (dMEC) of the rat brain, allowing them to record the activity of cells in response to specific behaviours. Similar to O’Keefe’s findings with place cells, the Mosers found that cells in the dMEC became active in relation to an animal’s position in its environment. But, unlike the activity of place cells, the activity of the cells that the Mosers observed occurred in a strikingly regular pattern: as rats ran freely in their enclosures, spikes of activity at each electrode were not only evenly spaced but also similar in direction and size. The regular activity formed a grid of equilateral, tessellating triangles, as revealed by spatial analyses, which inspired the name grid cell.
In later work, the Mosers discovered additional cells in the dMEC that signaled spatial information, including head direction cells, which fired preferentially in response to an animal’s head direction, and border cells, which transmitted information about the boundaries of an animal’s environment. They also found that grid cells, head direction cells, and border cells interacted with place cells in the hippocampus to determine orientation and navigation. The spatial representation system was described as an “inner GPS.”
May-Britt was a founding codirector, with Edvard, of the Kavli Institute for Systems Neuroscience in 2007 and the Centre for Neural Computation in 2013, both at NTNU. She was a recipient of multiple awards, notably the 2013 Louisa Gross Horwitz Prize for Biology or Biochemistry (shared with Edvard and O’Keefe), in addition to the Nobel Prize.

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#766 2020-08-01 00:35:15
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
732) Hendrika Johanna van Leeuwen
Hendrika Johanna van Leeuwen (July 3, 1887 – February 26, 1974) was a Dutch physicist known for her early contributions to the theory of magnetism. She studied at Leiden University under the guidance of Hendrik Antoon Lorentz, obtaining her doctorate in 1919. Her thesis explained why magnetism is an essentially quantum mechanical effect, a result now referred to as the Bohr–van Leeuwen theorem. (Niels Bohr had arrived at the same conclusion a few years earlier.) She continued to investigate magnetic materials at the "Technische Hogeschool Delft" (now called the Delft University of Technology), first as "assistant" between September 1920 and April 1947, and then she was promoted to "lector in de theoretische en toegepaste natuurkunde" (reader in theoretical and applied physics).
Hendrika van Leeuwen was the sister-in-law of Gunnar Nordström, known as the "Einstein of Finland", who studied in Leiden with Paul Ehrenfest, the successor of Lorentz. Her sister Cornelia (Nel) also started a PhD in Leiden, under Willem Keesom, but stopped when she married Nordström and moved with him to Helsinki.
Van Leeuwen was present at the celebration of the golden anniversary of the doctorate of Lorentz, on 11 December 1925, and on that occasion reported on the role of Lorentz as scientist and teacher.
.
It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#767 2020-08-03 00:31:20
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
733) Carl David Anderson
Carl David Anderson, who was born of Swedish parents – his father was Carl David Anderson and his mother Emma Adolfina Ajaxson – in New York City (USA) on 3rd September, 1905, has spent the bulk of his life in the United States. He graduated from the California Institute of Technology in 1927 with a B.Sc. degree in Physics and Engineering, and was awarded his Ph.D. degree by the same Institute, in 1930. For the period 1930-1933 he was Research Fellow there, subsequently (1933) Assistant Professor of Physics, and Professor of Physics (1939) During the war years (1941-1945) he was also active on projects for the National Defence Research Committee and the Office of Scientific Research and Development.
His early researches were in the field of X-rays. For his doctoral thesis he studied the space distribution of photoelectrons ejected from various gases by X-rays. In 1930, with Professor Millikan, he began his cosmic-ray studies which led in 1932 to the discovery of the positron. He has studied the energy distribution of cosmic-ray particles and the energy loss of very high speed electrons in traversing matter. In 1933 he and Dr. Neddermeyer obtained the first direct proof that gamma rays from ThC” generate positrons in their passage through material substances. Since 1933 he has continued his work on radiation and fundamental particles. Most of Anderson’s researches and discoveries have been published in ‘The Physical Review and Science’.
Among the scientific honours bestowed upon him, in addition to the Nobel Prize, may be mentioned the following: Gold Medal of the American Institute of City of New York (1935); Sc.D. of Colgate University (1937); Elliott Cresson Medal of the Franklin Institute (1937); Presidential Certificate of Merit (1945); LL.D. Temple University (1949); John Ericsson Medal of the American Society of Swedish Engineers (1960).
In 1946 Anderson married Lorraine Bergman; they have two sons, Marshall and David.
Carl D. Anderson died on January 11, 1991.

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#768 2020-08-05 00:33:51
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
734) Rózsa Péter
Rózsa Péter, born Rózsa Politzer, (17 February 1905 – 16 February 1977) was a Hungarian mathematician and logician. She is best known as the "founding mother of recursion theory".
Hungarian Mathematician : 1905–1977
A pioneering theorist of a mathematical discipline with important applications in computer science, Rózsa Politzer was born February 17, 1905, in Budapest, Hungary. Although she never married, Politzer changed her name to Rózsa Péter in 1930. Initially, Péter intended to fulfill her father's wish for her to become a chemist, but lectures by mathematicians enticed her to a course that would change her life as well as the field of mathematics. Through lectures and papers in the 1930s, she promoted the study of recursive functions as a distinct field of mathematics. This aspect of number theory considers functions that are used to study the structure of number classes or functions in terms of the complexity of the calculations required to determine them. Since theories of relay contact systems , cybernetics , and computer programming are dependent on recursive functions, Péter's work is indispensable to computer science.
After attending the Mária Terézia Girls' School in Budapest, Péter enrolled at Eötvös Loránd University in 1922 to pursue a career in chemistry. Soon after starting, however, she decided to change her field of study to mathematics. Also while in school, she met László Kalmár, with whom she maintained a close, lifelong professional friendship. Kalmár, who became a famous mathematics pioneer in his own right, was the person who later introduced her to recursive functions.
In 1932 Péter wrote a paper on recursive functions. She lectured on the subject at the International Congress of Mathematicians in Zurich in 1932 and again in 1936. At this conference, she was the first to formally suggest recursive mathematics as a field unto itself. In 1935, she received her Ph.D. summa cum laude from Eötvös Loránd University. After publishing several papers on recursive functions, she was invited to join the editorial boards of several international mathematical journals, including, in 1937, the ‘Journal of Symbolic Logic.’
In 1943 Péter wrote ‘Playing with Infinity: Mathematical Explorations and Excursions’ (not released until 1945 because of World War II), a work intended for the general public. It discussed number theory, geometry, calculus, logic, and Gödel's undecidability theory, all in a manner accessible to nonspecialists. This book successfully attempted to bridge the gap between mathematics and science and the humanities. Péter's work has since been translated into forty languages.
After Germany's 1945 defeat in World War II, Péter enjoyed teaching at Pedagógiai Förskola, a teacher's college in Budapest, for the next ten years. In 1951 she published ‘Recursive Functions’, the first book on recursive functions. This book was also translated into numerous other languages and became a standard reference. In 1955 the teacher's college was shut down. Péter became a professor of mathematics at Eötvös Loránd University in Budapest. Her interests turned to the use of recursive functions and their relevance to computers. Her first paper on this subject addressed primitive recursive functions and ALGOL . After her retirement, she continued her research into recursive functions and their relationship to computer program languages. She published her last book, ‘Recursive Functions in Computer Theory’, in 1976.
Péter was awarded the Kossuth Prize in 1951 by the state of Hungary for her achievements. She also received the State Award, Silver Degree, in 1970, and the State Award, Gold Degree, in 1973. That same year, she became a corresponding member and the first female member of the Hungarian Academy of Sciences. She was made an honorary president of the János Bolyai Mathematical Association in 1975.
In addition to the study of recursive mathematics, Péter was very active in mathematics education, writing textbooks and teaching both children and mathematics teachers. Péter challenged society, and particularly children, to see mathematics and the sciences as entertaining, joyful, adventurous, and ultimately more than dry, intellectual exercises. She believed mathematics to be an indispensable part of science, and science to be an indispensable part of humanity.
Péter's interests extended beyond mathematics; she enjoyed art and cooking and also wrote theater reviews. She enjoyed literature as well and translated poetry into Hungarian. However, mathematics remained her first love, and in ‘Playing with Infinity’, she wrote: "I love mathematics not only for its technical applications, but principally because it is beautiful: because man has breathed his spirit of play into it, and because it has given him his greatest game—the encompassing of the infinite." Péter died of cancer on February 17, 1977.
(Computability theory, also known as recursion theory, is a branch of mathematical logic, of computer science, and of the theory of computation that originated in the 1930s with the study of computable functions and Turing degrees. The field has since expanded to include the study of generalized computability and definability. In these areas, recursion theory overlaps with proof theory and effective descriptive set theory.
Basic questions addressed by recursion theory include:
• What does it mean for a function on the natural numbers to be computable?
• How can noncomputable functions be classified into a hierarchy based on their level of noncomputability?
Although there is considerable overlap in terms of knowledge and methods, mathematical recursion theorists study the theory of relative computability, reducibility notions, and degree structures; those in the computer science field focus on the theory of subrecursive hierarchies, formal methods, and formal languages.)

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#769 2020-08-07 00:34:35
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
735) Berta Karlik
Berta Karlik was an Austrian physicist. She worked for the University of Vienna, eventually becoming the first female professor at the institution. While working with Ernst Foyn she published a paper on the radioactivity of seawater. She discovered that the element 85 astatine is a product of the natural decay processes. The element was first synthesized in 1940 by Dale R. Corson, K. R. MacKenzie, and Emilio Segrè, after several scientists in vain searched for it in radioactive minerals.
Biography
Early life and education
Berta Karlik was born in Vienna to an upper-class family and was home-taught for her elementary education. While being taught at home she learned to play the piano as well as speak and write French, Dutch and English. From 1919 to 1923 she attended the Reform-Realgymnasium and upon graduating in 1923 she was accepted as a regular student to the Philosophical Faculty at the University of Vienna until 1928 when she received her Ph.D.
While enrolled as a student at the university Karlik became an essential member of Hans Pettersson's research group at the Radium Institute with her specialty being the scintillation counter. Karlik also attended a fellowship from the International Federation of University Women which required her to travel while working for the Radium Institute.
After receiving her degree in Physics Karlik accepted a teaching position at the Realgymnasium in Vienna, where she was a former pupil.
Entering the Field
In 1930 Karlik found a job at a laboratory run by William Bragg in London. Here she worked on crystallography and used X-rays to study the structure of crystals. Karlik's knowledge of radiophysics attracted the attention of noted crystallographers Ellie Knaggs and Helen Gilchrist. The same year that she formed a group with these two women is the same year she first visits Marie Curie's lab in Paris which signaled the start of her long correspondence with various other female physicists.
While Karlik occasionally sent letters to Marie Curie she kept regular correspondence with other notable physicists such as Ellen Gleditsch and Eva Resmtedt, two of the Curie researchers, as well as Lise Meitner, with whom Karlik was quite close during her life. Throughout her life she would meet with Meitner who worked with the team responsible for discovering nuclear fission.
Research
After studying in Paris and London she started working at the Institut für Radiumforschung (Institut for Radium Research) in Vienna in 1931. From 1937 she was allowed to give lectures, and slowly advanced in the hierarchy of the institute.
Simultaneously Karlik joined a group on seawater research headed by the Swedish physicist Hans Pettersson. Mixing knowledge of oceanography and radioactivity, Karlik helped to bring up concerns about the biological issue of uranium contamination of seawater.
During the Second World War she made her most important discovery, that the element with the atomic number 85, Astatine, was a product of natural decay. Astatine's main use is in radiotherapy to kill cancer cells. Due to this discovery Karlik was awarded the Haitinger Prize for Chemistry from the Austrian Academy of Sciences in 1947.
She became provisional director of the institute in 1945 and official in 1947 upon discovering the existence of astatine. Berta Karlik was the first woman to be full professor ("ordentliche Professur") at the University of Vienna in 1956. She retired in 1973, but worked at the institute till her death in 1990.
Publications
• "An Alpha-Radiation Ascribed to Element 85," S.B.Akad. Wiss. Wien, 152:Abt. IIa (Nos. 6-10) 103-110(1943), with T. Bernert.
• "Element 85 in the Natural Disintegration Series," Z. Phys., 123: (Nos. 1-2) 51-72 (1944), with T. Bernert.
• "Uranium Content of Seawater," Akad. Wiss. Wien, Ber, 144:2a (Nos.5-6) 217-225 (1935), with F. Hernegger.

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#770 2020-08-09 00:30:19
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
736) Christiane Nüsslein-Volhard
Christiane Nüsslein-Volhard, (born October 20, 1942, Magdeburg, Germany), German developmental geneticist who was jointly awarded the 1995 Nobel Prize for Physiology or Medicine with geneticists Eric F. Wieschaus and Edward B. Lewis for their research concerning the mechanisms of early embryonic development. Nüsslein-Volhard, working in tandem with Wieschaus, expanded upon the pioneering work of Lewis, who used the fruit fly, or vinegar fly (‘Drosophila melanogaster’), as an experimental subject. Her work has relevance to the development of all multicellular organisms, including humans.
At Eberhard-Karl University of Tübingen, Nüsslein-Volhard received a diploma in biochemistry in 1968 and a doctorate in genetics in 1973. After holding fellowships in Basel and Freiburg, she joined Wieschaus as a group leader at the European Molecular Biology Laboratory in Heidelberg in 1978. In 1981 she returned to Tübingen, where she served as director of the Max Planck Institute for Developmental Biology from 1985 to 2015.
At Heidelberg, Nüsslein-Volhard and Wieschaus spent more than a year crossbreeding 40,000 fruit fly families and systematically examining their genetic makeup at a dual microscope. Their trial-and-error methods resulted in the discovery that of the fly’s 20,000 genes, about 5,000 are deemed important to early development and about 140 are essential. They assigned responsibility for the fruit fly’s embryonic development to three genetic categories: gap genes, which lay out the head-to-tail body plan; pair-rule genes, which determine body segmentation; and segment-polarity genes, which establish repeating structures within each segment.
In the early 1990s Nüsslein-Volhard began studying genes that control development in the zebra fish ‘Danio rerio’. These organisms are ideal models for investigations into developmental biology because they have clear embryos, have a rapid rate of reproduction, and are closely related to other vertebrates. Nüsslein-Volhard studied the migration of cells from their sites of origin to their sites of destination within zebra fish embryos. Her investigations in zebra fish have helped elucidate genes and other cellular substances involved in human development and in the regulation of normal human physiology.
In addition to the Nobel Prize, Nüsslein-Volhard received the Leibniz Prize (1986) and the Albert Lasker Basic Medical Research Award (1991). She also published several books, including ‘Zebrafish: A Practical Approach’ (2002; written with Ralf Dahm) and ‘Coming to Life: How Genes Drive Development’ (2006).

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#771 2020-08-11 00:53:10
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
737) Yvonne Brill
Yvonne Brill, (Yvonne Madelaine Claeys), Canadian-born American rocket scientist (born Dec. 30, 1924, St. Vital, Man.—died March 27, 2013, Princeton, N.J.), pioneered the electrothermal hydrazine thruster—a more fuel-efficient rocket thruster designed to keep communications satellites from slipping out of orbit. Brill was not admitted to the men-only engineering department at the University of Manitoba, but she graduated (1945) at the top of her class with degrees in chemistry and mathematics. (She later received a master’s degree [1951] in chemistry from the University of Southern California.) Despite her lack of an engineering degree, she was recruited (1945) by Douglas Aircraft (which became the basis for the RAND Corporation) in Santa Monica, Calif., to help create the first designs for an American satellite. Throughout that period she was believed to be the only woman in the U.S. conducting research in the field of rocket science. Brill put her career on hold in the late 1950s to stay home with her children, but she returned (1966) to work full-time for RCA’s rocket subsidiary, where she developed the thruster that rapidly became the industry standard. She also was involved in developing the Nova rockets that were used in American Moon missions; Tiros, the first weather satellite; the Atmosphere Explorer, the first upper-atmosphere satellite; and the Mars Observer satellite (1992). While working (1981–83) for NASA, she contributed to the development of a rocket engine for the space shuttle. Brill received numerous awards for her groundbreaking work, and in 2010 she was inducted into the National Inventors Hall of Fame.
Yvonne Madelaine Brill (née Claeys; December 30, 1924 – March 27, 2013) was a Canadian-American rocket and jet propulsion engineer. She is responsible for inventing the fuel-efficient rocket thruster that keeps satellites in orbit today. During her career she was involved in a broad range of national space programs in the United States, including NASA and the International Maritime Satellite Organization.
Early life
Brill was born in Winnipeg, Manitoba, Canada. Her parents were immigrants from Belgium, making her and her two siblings first-generation Canadians. While she was in high school, one of her teachers told her that a woman wouldn't get anywhere in science. Her father wanted her to stay at home and open a little shop in town[4]. She definitely did not listen to them. She attended the University of Manitoba, but was barred from studying engineering because of her gender, so she studied chemistry and mathematics. She graduated at the top of her class in 1945 with a bachelor's degree in chemistry and mathematics. She went on to study at the University of Southern California, where she took night classes and graduated in 1951 with a master's degree in chemistry.
Career
Brill's work in satellite propulsion systems resulted in a number of significant developments. She developed the concept for a new rocket engine, the hydrazine resistojet, and proposed the use of a single propellant because of the value and simplicity that it would provide. Her invention resulted in not only higher engine performance, but also increased the reliability of the propulsion system. The reduction in propellant weight requirements enabled either increased payload capability or extended mission life.
Brill was believed to be the only woman in the United States researching rocket science in the 1940s. In 1945 she was recruited by Douglas Aircraft despite her lack of a degree in engineering to help develop the first American satellites. She put her career on hold in the 1950s to stay at home and raise her children. Then in 1966 she returned to the field, where she rejoined the Radio Corporation of America (RCA).
Brill invented the hydrazine resistojet propulsion system in 1967, for which she holds U.S. Patent No. 3,807,657. Her invention became a standard in the industry and has translated into millions of dollars of increased revenue for commercial communications satellite owners.
Brill contributed to the propulsion systems of TIROS, the first weather satellite; Nova, a series of rocket designs that were used in American Moon missions; Explorer 32, the first upper-atmosphere satellite; and the Mars Observer, which in 1992 almost entered a Mars orbit before losing communication with Earth.
Awards and honors
Brill was awarded the AIAA Wyld Propulsion Award (2002) and the American Association of Engineering Societies John Fritz Medal (2009). In 1980, Harper's Bazaar and the DeBeers Corporation gave her their Diamond Superwoman award for returning to a successful career after starting a family. In 2001 she was awarded the NASA Distinguished Public Service Medal.[10] In 2010 President Barack Obama presented her with the National Medal of Technology and Innovation. In 2010 she was also inducted into the National Inventors Hall of Fame.
She was elected to the National Academy of Engineering in 1987. She was named fellow of The Society of Women Engineers (SWE) in 1985 and received its highest honor, the Achievement Award, the following year.
The Yvonne C. Brill Lectureship of the American Institute of Aeronautics and Astronautics (AIAA) is named in her honor and presented annually.
As her life dwindled down, she spent the last twenty years promoting women in science and engineering and nominated them for awards and prizes she thought they deserved.
Death
A longtime resident of the Skillman section of Montgomery Township, New Jersey, United States, Brill died of complications of breast cancer in Princeton, New Jersey.
An obituary of Brill published in the March 30, 2013 issue of the New York Times originally began: "She made a mean beef stroganoff, followed her husband from job to job and took eight years off from work to raise three children". The obituary was heavily criticized for leading with and overemphasizing Brill's gender and family life, rather than her scientific and career accomplishments and was cited as an example of an article that failed the Finkbeiner test. The Times later dropped the reference to her cooking and changed the lead of the article.

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#772 2020-08-13 00:14:19
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
738) John Kemeny
John Kemeny, in full John George Kemeny, (born May 31, 1926, Budapest, Hungary—died December 26, 1992, Hanover, New Hampshire, U.S.), Hungarian-born American mathematician and computer scientist. He emigrated to the U.S. with his family at age 14. He took a year off from his undergraduate studies at Princeton University to work on the Manhattan Project and was later a research assistant to Albert Einstein. He received a Ph.D. in 1949 and joined the Dartmouth College faculty in 1953, where he worked to develop the mathematics department. In the mid-1960s he and Thomas E. Kurtz (born 1928) developed the BASIC computer programming language. He was a pioneer in the promotion of “new math” and the use of computers in education. He served as president of Dartmouth (1970–81).
Born May 31, 1926, Budapest, Hungary; died December 26, 1992, Lebanon, N.H.; president of Dartmouth College, mathematician who was an assistant to Albert Einstein, chair of the Three Mile Island investigative committee, with Thomas Kurtz, invented the programming language BASIC.
Education: BA, mathematics, Princeton University, 1947; PhD, mathematics, Princeton University, 1949.
Professional Experience: assistant, Theoretical Division, Los Alamos Project, 1945-1948; Princeton University: research assistant, [Assistant to Albert Einstein.] Institute for Advanced Study, 1948-1949, Fine Instructor and ONR fellow, 1949-1951, assistant professor of philosophy, 1951-1953; Dartmouth College: professor of mathematics, 1953-1990, chairman, Department of Mathematics, 1955-1967, Albert Bradley Third Century Professor, 1969, president, 1970-1981; vice chairman, National Science Foundation Advisory Committee; member, National Research Council,
Honors and Awards: Between 1965 and 1989 he received honorary degrees from 20 universities, including Princeton University; Priestley Award, Dickinson College, 1976; IEEE Computer Society Pioneer Award, 1985; AFIPS Education Award, 1983; New York Academy of Sciences Award, 1984; fellow, American Academy of Arts and Sciences; First Louis Robinson Lifetime Achievement Award, EDUCOM, 1990.
John Kemeny came to the US in 1940 and was naturalized in 1945. He worked on the Los Alamos Project during World War II, and then completed his bachelor's and doctorate degrees at Princeton University, working with Albert Einstein. After several years as a faculty member at Princeton and Dartmouth College, he was elected president of Dartmouth College, serving 11 years. Kemeny and Thomas Kurtz co-invented and developed the Dartmouth Time-Sharing System (DTSS) and created the programming language BASIC to provide computing access to a broad spectrum of undergraduate students. The language has continued to develop and is perhaps the most widely used language, at least among younger and nonprofessional users; for many it is the first programming language learned. His citation for the first 1983 AMPS Education Award recognized Kemeny for "his visionary efforts at making computing universal for students of all disciplines."
John Kemeny was born in Budapest on May 31, 1926. [Edited with permission from Internet posting by Jay Robert Hauben on Newsgroups: alt.amateur-comp, comp.lang.misc, alt.1ang.basic, sci.misc, and comp.misc. May 31, 1993. Also reprinted with permission from The Amateur Computerist, Vol. 5, No. 1-2, May 1, 1993.] His education and intellectual development in Hungary must have been very impressive, but in 1940, to escape the Nazi tide, his family emigrated to New York City. Kemeny entered high school knowing virtually no English. He graduated three years later, first in his class, and was accepted at Princeton University to study mathematics.
By the time Kemeny turned 18, he had finished his first year at Princeton. He was immediately drafted and sent to Los Alamos to be a "computer," one of 20 operators who used 17 IBM bookkeeping calculators to get numerical solutions to differential equations connected with the design of the atom bomb. It took two or three weeks, working three 8-hour shifts, six days per week, to get one result. The calculators were fed punched cards, which were moved manually from machine to machine. Between calculations, the plug boards had to be rewired by hand. At the end of a cycle, the calculation was summarized on a printout which had to be checked by eye for "catastrophes." If any were found, the cycle had to be repeated. Years later, Kemeny was to note that one undergraduate working one afternoon, using a 1970 timesharing computer, could solve as many differential equations as the whole Los Alamos team did in a whole year. And there could be 100 other users on the computer at the same time.
While at Los Alamos, Kemeny heard a lecture by fellow Hungarian born John von Neumann, who was a consultant to the "computer operation." Von Neumann proposed a fully electronic computer based on a binary number system, with internal memory for both data and a stored program. To Kemeny and the other "computers," von Neumann's machine sounded like a dream. Kemeny wondered if he would live long enough to ever use one.
After the war, Kemeny returned to Princeton. In 1948-1949, while finishing his dissertation, Kemeny served as Albert Einstein's research assistant at the Institute for Advanced Study. Von Neumann was at the institute also, working on the machine he had described in his lecture two years earlier. Einstein and Kemeny crossed paths with von Neumann occasionally and had some long conversations concerning symbol-handling (as opposed to number-handling) computers.
Kemeny finished his PhD and stayed at Princeton, teaching mathematics and philosophy until 1953. During his time at Princeton, his contact with von Neumann and his computer had a deep effect on Kemeny. Here was the brilliant mathematician playing around with the nuts and bolts of a computing machine and raising profound philosophical questions about the relation between humans and machines. In a Scientific American article, "Man Viewed as a Machine," Kemeny summarized lectures von Neumann had given just before Kemeny left Princeton. Kemeny framed the question of these lectures, "What could a machine do as well as or better than a man?" The conclusion in 1955 was that computers calculate faster than the human brain, may eventually match the human brain in memory capacity, but have a long way to go to exceed the compactness of the human brain or the complexity the human brain is capable of dealing with. Next, based on the work of the English logician Alan Turing, Kemeny argued that a universal machine can be designed. That universal machine would need a simple code designed for it that would describe any simple machine humans could devise. Then the universal machine could do anything every simple machine could do by converting the descriptions of the simple machines into programs for its own operation. It occurred to Kemeny that "a normal human being is like the universal machine. Given enough time he can learn to do anything." Kemeny carried this understanding with him throughout his career of encouraging universal teaching of computer programming.
In the summer of 1953, while a consultant at the Rand Corporation, Kemeny had a chance to use the JOHNNIAC, a copy of von Neumann's Princeton computer. He had great fun, he wrote, "learning to program a computer, even though the language used at that time was designed for machines and not for human beings" (Kemeny 1972, p. 7).
Kemeny joined the faculty of Dartmouth College in 1953 to teach mathematics and philosophy. For six years after he got there, Dartmouth had no computer. Kemeny could, however, commute 135 miles each way to use the computer at MIT in Cambridge, Mass. He did and therefore witnessed the coming, in 1957, of the Fortran programming language. Kemeny welcomed the language because it made much more sense to him to teach a machine a language than to force every human to learn the machine's own language. "All of a sudden access to computers by thousands of users became not only possible but reasonable" (Kemeny 1972, p. 8).
Dartmouth acquired its first computer in 1959, a Royal McBee LGP-30. Kemeny facilitated the use of the LGP-30 by undergraduate students. The ingenuity and creativeness of some of the students who had been given hands-on experience amazed the Dartmouth faculty. Kemeny and Thomas Kurtz, also of the Dartmouth Mathematics Department, were thus encouraged to "set in motion the then revolutionary concept of making computers as freely available to college students as library books" (Slater 1987, p. 22). The aim was to make accessible to all students the wonderful research environment that computers could provide.
The work of Kemeny and Kurtz in the early 1960s took two directions. Influenced by the work of J.C.R. Licklider and John McCarthy at MIT, Kemeny understood that a time-sharing system would make possible the universal access they aimed for. A team of the two faculty members and a group of undergraduate research assistants developed a prototype system. It allowed multiple users short spurts of access to the central computer from remote terminals in such a way that each user enjoyed the illusion that he was the sole user. This Dartmouth Time-Sharing System (DTSS) became operational in the fall of 1964. The value of a time-sharing system is that it ended the hardship of batch processing, which often required hours or even days of waiting between runs of a program while it was being developed and debugged. Time-sharing utilizes the great speed of computers compared to humans to greatly enhance the efficiency of computing from the point of view of the human users.
Today's packet switching networks (for example, the Internet) owe a great deal to the development of this time-sharing system, conceptually and technically. But earlier, DTSS almost got derailed. Kemeny had worked closely with General Electric during the time DTSS was being worked on. In 1966, GE and Dartmouth agreed to work on a joint development of the time-sharing operating system. However, GE's commercial purposes conflicted with Dartmouth's educational purposes. The story is told that GE tried to "stop the Dartmouth experiment" and the development of the time-sharing system called Phase I. (See Nelson 1974, p. 45.) But Kemeny and Kurtz, determined not to let DTSS disappear, encouraged the development of DTSS Phase II by 1969.
In addition to time-sharing, Kemeny and Kurtz realized that a new computer language was needed that could be easily learned and was accessible to typical college students. Kemeny noted, "We at Dartmouth envisaged the possibility of millions of people writing their own computer programs" (Kemeny 1972, p. 30). They designed their language with plain English and high school algebra-like commands so that the lay user could learn a very few commands and then be able to write interesting programs. Kemeny started to work on a draft version in September 1963. The result was BASIC, Beginners All-Purpose Symbolic Instruction Code. The first BASIC program ran on May 1, 1964, at 4:00 a.m. Kemeny and Kurtz made an effort to get as many students as possible using BASIC, and they were available to hear about problems and bugs and to come up with bug fixes. Kemeny and Kurtz wanted BASIC to be in the public domain; Dartmouth copyrighted BASIC but made it available without charge.
The careful work of Kemeny and Kurtz to make an easy-to-learn but powerful computer language bore tremendous fruit. After its introduction at Dartmouth in 1964, BASIC spread, as did DTSS, to other campuses and government and military situations. BASIC made personal computers possible. Beginning in 1975 with the success of Bill Gates and Paul Allen to write an interpreter for a subset of BASIC commands for the Altair computer, one form or another of BASIC spread to and accelerated the personal computer revolution.
For a while the great appeal of personal computers and their falling costs and general availability eclipsed Kemeny and Kurtz' seminal work on DTSS and the original BASIC. By the late 1980s, 10 to 12 million school children had learned BASIC, more people than speak, for example, Norwegian. The personal computer helped "distribute" computing, which Kemeny thought was crucial to the progress of society. But it also diminished in importance the centralized computing power and the interconnectivity of users that time-sharing made possible. Only recently, with the spread of computer networks, is the value of both developments being realized. Now the power of personal computer workstations, instead of dumb terminals, coupled with the connectivity and remote resource availability, is making possible the human-computer and human-human interfacing that Kemeny predicted.
From 1971 to 1980, Kemeny was the thirteenth president of Dartmouth College, presiding over (including other things) the transition there to coeducation. He continued his efforts to support a crucial role for computers in education but was unable to be a major contributor to developments like the personal computer and the various versions of BASIC. In 1979, Kemeny served as the chair of President Carter's Commission on the Accident at Three Mile Island. Kemeny "very much regretted" that the commission did not recommend a temporary halt on construction permits for nuclear reactors. The investigation had found that the government regulators were too lax in their regulation. The commission concluded, "the evidence suggests that the NRC (Nuclear Regulatory Commission) has sometimes erred on the side of the industry's convenience rather than carrying out its primary mission of insuring safety" and that the industry took inadequate safety precautions and failed to respond to known unsafe conditions (The Report of the President's Commission on the Accident at Three Mile Island, pp. 43, 51, 188).
After Kemeny stepped down from the presidency of Dartmouth and chair of the Three Mile Island Accident Commission, he took stock of the use of computers, especially in education. He was furious and frustrated by the slow progress of education in computer programming. Between 1983 and 1985, Kemeny and Kurtz went back to work and produced a portable and more powerful version of their original BASIC. They called it True BASIC and it is still marketed today with the intention of introducing "students to the very important art of computer programming and analytic thinking."
Kemeny had a very broad vision of the role computers would play in society. He foresaw a man-machine symbiosis that would help both to evolve rapidly. In the early 1970s he predicted that within 20 years there would be a national computer network with terminals in millions of homes, so every home would be a mini-university. He also predicted there would be a National Automated Reference Library, a national personalized computer-delivered news service, and, especially, greatly enhanced education via time-sharing and simple programming languages. Kemeny worked hard to implement his visions and felt by the late 1980s great disappointment in the slow progress. He died just as the great computer networking structures, which have developed in some large measure because of his pioneering work and vision, have begun to fulfill more of his expectations, but also just as a fight is being waged by those who want to commercialize these networking structures and those who want to keep them in the public domain.
Kemeny recognized that the social problems that have yet to be solved are immense. He wrote, "While computers alone cannot solve the problems of society, these problems are too complex to be solved without highly sophisticated use of computers" (Kemeny 1972, p. 80). He believed it is imperative that computers be freely available. "Only if we manage to bring up a computer-educated generation will society have modern computers fully available to solve its serious problems" (Kemeny 1972). He saw the computer revolution as a possible asset for society but felt "it is a major mistake to make plans for the solution of social problems on the assumption that society will in the future be organized in exactly the same way as today. For the first time in human history we have an opportunity for significant social planning. We cannot afford to waste it" (Kemeny 1972, p. 143).
John Kemeny was part of many of the seminal events of the computer revolution. He made major contributions to its foundation and he thought deeply into this revolution. His death was untimely but he has left the value of his work to help us take on the challenges that confront the progress to which he contributed.

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#773 2020-08-15 00:18:52
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
739) Margaret Eloise Knight
Margaret E. Knight, (born Feb. 14, 1838, York, Maine, U.S.—died Oct. 12, 1914, Framingham, Mass.), prolific American inventor of machines and mechanisms for a variety of industrial and everyday purposes.
Knight demonstrated a knack for tools and invention from an early age, and she was said to have contrived a safety device for controlling shuttles in powered textile looms when she was 12 years old. In 1868, at which time she was living in Springfield, Massachusetts, she invented an attachment for paper-bag-folding machines that allowed the production of square-bottomed bags. After working to improve her invention in Boston, she patented it in 1870. She later received patents for a dress and skirt shield (1883), a clasp for robes (1884), and a spit (1885). Later still she received six patents over a span of years for machines used in the manufacturing of shoes.
Other of Knight’s inventions included a numbering machine and a window frame and sash, both patented in 1894, and several devices relating to rotary engines, patented between 1902 and 1915. Although she was not the first woman to receive a patent, she was one of the most productive of female inventors, having some 27 patents to her credit. She failed to profit much from her work, however. When Knight died she was honoured in a local obituary as a “woman Edison.”

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#774 2020-08-17 00:39:07
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
740) Jean Baptiste Perrin
Jean Baptiste Perrin was born in Lille, September 30, 1870, where he was educated at the École Normal Supérieure, becoming an assistant in physics during 1894-1897, when he began his researches on cathode rays and X-rays. He received the degree of “docteur ès sciences” in 1897 for a thesis on cathode and Röntgen rays and was appointed, in the same year, to a readership in physical chemistry at the Sorbonne, University of Paris. He became Professor here in 1910; a post which he held till 1940, when the Germans invaded his country.
His earliest work was on the nature of cathode rays, and their nature was proved by him to be that of negatively charged particles. He also studied the effect of the action of X-rays on the conductivity of gases. In addition, he worked on fluorescence, the disintegration of radium, and the emission and transmission of sound. The work for which he is best known is the study of colloids and, in particular, the so-called Brownian movement. His results in this field were able to confirm Einstein’s theoretical studies in which it was shown that colloidal particles should obey the gas laws, and hence to calculate Avogadro’s number N, the number of molecules per grammolecule of a gas. The value thus calculated agreed excellently with other values obtained by entirely different methods in connection with other phenomena, such as that found by him as a result of his study of the sedimentation equilibrium in suspensions containing microscopic gamboge particles of uniform size. In this way the discontinuity of matter was proved by him beyond doubt: an achievement rewarded with the 1926 Nobel Prize.
Perrin was the author of many books and scientific papers. His book Les Atomes, published in 1913, sold 30,000 copies up to 1936. His principal papers were: “Rayons cathodiques et rayons X” (Cathode rays and X-rays), Ann. Phys., 1897; Les Principes (The principles), Gauthier-Villars, 1901; “Electrisation de contact” (Contact electrificaton), J. Chim. Phys., 1904-1905; “Réalité moléculaire” (Molecular reality), Ann. Phys., 1909; “Matière et Lumière” (Matter and light), Ann. Phys., 1919; “Lumière et Reaction chimique” (Light and chemical reaction), Conseil Solvay de Chimie, 1925.
Many honours were conferred on him for his scientific work; the Joule Prize of the Royal Society in 1896, the Vallauri Prize of Bologna in 1912 and, in 1914, the La Caze Prize of the Paris Academy of Sciences.
He held honorary doctorates of the Universities of Brussels, Liege, Ghent, Calcutta, New York, Princeton, Manchester, and Oxford. He was twice appointed a member of the Solvay Committee at Brussels in 1911 and in 1921. He held memberships of the Royal Society (London) and of the Academies of Sciences of Belgium, Sweden, Turin, Prague, Rumania, and China. In 1923 he was elected to the French Academy of Sciences. He became a Commander of the Legion of Honour in 1926, and was also made Commander of the British Empire and of the Order of Leopold (Belgium).
Perrin was the creator of the Centre National de la Recherche Scientifique, an organization offering to most promising French scientists – whose scientific talents would otherwise be lost – a career outside the University. It was due to this institute that Frédéric Joliot could carry out his magnificent investigations. In addition to this, he founded the Palais de la Découverte (Palace of discovery); he was also responsible for the establishment of the Institut d’Astrophysique, in Paris, and for the construction of the large Observatoire de Haute Provence; without his prestige and his power of persuasion the Institut de Biologie Physico-Chimique would never have come into being.
Perrin was an officer in the engineer corps during the 1914-1918 War. When the Germans invaded his country in 1940 he escaped to the U.S.A., where he died on the 17th of April, 1942. After the War, in 1948, his remains were transferred to his fatherland by the battleship Jeanne d’Arc, and buried in the Panthéon.

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#775 2020-08-19 00:53:13
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,498
Re: crème de la crème
741) Royal Earl House
Royal Earl House (9 September 1814 – 25 February 1895) was the inventor of the first printing telegraph, which is now kept in the Smithsonian Institution. His nephew Henry Alonzo House is also a noted early American inventor.
Royal Earl House spent his childhood in Vermont experimenting, designing, and building, a habit which would earn him distinction as an adult. He once caught a toad, skinned it, placed a set of springs in the skin and made it hop. Around 1840, he went to Buffalo, New York to live with relatives and attend law school in that town. However, he read a work on electricity which so inspired him that he decided to give up law and study the science of electricity instead. He was also interested in mechanics, chemistry and magnetism.
By 1846, the Morse telegraph service was operational between Washington, DC, and New York. Royal Earl House patented his printing telegraph that same year. He linked two 28-key piano-style keyboards by wire. Each piano key represented a letter of the alphabet and when pressed caused the corresponding letter to print at the receiving end. A "shift" key gave each main key two optional values. A 56-character typewheel at the sending end was synchronised to coincide with a similar wheel at the receiving end. If the key corresponding to a particular character was pressed at the home station, it actuated the typewheel at the distant station just as the same character moved into the printing position, in a way similar to the daisy wheel printer. It was thus an example of a synchronous data transmission system. House's equipment could transmit around 40 instantly readable words per minute, but was difficult to manufacture in bulk. The printer could copy and print out up to 2,000 words per hour. This invention was first put in operation and exhibited at the Mechanics Institute in New York in 1844.
In 1886 and 1887, when the Royal E. House telegraph company was producing the printing telegraph, the Morse Telegraph company tried to enjoin (legally prevent) them from infringing on the Morse patents. Morse claimed the sole right of transmitting intelligence by electricity, utilizing the Morse code. The courts decided the House Company did not infringe the Morse patent, as the messages using the House system were all printed on a slip of paper, without the use of Morse Code.
Later the House Co. and the Morse Co. joined and formed the Great Western Telegraph Company.

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline