Math Is Fun Forum

sologuitar

Member

Registered: 2022-09-19

Posts: 467

Solve for x

A friend texted the following question to me.

Solve x^(2) = 2^(x) for x.

Any suggestions?

Jai Ganesh

Administrator

Registered: 2005-06-28

Posts: 48,402

Re: Solve for x

The equation

has two "obvious" solutions: x=2 and x=4. They are "obvious" because they are relatively easy to find by sheer guessing or by sketching the graphs of the two functions involved, and once guessed they are trivial to verify.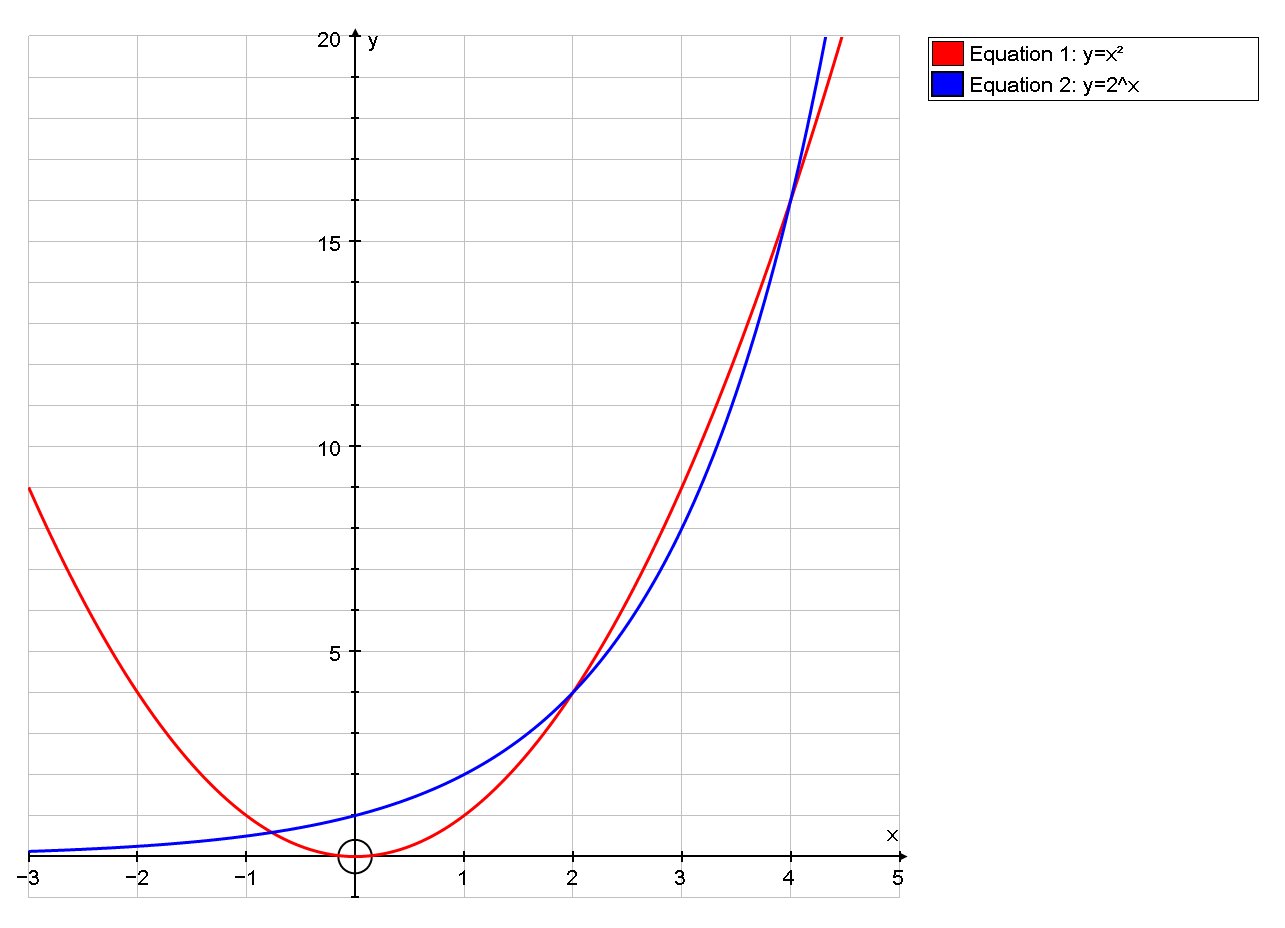

There is a third solution with x<0. That this solution exists is fairly obvious as well: just consider the general behavior of the two functions for negative values of x and you will see that they must intersect at least once - in fact it's not hard to see that they intersect exactly once in that region.

However, it is not possible (we believe!) to write down an explicit formula for that solution by using rational numbers, arithmetic operations, and the so-called Elementary Functions: exponentials, logarithms and trigonometric functions. It is possible to write down such an explicit expression using a decidedly less standard function, the Lambert W function, and that's pretty straightforward too.

Proving the negative assertion above is far from trivial, and in fact I don't think that such a proof is known. Just because the solution can be expressed by evaluating W at ln(2)/2 (and making a few other simple calculations) doesn't rule out the possibility that there is also another expression for that same solution using elementary functions evaluated at rational numbers.

There's a brilliant and readable paper by Tim Chow on this topic, called "What is a closed form number?" . I highly recommend it to anyone interested in gaining a deeper understanding of those questions. It is a little surprising that many people wouldn't hesitate to make the assertion I made above, about the negative solution being impossible to write down "in closed form", without having proof of that fact and often without even being able to express precisely what the claim is.

We can see there is one solution in the interval -1 < x < 0 and a second solution at what appears to be x = 2 and a third at what appears to be x = 4.  The two solution x = 2, 4  can easily be verified to be exact by substitution.

We can find the third solution numerically, using Newton-Rhapson method

Let

and using the Newton-Rhapson method we use the following iterative sequence.

And we conclude that the remaining solution is

to 4 dp.

---

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.

Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.

sologuitar

Member

Registered: 2022-09-19

Posts: 467

Re: Solve for x

The equation

has two "obvious" solutions: x=2 and x=4. They are "obvious" because they are relatively easy to find by sheer guessing or by sketching the graphs of the two functions involved, and once guessed they are trivial to verify.

https://useruploads.socratic.org/apnbo8bVTC6ioBCx7wzf_AutoGraph.jpg

There is a third solution with x<0. That this solution exists is fairly obvious as well: just consider the general behavior of the two functions for negative values of x and you will see that they must intersect at least once - in fact it's not hard to see that they intersect exactly once in that region.

However, it is not possible (we believe!) to write down an explicit formula for that solution by using rational numbers, arithmetic operations, and the so-called Elementary Functions: exponentials, logarithms and trigonometric functions. It is possible to write down such an explicit expression using a decidedly less standard function, the Lambert W function, and that's pretty straightforward too.

Proving the negative assertion above is far from trivial, and in fact I don't think that such a proof is known. Just because the solution can be expressed by evaluating W at ln(2)/2 (and making a few other simple calculations) doesn't rule out the possibility that there is also another expression for that same solution using elementary functions evaluated at rational numbers.

There's a brilliant and readable paper by Tim Chow on this topic, called "What is a closed form number?" . I highly recommend it to anyone interested in gaining a deeper understanding of those questions. It is a little surprising that many people wouldn't hesitate to make the assertion I made above, about the negative solution being impossible to write down "in closed form", without having proof of that fact and often without even being able to express precisely what the claim is.

We can see there is one solution in the interval -1 < x < 0 and a second solution at what appears to be x = 2 and a third at what appears to be x = 4.  The two solution x = 2, 4  can easily be verified to be exact by substitution.

We can find the third solution numerically, using Newton-Rhapson method

Let

and using the Newton-Rhapson method we use the following iterative sequence.

And we conclude that the remaining solution is

to 4 dp.

A very detailed reply. I thank you also for the photo.