Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2022-12-04 21:01:25
- mathdrop
- Member
- Registered: 2022-03-07
- Posts: 75
Egg formula
The longitudinal cut of an eggshell.
After everything below I hold the opinion, that it is an asymmetric ellipse.
First I digged into Wikipedia.
The cause of the shape of eggs according to an article, linked there, about Mary Caswell Stoddard and her team:
"It begins when an unfertilized egg cell is added to a globule of yolk, and sent down a bird’s oviduct... ...On its travels, it is fertilized by sperm, surrounded by white, and coated in two membranes. The membranes are pumped with fluid like a balloon being inflated, and finally surrounded by a shell. Counter-intuitively, it’s not the shell that matters most, but the membranes. If you dissolve the shell in acid, the naked egg will still retain its original shape."
They took the Baker-Formula and matched bird eggs with it (EggxTractor).
There are different construction methods.
The Wikipedia article also links a paper titled the mathematics of egg shape of Yutaka Nishiyama.
After explaining the Descartes approach, he goes on with the Cassini approach, which is more or less a shortcut of the former.
This could probably be read before taking on the Baker-Formula:
y=t(1+a)^(1/1+a)*(1−a)^(a/1+a)
t=(equatorial diameter)^(-1) ?
a=ln(heightright)/ln(heightleft)
There is another equation which
I struggle to let go of just yet.
It's the Blaschke one, I found on mathtinkering:
x^1.5-l^0.5x+y^2=0
y = ± (sqrt(x)*sqrt(sqrt(a)-sqrt(x)))
Since 2021 this formula of Narushin (see there for variable descriptions) was hyped:
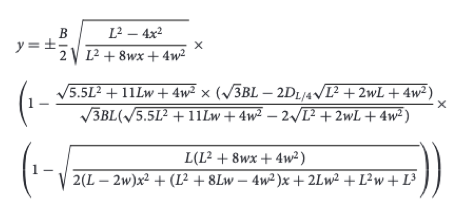
It already has this breadth value,
whch would have been left for me to calculate with the Baker formula
I will see how I like it.
So much for now.
Last edited by mathdrop (2023-02-20 02:35:39)
Offline
Pages: 1