Math Is Fun Forum

mathdrop

Member

Registered: 2022-03-07

Posts: 75

Superellipse

Superellipse on Wikipedia.

|x/a|^n+|y/b|^n=1 where n>=2
<=>
|y/b|^n=1-|x/a|^n
<=>
y/b=+/- (1-|x/a|^n)^(1/n)
<=>
y=+/- b*(1-|x/a|^n)^(1/n)  // absolute makes x<0 usable

a=semi-mayor axis (half-axis in x-direction)
b=semi-minor axis (half-axis in y-direction)

Of course, it has something of the hyperbola.

n=2 leaves the ellipse.
With n increasing from there, the shape converges to a rectangle.
The curvature is 0, where it crosses the axes.

Simplifying it to the supercircle,
which probably is an unsqueezed superelipse, so a=b:

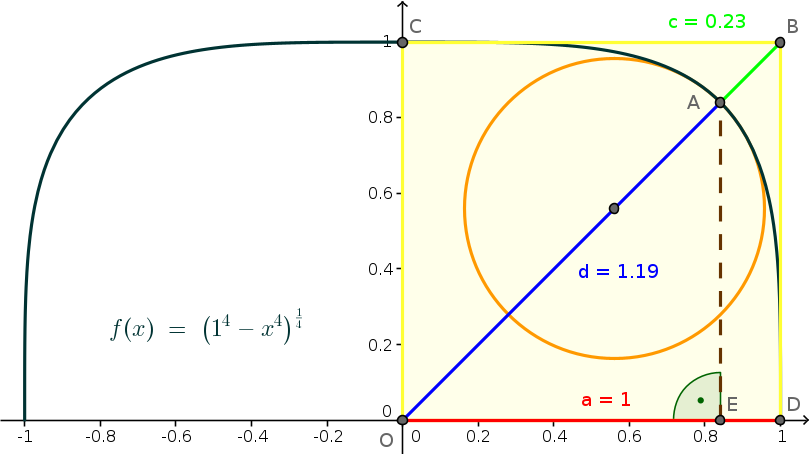
On Wikipedia, they call a supercircle where n=4 a squircle.
Without shifting and variables kept, they give x⁴+y⁴=a⁴ <=> y=+/- (a⁴-x⁴)^(1/4).
With n instead of 4, its the equivalent of a=b in the superelipse-formula at the top.
It seems also to work with a z-part: x^n+y^n+z^n=a^n <=> y=+/- (a^n-x^n-z^n)^(1/n)
Basically I refer to the 2D-Case where z=0, but will expand to 3D at times.

f(x,z,a,n)   = (a^n-x^n-z^n)^(1/n)
f'(x,z,a,n)  = -x^(n-1)*(a^n-x^n-z^n)^(1/n-1)  // slope
f''(x,z,a,n) = -(n-1)*x^(n-2)*(a^n-z^n)*(a^n-x^n-z^n)^(1/n-2)  // curvature use for elbowradius

some limit cases:
for n=2 the sqircle is a circle
for n=1 the sqircle is a square
for 0 < n < 1 the sqircle is a star

domain of squircle funtion f(x,z,a,n):  // xstart for slope-x-value newton aproxximation (functiondrawing)
a^n-x^n-z^n  // content of the root
a^n-z^n-x^n>=0  // which shouldn't be 0 or negative
a^n-z^n>=x^n
x<=(a^n-z^n)^(1/n)

Calculating the area and the perimeter is said to be complicated.
Regarding the area, there is however a shortcut using the Lemniscate Constant L~2.62205755429211981 .
So the area is A=L*sqrt(2)*a^2 . For now I will go with that.

A sidenote before I go deeper into the math:
While browsing the web I stumbled upon a post about a spherefactor-approach.

Below I mainly try to get the n out of the squircle functon.
Instead I throw in more common values out of the hyperbola properties.

c in f(x,a,c) is a counterpart for the semi major axis of a hyperbola
              (how far the curve is pulled into an rectangular edge).

r in f(x,a,r) is the radius in the elbow of a hyperbola
              (where the highest curvature is).

For the later an n which is described by r and a=r_min,
would probably have to be approximated.
I tried it with the newton procedure, which covered many cases.

The properties I come by may also be interresting for them selves
or handy for other calculations.

For getting the maximum radius (origin to rounded edge)
I'm intersecting the squircle with a line of slope=1:
f(x,a,n)=f(x,z=0,a,n)=(a^n-x^n)^(1/n)  // n=4: black line in the graph
g(x)=x  // straight 45° ascending line through origin
f(x)=g(x)
solve((a^n - x^n)^(1/n)=x,x)
The computer has not wanted to solve it with n,
but when I tried it with different numbers for n, it took the nth root,
so I've put n there.
x=a/2^(1/n)  // simplest positive non-imaginary solution out of 5, n=4: brown line in the graph
y=x since symmetry
a:=r_min  // red distance in the graph
d:=r_max  // blue distance in the graph
r_max=a/2^(1/n)*sqrt(2)=2^(1/2-1/n)*a

diagonal=r_min*sqrt(2)  // blue plus green line in the graph
c:=diagonal-r_max  // green line in the graph

c=a*sqrt(2)-a/2^(1/n)*sqrt(2)
=(a-a/2^(1/n))*sqrt(2)=sqrt(2)*(1-2^(-1/n))*a
<=>
a=(2^(1/n-1/2)*c)/(2^(1/n)-1) and 2^(1/n)!=1
<=>
n=-(i*log(2))/(2*π*c_1-i*log((sqrt(2)*a)/(sqrt(2)*a-c)))
  and sqrt(2) a!=c and a!=0 and log((sqrt(2)*a)/(sqrt(2)*a-c))+2*i*π*c_1!=0 and c_1 element Z
=log(4)/(2*log(a/(sqrt(2)*a-c))+4*i*π*c_1+log(2))  // variables real

Again without imaginaries:
c=sqrt(2)*(1-2^(-1/n))*a      |/sqrt(2)*a
<=>
c/(sqrt(2)*a)=1-2^(-1/n)      |-1
<=>
(c/(sqrt(2)*a))-1=-2^(-1/n)   |*(-1)
<=>
2^(-1/n)=1-(2^(-1/2)*c/a)     |^(-1)
<=>
2^(1/n)=1/(1-(2^(-1/2)*c/a))  |log, 1/(1-(2^(-1/2)*c/a))=(sqrt(2)*a)/(sqrt(2)*a-c)
<=>
1/n=log((sqrt(2)*a)/(sqrt(2)*a-c))/log(2)  |^(-1)
<=>
n=log(2)/log((sqrt(2)*a)/(sqrt(2)*a-c))

c'=d/dn=-(a*2^(1/2-1/n)*log(2))/n^2  // for newton approximation
f(x,c,n)=(((2^(1/n-1/2)*c)/(2^(1/n)-1))^n-x^n)^(1/n)
        =(2^(1-n/2)*((2^(1/n)-1)/c)^(-n)-x^n)^(1/n)  // variables positive
f(x,a,c)=(a^(-(2*i*log(2))/(-2*i*log(a/(sqrt(2)*a-c))+4*π*c_1-i*log(2)))-x^(-(2*i*log(2))/(-2*i*log(a/(sqrt(2)*a-c))+4*π*c_1-i*log(2))))^(log(a/(sqrt(2)*a-c))/log(2)+(2*i*π*c_1)/log(2))*sqrt(a^(-(2*i*log(2))/(-2*i*log(a/(sqrt(2)*a-c))+4*π*c_1-i*log(2)))*x^(-(2*i*log(2))/(-2*i*log(a/(sqrt(2)*a-c))+4*π*c_1-i*log(2)))*(x^((2*i*log(2))/(-2*i*log(a/(sqrt(2)*a-c))+4*π*c_1-i*log(2)))-a^((2*i*log(2))/(-2*i*log(a/(sqrt(2)*a-c))+4*π*c_1-i*log(2)))))
         and -2*i*log(a/(sqrt(2)*a-c))+4*π*c_1-i*log(2)!=0
Without imaginaries:
f(x,a,c)=(a^log(2)/log((sqrt(2)*a)/(sqrt(2)*a-c))-x^log(2)/log((sqrt(2)*a)/(sqrt(2)*a-c)))^(1/log(2)/log((sqrt(2)*a)/(sqrt(2)*a-c)))
        =((a^log(2)-x^log(2))/log(c/(sqrt(2)*a-c)+1))^(1/(log(2)*log(c/(sqrt(2)*a-c)+1)))   // variables positive

Check:
f(x,c,n)=0  // x-intersect=r_min
(2^(1-n/2)*((2^(1/n)-1)/c)^(-n)-x^n)^(1/n)=0
x=(2^(1-n/2)*((2^(1/n)-1)/c)^(-n))^(1/n)
=(2^(1/n-1/2)*c)/(2^(1/n)-1) and 2^(1/n)!=1  // variables positive
=r_min=a (see above)

Elbow-radius:
r=1/curvature
r=1/f''(a/2^(1/n))
=-(a^(-n)*(a*2^(-1/n))^(2-n)*(a^n-(a*2^(-1/n))^n)^(2-1/n))/(n-1)
=(2^(-1-1/n)*a)/(1-n)  // variables positive

For n between ]1,infinity[, this gives half the negative radius.
Why half and why negative ?

Correction by manipulating the numerator (1 -> -2):
r=-2/f''(a/2^(1/n))
=-2*(2^(-1-1/n)*a)/(1-n)
=(2^(-1/n)*a)/(n-1)
<=>
a=2^(1/n)*(n-1)*r and Re(n)<1
<=>
a/r=2^(1/n)*(n-1)
<=>
n=not solvable
r'=d/dn=-(a*2^(-1/n)*(n^2-n*log(2)+log(2)))/((n-1)^2*n^2)  // for newton approximation
f(x,r,n)=((2^(1/n)*(n-1)*r)^n-x^n)^(1/n)
        =(2*(n-1)^n*r^n-x^n)^(1/n)  // variables positive
f(x,a,r)=not findable

f(x,r,n)=0  // x-intersect=r_min
((2^(1/n)*(n-1)*r)^n-x^n)^(1/n)=0
x=((2^(1/n)*(n-1)*r)^n)^(1/n)
=2^(1/n)*n*r-2^(1/n)*r=2^(1/n)*(n-1)*r  // variables positive
=r_min=a (see above)

checking it with some limit cases:

for n=2 the sqircle is a circle
r=(2^(-1/n)*a)/(n-1)
r=(2^(-1/2)*a)/(2-1)=a/sqrt(2)
<=>
a=sqrt(2)*r  // shouldn't a=r ?

what would that further mean ?:
if r > a/sqrt(2) then its edgy
if r = a/sqrt(2) then its a circle
if r < a/sqrt(2) then its a squirce

for n=1 the sqircle is a square
r=(2^(-1/n)*a)/(n-1)
r=(2^(-1/1)*a)/(1-1)=division by zero, complex infinity
this result seems to be satisfying,
cause a square does have no radius.

for 0 < n < 1 the sqircle is a star

Last edited by mathdrop (2023-02-20 03:18:36)