Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2023-11-20 17:04:57
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 52,733
Specific Gravity
Specific Gravity
Gist
The specific gravity of an object is the density of that object divided by the density of water. The density of water is 1,000 kilograms per meter cubed. For instance, the density of gold is 19,300 kilograms per meter cubed. So the specific gravity of gold is 19.3.
Summary
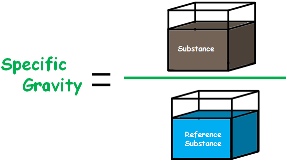
Specific gravity is the ratio of the density of a substance to that of a standard substance.
The usual standard of comparison for solids and liquids is water at 4 °C (39.2 °F), which has a density of 1.0 kg per litre (62.4 pounds per cubic foot). Gases are commonly compared with dry air, which has a density of 1.29 grams per litre (1.29 ounces per cubic foot) under so-called standard conditions (0 °C and a pressure of 1 standard atmosphere). For example, liquid mercury has a density of 13.6 kg per litre; therefore, its specific gravity is 13.6. The gas carbon dioxide, which has a density of 1.976 grams per litre under standard conditions, has a specific gravity of 1.53 (= 1.976/1.29). Because it is the ratio of two quantities that have the same dimensions (mass per unit volume), specific gravity has no dimension.
Buoyancy (the ability of an object to float in water or air) is intimately related to specific gravity. If a substance has specific gravity less than that of a fluid, it will float on that fluid: helium-filled balloons will rise in air, oil will form a slick on water, and lead will float on mercury. The specific gravity of a substance is characteristic; it is the same for different samples of a substance (if pure, the same in composition, and free from cavities or inclusions) and is used to help identify unknown substances. Specific gravity has many other applications: gemologists use it to distinguish similar gems; chemists, to check on the progress of reactions and the concentration of solutions; and auto mechanics, to test battery fluid and antifreeze.
Specific gravity is the basis of methods used throughout history to concentrate ores. Panning, jigging, shaking, spiral separation, and heavy-medium separation are among the methods that depend on differences in specific gravity to obtain concentrated ore. Specific gravity is highest in rocks rich in iron, magnesium oxide, and the heavy metals and lowest in those rich in alkalies, silica, and water.
The ease with which specific gravity can be precisely determined leads to its widespread use in chemical science and technology; for example, determination of the specific gravity is part of the routine characterization of a new liquid compound. The specific gravity of most organic compounds containing only carbon, hydrogen, and oxygen is less than one. Among the devices used to measure specific gravity are the Westphal balance, the pycnometer, and the hydrometer.
Details
Relative density, sometimes called specific gravity, is a dimensionless quantity defined as the ratio of the density (mass of a unit volume) of a substance to the density of a given reference material. Specific gravity for liquids is nearly always measured with respect to water at its densest (at 4 °C or 39.2 °F); for gases, the reference is air at room temperature (20 °C or 68 °F). The term "relative density" (often abbreviated r.d. or RD) is often preferred in scientific usage, whereas the term "specific gravity" is deprecated.
If a substance's relative density is less than 1 then it is less dense than the reference; if greater than 1 then it is denser than the reference. If the relative density is exactly 1 then the densities are equal; that is, equal volumes of the two substances have the same mass. If the reference material is water, then a substance with a relative density (or specific gravity) less than 1 will float in water. For example, an ice cube, with a relative density of about 0.91, will float. A substance with a relative density greater than 1 will sink.
Temperature and pressure must be specified for both the sample and the reference. Pressure is nearly always 1 atm (101.325 kPa). Where it is not, it is more usual to specify the density directly. Temperatures for both sample and reference vary from industry to industry. In British brewing practice, the specific gravity, as specified above, is multiplied by 1000. Specific gravity is commonly used in industry as a simple means of obtaining information about the concentration of solutions of various materials such as brines, must weight (syrups, juices, honeys, brewers wort, must, etc.) and acids.
Uses
Relative density can also help to quantify the buoyancy of a substance in a fluid or gas, or determine the density of an unknown substance from the known density of another. Relative density is often used by geologists and mineralogists to help determine the mineral content of a rock or other sample. Gemologists use it as an aid in the identification of gemstones. Water is preferred as the reference because measurements are then easy to carry out in the field.
As the principal use of relative density measurements in industry is determination of the concentrations of substances in aqueous solutions and these are found in tables of RD vs concentration it is extremely important that the analyst enter the table with the correct form of relative density. For example, in the brewing industry, the Plato table, which lists sucrose concentration by mass against true RD, were originally (20 °C/4 °C) that is based on measurements of the density of sucrose solutions made at laboratory temperature (20 °C) but referenced to the density of water at 4 °C which is very close to the temperature at which water has its maximum density of ρ(H2O) equal to 0.999972 g/{cm}^3 (or 62.43 lb·ft^{-3}). The ASBC table in use today in North America, while it is derived from the original Plato table is for apparent relative density measurements at (20 °C/20 °C) on the IPTS-68 scale where the density of water is 0.9982071 g/{cm}^3. In the sugar, soft drink, honey, fruit juice and related industries sucrose concentration by mass is taken from this work which uses SG (17.5 °C/17.5 °C). As a final example, the British RD units are based on reference and sample temperatures of 60 °F and are thus (15.56 °C/15.56 °C).
Measurement
Relative density can be calculated directly by measuring the density of a sample and dividing it by the (known) density of the reference substance. The density of the sample is simply its mass divided by its volume. Although mass is easy to measure, the volume of an irregularly shaped sample can be more difficult to ascertain. One method is to put the sample in a water-filled graduated cylinder and read off how much water it displaces. Alternatively the container can be filled to the brim, the sample immersed, and the volume of overflow measured. The surface tension of the water may keep a significant amount of water from overflowing, which is especially problematic for small samples. For this reason it is desirable to use a water container with as small a mouth as possible.
Digital density meters
Hydrostatic Pressure-based Instruments: This technology relies upon Pascal's Principle which states that the pressure difference between two points within a vertical column of fluid is dependent upon the vertical distance between the two points, the density of the fluid and the gravitational force. This technology is often used for tank gaging applications as a convenient means of liquid level and density measure.
Vibrating Element Transducers: This type of instrument requires a vibrating element to be placed in contact with the fluid of interest. The resonant frequency of the element is measured and is related to the density of the fluid by a characterization that is dependent upon the design of the element. In modern laboratories precise measurements of relative density are made using oscillating U-tube meters. These are capable of measurement to 5 to 6 places beyond the decimal point and are used in the brewing, distilling, pharmaceutical, petroleum and other industries. The instruments measure the actual mass of fluid contained in a fixed volume at temperatures between 0 and 80 °C but as they are microprocessor based can calculate apparent or true relative density and contain tables relating these to the strengths of common acids, sugar solutions, etc.
Ultrasonic Transducer: Ultrasonic waves are passed from a source, through the fluid of interest, and into a detector which measures the acoustic spectroscopy of the waves. Fluid properties such as density and viscosity can be inferred from the spectrum.
Radiation-based Gauge: Radiation is passed from a source, through the fluid of interest, and into a scintillation detector, or counter. As the fluid density increases, the detected radiation "counts" will decrease. The source is typically the radioactive isotope caesium-137, with a half-life of about 30 years. A key advantage for this technology is that the instrument is not required to be in contact with the fluid—typically the source and detector are mounted on the outside of tanks or piping.
Buoyant Force Transducer: the buoyancy force produced by a float in a homogeneous liquid is equal to the weight of the liquid that is displaced by the float. Since buoyancy force is linear with respect to the density of the liquid within which the float is submerged, the measure of the buoyancy force yields a measure of the density of the liquid. One commercially available unit claims the instrument is capable of measuring relative density with an accuracy of ± 0.005 RD units. The submersible probe head contains a mathematically characterized spring-float system. When the head is immersed vertically in the liquid, the float moves vertically and the position of the float controls the position of a permanent magnet whose displacement is sensed by a concentric array of Hall-effect linear displacement sensors. The output signals of the sensors are mixed in a dedicated electronics module that provides a single output voltage whose magnitude is a direct linear measure of the quantity to be measured.
It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
Pages: 1