Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2007-01-13 07:11:07
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
cool pool physics
Hey guys, I havent taken any physics courses yet, (though Im going to be soon enough.) But I was thinking about the physics of colliding billiard balls for a practice program and how the math works. I read a rule that when a ball in motion contacts a still ball, their deflected paths always differ by 90 degrees. That gave me some clues. I spent a night puzzling over how the vectors might behave, particularly why two balls that collide with equal speeds bounce back instead of the forces canceling eachother out.
Anyway, I think I did it and I built a simulation with gamemaker to test my math. You can download it here if you want to try it out. (go to http://www.freewebs.com/mikau16/games/pool.exe if that link doesn't work) Its about 1.2 mb. Just point where you want to shoot, and hold in the mouse for a bit to give it some power. Its rough and unpolished right now, the collisions are a little goofy at high speeds and there are bugs everywhere, but it demonstrates the physics pretty well I think.
Now Ill talk about how I worked out the math if you want to hear about it.
From what I read the directions always differ by 90 degrees when you hit a still ball, now you know the still ball is going to move directly away from the contact point, thus the ball that struck it is going to move in a path tangent to the contact point. That gave me an idea. You can always describe an objects speed by two perpendicular components, such as vertical and horizontal speed. But it seemed when the ball in motion struck the other ball, the component of the speed that was moving directly towards the contact point was transferred to the other ball, while the component of speed perpendicular to that, remained. This would explain why the other ball would move straight away from the contact point while the ball that struck it would move at a 90 degree angle.
Therefore the task would be to find these two components of speed. I did this by rotating the coordinate axis so that the y axis was paralell to the line through the centerpoint of the two balls. Now we get the force at which the balls strike echother directly, and the horizontal components that dont effect it.
So the last question was, what happens when both balls are in motion? Well I realized when one ball strikes another, the component of speed moving directly towards it is completely transferred to the other ball, so that component is still and empty, add anything to it and it will start moving again. Thats when I realized what happens. When two balls in motion strike eachother, the components of speed heading directly towards eachother are swapped. They each give the other the entirety of that direct impact speed component but keep the (perpendicular) component remaining.
So the task became simple. When two balls contact, rotate the coordinate axis till the y axis is paralell to the line through their centerpoints. Then find the vertical and horizontal components of their speed in this new, rotated coordinate plane, then swap their vertical components, leaving the horizontals as they are, then rotate the coordinate axis back to get them back in their proper form. Its easiest to do this using polarform of course. And thats all!
Here are some pics to help describe what I mean. 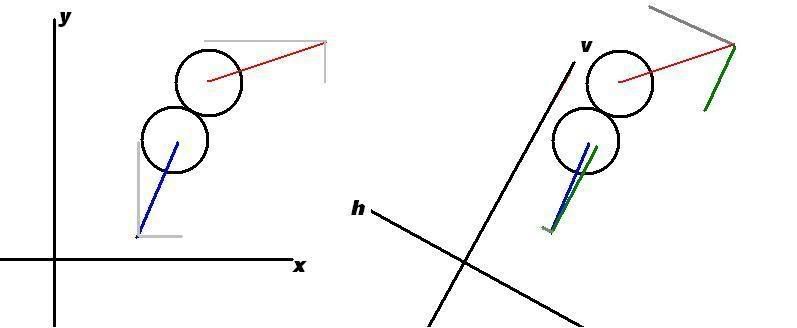
This shows the rotated coordinate axis and the original and new components of the speed.
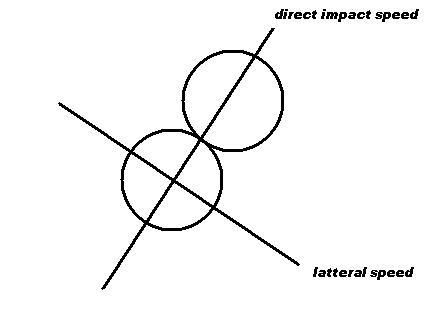
This pic shows what I mean by direct component of speed. The speed needs to be described as horizontal and vertical components on this coordinate axis. The speed and direction are the same theyre just described in relation to something else. When two balls collide, the direct components of speed are swapped while the latteral components are unchanged.
Anyways, I hope my explanation is clear enough. Just reinventing the wheel as usual. If any portion of my physics is inaccurate or illogical please comment. But if I did get something wrong, I think my game test shows I was pretty close, whatever I did. Give it a try!
Last edited by mikau (2007-01-13 08:07:54)
A logarithm is just a misspelled algorithm.
Offline
#2 2007-01-13 08:46:59
- Ricky
- Moderator

- Registered: 2005-12-04
- Posts: 3,791
Re: cool pool physics
The general solution, that is, collisions between spheres traveling in 3d (i.e. floating in space), is not too hard to understand. Would you like me to post the algorithm, or discuss first?
"In the real world, this would be a problem. But in mathematics, we can just define a place where this problem doesn't exist. So we'll go ahead and do that now..."
Offline
#3 2007-01-13 08:47:50
- Ricky
- Moderator

- Registered: 2005-12-04
- Posts: 3,791
Re: cool pool physics
Mikau, your link seems to be broken.
"In the real world, this would be a problem. But in mathematics, we can just define a place where this problem doesn't exist. So we'll go ahead and do that now..."
Offline
#4 2007-01-13 08:54:55
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: cool pool physics
I think you've got the physics of it pretty much right. There are probably a few extra complications that you haven't considered that would make the game more accurate, but it's certainly a good model.
One example of said complications would be the coefficient of elasticity, or how much the balls bounce off each other. If the balls were magnetic, for example, then once they struck each other then they would never separate again and they'd combine their momenta to determine the velocity of the resulting mass. The coefficient of elasticity there would be 0. I think in your model, you've made the coefficient of elasticity be 1, but that's pretty close to what snooker balls do anyway, so that's OK.
One thing I like about this game is that you can potentially do really powerful shots. So you can get lots of balls bouncing off multiple cushions and because they're moving so much, it becomes likely that quite a few of them will go in. And then if anyone was watching,you'd be able to comment on how incredibly skilful you were at judging that shot perfectly, even though it was a complete fluke. ![]()
Another game that uses the same physics is here. The concept is a bit different, because you don't control the balls yourself. You just need to move your mouse around to avoid them. But the physics of them is very good indeed, and it's a very fun game. The best I've survived is about 2 seconds after the 10th ball gets introduced.
Edit: To Ricky, the link doesn't work, but if you copy and paste the url just after it into your browser then it should work. Which is odd because the two urls are exactly the same. Maybe the forum has a security thing that prevents directly linking to .exe files.
Why did the vector cross the road?
It wanted to be normal.
Offline
#5 2007-01-13 09:59:55
- Patrick
- Real Member

- Registered: 2006-02-24
- Posts: 1,005
Re: cool pool physics
Cool game ![]() The whole thing with directions seems very realistic..
The whole thing with directions seems very realistic..
Support MathsIsFun.com by clicking on the banners.
What music do I listen to? Clicky click
Offline
#6 2007-01-13 10:59:40
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: cool pool physics
Thanks guys! Yeah for some reason that direct link isn't working even though it references the exact same adress. Peculiar...
I also drew all the sprites. :-) Except for the table texture which i got off google. Now I want to work a bit on the cushion physics. Right now the cushions use simplified physics but on a real table they are angled at the pockets. You usually bounce off the corner of the cushion when you make a corner pocket. So I need to be able to create cushions of different shapes where the balls rebound off them correctly. So thats the next step.
The last step is to add a bit of english to the game. That oughta be tricky as well.
Ricky, I hadn't thought about it but I assume it works the same way, only the direct only there are three componants (for the 3 dimensions). One direct componant of force and two indirect. But I would like to hear a bit about it.
Last edited by mikau (2007-01-13 11:37:56)
A logarithm is just a misspelled algorithm.
Offline
#7 2007-01-13 22:47:13
- Patrick
- Real Member

- Registered: 2006-02-24
- Posts: 1,005
Re: cool pool physics
haha, didn't notice 'till now.. The right-click thing is fun ![]()
Support MathsIsFun.com by clicking on the banners.
What music do I listen to? Clicky click
Offline
#8 2007-01-13 23:09:23
- luca-deltodesco
- Member

- Registered: 2006-05-05
- Posts: 1,470
Re: cool pool physics
im not quite sure how you are doing this from your explanation, the way i do it is like this:
suppose you have two balls:
the first ball is defined by its position a and its velocity v and its mass m
the second ball is defined by its position b and its velocity q and its mass M
now supposing the balls are just touching, are colliding, i would calculate the vector between their centers
and divide this by the sum of the radii, so that its normalised.i would then calculuate
if x is less then 0, i would set it to 0
if y is more than 0, i would set it to 0
the resulting velocities of the two balls would then be given by
if you take the sum of the momentums before and after, they would be exactly the same this way, the force applied to the other ball, is in the direction of the normal, with magnitude dictated by the cosine of the angle between the normal of impact and the velocity and the magnitude of the velocity.
the reason for capping x to be >= 0 and y to <= 0, is so that in the case, when you might have one ball moving foward, and another ball hit it from behind, it would stop any momentum from the ball infront being transferred to the one behind.
http://denvish.net/ulf/1168772893_snowfall.php
(im actually using this as a preloader for a game im making, as witnessed by the 'play' button and percentage that has been loaded underneath ![]() )
)
in this simulation i added some dampeners aswell so the balls would slow down.
one thing i find quite fun about this, is that the time progression is based on the time elapse of the frame, and i calculate the next collision mathematicly, resolve the collisions, and in the frame, keep progressing through collisions till the time step has been completed, so that if you hold the close window button, and pause the flash movie, when you let go, itll run through the entire simulation through the amount of time you kept it paused ![]()
Last edited by luca-deltodesco (2007-01-13 23:16:49)
The Beginning Of All Things To End.
The End Of All Things To Come.
Offline
#9 2007-01-13 23:18:20
- Patrick
- Real Member

- Registered: 2006-02-24
- Posts: 1,005
Re: cool pool physics
luca - if you click and hold one of the keys, the ball will eventually disappear
Support MathsIsFun.com by clicking on the banners.
What music do I listen to? Clicky click
Offline
#10 2007-01-13 23:31:12
- luca-deltodesco
- Member

- Registered: 2006-05-05
- Posts: 1,470
Re: cool pool physics
what? ive never seen a ball dissapear, the only time a ball will ever dissapear in this simulation, is in the event that two collisions occur at the EXACT same time, because it will only process one of them, and the other will then be implanted in a wall or something, and i dont test for this, so it will then just move through it, but thats not very common.
The Beginning Of All Things To End.
The End Of All Things To Come.
Offline
#11 2007-01-14 00:11:00
- Patrick
- Real Member

- Registered: 2006-02-24
- Posts: 1,005
Re: cool pool physics
what? ive never seen a ball dissapear, the only time a ball will ever dissapear in this simulation, is in the event that two collisions occur at the EXACT same time, because it will only process one of them, and the other will then be implanted in a wall or something, and i dont test for this, so it will then just move through it, but thats not very common.
I've done it 5 times now, so obviously it can't be the only time a ball will ever disappear.
Support MathsIsFun.com by clicking on the banners.
What music do I listen to? Clicky click
Offline
#12 2007-01-14 01:28:50
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: cool pool physics
I've never seen a ball disappear either, but maybe Patrick was playing with it for longer than me. Nice game though. I especially like how you've made the ball distort when it's moving fast.
Why did the vector cross the road?
It wanted to be normal.
Offline
#13 2007-01-14 07:21:51
- Patrick
- Real Member

- Registered: 2006-02-24
- Posts: 1,005
Re: cool pool physics
it can disappear after a matter of seconds if you don't get hit by balls.. just force it into a corner and let it hit the walls untill it suddently goes through the wall.
Support MathsIsFun.com by clicking on the banners.
What music do I listen to? Clicky click
Offline
#14 2007-01-14 07:55:22
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: cool pool physics
Ooh, true enough. It takes a bit of a while, because the ball's bounciness makes it hard to keep in the corner, but once it's there it does slip through the wall. Also, if you click play to get the ball back, you can't control it anymore.
Edit: Actually, that second thing happens even if the first one doesn't. If you click play to reset the ball positions, you lose control.
Not that either of those matter, of course. We only found those bugs because we weren't playing with it properly.
Why did the vector cross the road?
It wanted to be normal.
Offline
#15 2007-01-14 18:44:43
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: cool pool physics
haha, didn't notice 'till now.. The right-click thing is fun
What the HECK? Lol. Oops! I had no idea that was there! Thats a vestage of some previous test. Not supposed to be there! x_x hehe! oh well. Glitches are fun to play with.
A logarithm is just a misspelled algorithm.
Offline
#16 2007-01-15 08:31:01
- Patrick
- Real Member

- Registered: 2006-02-24
- Posts: 1,005
Re: cool pool physics
haha, didn't notice 'till now.. The right-click thing is fun
What the HECK? Lol. Oops! I had no idea that was there! Thats a vestage of some previous test. Not supposed to be there! x_x hehe! oh well. Glitches are fun to play with.
Haha, okay ![]()
Support MathsIsFun.com by clicking on the banners.
What music do I listen to? Clicky click
Offline
#17 2007-01-15 08:40:39
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: cool pool physics
Once, due to a typo, when one ball struck another, the other ball was given more momentum then the first and took off with greater speed. With lots of balls on the table it makes some funny stuff happened. I pocketed all but 3 balls on the break!
Some glitches actually give you ideas.
A logarithm is just a misspelled algorithm.
Offline
Pages: 1