Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#651 2007-05-22 11:58:07
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: 0.9999....(recurring) = 1?
Plus, assuming his homepage is up to date, Sekky doesn't even have a degree himself anyway. ![]()
Why did the vector cross the road?
It wanted to be normal.
Offline
#652 2007-05-23 01:11:16
- Anthony.R.Brown
- Banned
- Registered: 2006-11-16
- Posts: 516
Re: 0.9999....(recurring) = 1?
Quote:" Hey Anthony, can I see your degree? "
A.R.B
my degree! is always lower than other's but then I just like being Cool..............................
Offline
#653 2007-05-23 01:45:36
- luca-deltodesco
- Member

- Registered: 2006-05-05
- Posts: 1,470
Re: 0.9999....(recurring) = 1?
do you even know what a degree is lol?
The Beginning Of All Things To End.
The End Of All Things To Come.
Offline
#654 2007-05-23 01:55:57
- Sekky
- Member
- Registered: 2007-01-12
- Posts: 181
Re: 0.9999....(recurring) = 1?
my degree! is always lower than other's but then I just like being Cool..............................
Oh, becuase that makes so much sense.
Offline
#655 2007-05-23 01:58:17
- Anthony.R.Brown
- Banned
- Registered: 2006-11-16
- Posts: 516
Re: 0.9999....(recurring) = 1?
Quote" Oh, becuase that makes so much sense. "
A.R.B
Fools paradise!
Offline
#656 2007-05-24 21:38:45
- Daniel123
- Member

- Registered: 2007-05-23
- Posts: 663
Re: 0.9999....(recurring) = 1?
What would 0.999999...9² be? Wouldn't it have a 1 and an 8 in it? so it couldnt equal 1, but 1² = 1?
Offline
#657 2007-05-24 23:48:18
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: 0.9999....(recurring) = 1?
Good question. I think I can explain it like this:
The following pattern was found in another topic.
9² = 81
99² = 9801
999² = 998001
9999² = 99980001
You can put decimal points in front of each of those to change the pattern like this:
0.9² = 0.81
0.99² = 0.9801
0.999² = 0.998001
0.9999² = 0.99980001
This pattern continues to give the general case of 0.(x 9's)² = 0.([x-1] 9's) 8 ([x-1] 0's) 1.
Taking this to the limit as x goes to ∞, we get 0.999...² = 0.999...8000...1
But as there are an infinite amount of 9s in that number (and thus, no last 9), we never actually reach the 8.
Therefore 0.999...8000...1 = 0.999... and so 0.999...² = 0.999...
Why did the vector cross the road?
It wanted to be normal.
Offline
#658 2007-05-24 23:52:30
- Daniel123
- Member

- Registered: 2007-05-23
- Posts: 663
Re: 0.9999....(recurring) = 1?
Aah i never thought of it like that, but even if we never actually reach the 8, we still know it's there don't we? so couldn't we argue that 0.999...² could not posible be 1 as a result of this 8, therefore 0.999... could not be 1 either, because 1² = 1.
Offline
#659 2007-05-25 00:13:55
- Maelwys
- Member
- Registered: 2007-02-02
- Posts: 161
Re: 0.9999....(recurring) = 1?
Aah i never thought of it like that, but even if we never actually reach the 8, we still know it's there don't we? so couldn't we argue that 0.999...² could not posible be 1 as a result of this 8, therefore 0.999... could not be 1 either, because 1² = 1.
"...we still know it's there..."
It's where?
It's in the "infinity+1"th position away from the 0? Well, since such a position doesn't exist within our definition of infinity, then there's nowhere for the 8 to be, meaning that it isn't anywhere. So as stated above, 0.999...² = 0.999...
And since the only case we know of in which x²=x, x>0 is where x=1, this could also be seen as another (rather long, roundabout) proof that 0.999... = 1.
;-)
Offline
#660 2007-05-25 00:21:33
- Anthony.R.Brown
- Banned
- Registered: 2006-11-16
- Posts: 516
Re: 0.9999....(recurring) = 1?
To Maelwys
Quote:" And since the only case we know of in which x²=x, x>0 is where x=1, this could also be seen as another (rather long, roundabout) proof that 0.999... = 1.
;-) "
A.R.B
Exactly! pure precision accuracy is what we are after! as with Infinite 1.111...x 0.9 = 0.999....
Offline
#661 2007-05-25 02:22:40
- Ricky
- Moderator

- Registered: 2005-12-04
- Posts: 3,791
Re: 0.9999....(recurring) = 1?
It's in the "infinity+1"th position away from the 0? Well, since such a position doesn't exist within our definition of infinity, then there's nowhere for the 8 to be, meaning that it isn't anywhere. So as stated above, 0.999...² = 0.999...
Be careful with throwing the word "infinity" around. There are many types of infinity. If you say "countable infinity" instead, your statement becomes absolutely correct.
What do decimals actually mean? Say you have a number:
This number is:
So for example, 0.485 is 0 + 4/10 + 8/100 + 5/1000.
It should be obvious that:
And so if you do wish to talk about the "infinitith" position, you would be adding on 0, and not changing the number. But since this sequence is countable, there is no such thing as an infinith position. Every position has a finite index. The 100th decimal is 100 digits away from the decimal point. The 105815908280824 decimal is 105815908280824 digits away from the decimal point. There are an infinite amount of digits, but each and every one of them has a finite distance from the decimal point.
"In the real world, this would be a problem. But in mathematics, we can just define a place where this problem doesn't exist. So we'll go ahead and do that now..."
Offline
#662 2007-05-25 10:21:29
- Daniel123
- Member

- Registered: 2007-05-23
- Posts: 663
Re: 0.9999....(recurring) = 1?
Ive never really thought of this before... what is the number before 0.999... ?
Offline
#663 2007-05-25 10:24:47
- luca-deltodesco
- Member

- Registered: 2006-05-05
- Posts: 1,470
Re: 0.9999....(recurring) = 1?
theres no such thing as 'the number before' there is not one, same way that there is not a number before 2 or 3, the reals are dense, so there is no countability, unlike integers where you have clearly defined 1,2,3,4, the number before 4 is 3, the number before 2 is 1 etc.
The Beginning Of All Things To End.
The End Of All Things To Come.
Offline
#664 2007-05-25 16:20:14
- Ricky
- Moderator

- Registered: 2005-12-04
- Posts: 3,791
Re: 0.9999....(recurring) = 1?
the reals are dense, so there is no countability
Density does not imply uncountability. But they are both dense and uncountable.
"In the real world, this would be a problem. But in mathematics, we can just define a place where this problem doesn't exist. So we'll go ahead and do that now..."
Offline
#665 2007-05-25 18:45:59
- luca-deltodesco
- Member

- Registered: 2006-05-05
- Posts: 1,470
Re: 0.9999....(recurring) = 1?
really? i cant think of any examples where density doesnt give uncountability
The Beginning Of All Things To End.
The End Of All Things To Come.
Offline
#666 2007-05-25 23:33:52
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: 0.9999....(recurring) = 1?
Rationals are one example. It seems a bit counterintuitive though - the rationals are countable, and yet because they're dense you can't count them. ![]()
Why did the vector cross the road?
It wanted to be normal.
Offline
#667 2007-05-26 04:54:34
- Ricky
- Moderator

- Registered: 2005-12-04
- Posts: 3,791
Re: 0.9999....(recurring) = 1?
Sure you can mathysperson, just not from lowest to highest:
1/1, 1/2, 2/1, 1/3, 3/1, 2/3, 3/2, 1/4, 4/1, ...
"In the real world, this would be a problem. But in mathematics, we can just define a place where this problem doesn't exist. So we'll go ahead and do that now..."
Offline
#668 2007-05-26 05:40:51
- luca-deltodesco
- Member

- Registered: 2006-05-05
- Posts: 1,470
Re: 0.9999....(recurring) = 1?
but thats not counting, your'e going up and down the number scale.
The Beginning Of All Things To End.
The End Of All Things To Come.
Offline
#669 2007-05-26 05:59:35
- Sekky
- Member
- Registered: 2007-01-12
- Posts: 181
Re: 0.9999....(recurring) = 1?
but thats not counting, your'e going up and down the number scale.
That's counting, all you're doing is sequentially arranging the numbers. Essentially the fact that he's even suggested a sequence (which happens to be the accepted canonical sequence, although I can't see anyone doing it another way) implies that you can count them, because you can actively determine the next rational in sequence. You can't determine the next real in the same manner.
Offline
#670 2007-05-26 07:30:25
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: 0.9999....(recurring) = 1?
Ah, of course. I was forgetting that counting didn't necessarily need to be in order.
It has to be that way, because some countable sets aren't ordered anyway.
There are other sequences for counting the rationals, but the only ones I can think of are a bit messy.
For example, a way of showing that the rationals are countable is to say that they all take the form a/b*c, where a and b are natural, and abs(c) = 1.
Then you can map each rational number to a natural by 2^a x 3^b x 5^[(1-c)/2].
Lots of naturals don't get mapped to there, but that doesn't particularly matter.
The naturals *are* countable in order, and so you can put the subset of naturals that get mapped to in order, and then do the inverse of that to get another way of counting rationals.
Why did the vector cross the road?
It wanted to be normal.
Offline
#671 2007-05-26 08:10:23
- LQ
- Real Member
- Registered: 2006-12-04
- Posts: 1,285
Re: 0.9999....(recurring) = 1?
Isn't it simpler to put it like this:
1 - .999... = .000...
1 - .000... = .999...
(1 - .000...)^2 = 1^2 + .000...^2 - 2*1*.000... = 1 + .000... - 2*.000... = 1 - .000... = 1
Last edited by LQ (2007-05-26 16:49:02)
I see clearly now, the universe have the black dots, Thus I am on my way of inventing this remedy...
Offline
#672 2007-05-26 08:14:26
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: 0.9999....(recurring) = 1?
The first line makes use of the fact that 0.999... = 1, which is what we're trying to prove. Albeit in a long, convoluted way.
Why did the vector cross the road?
It wanted to be normal.
Offline
#673 2007-05-26 10:00:32
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: 0.9999....(recurring) = 1?
hey guys, I posted this in a 0.999... thread in the Euler Avenue forum, but it looks like this is more the official thread for this topic. So I'm moving it here.
What do you think of this proof?
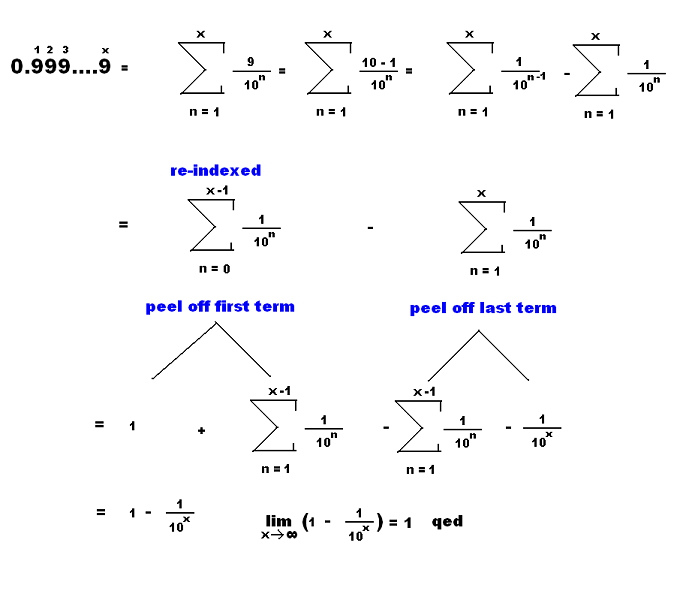
A logarithm is just a misspelled algorithm.
Offline
#674 2007-05-26 10:39:47
- Ricky
- Moderator

- Registered: 2005-12-04
- Posts: 3,791
Re: 0.9999....(recurring) = 1?
mikau, it's valid, but there are much easier ways to evaluate the sum, such as geometric series.
"In the real world, this would be a problem. But in mathematics, we can just define a place where this problem doesn't exist. So we'll go ahead and do that now..."
Offline
#675 2007-05-26 16:51:23
- LQ
- Real Member
- Registered: 2006-12-04
- Posts: 1,285
Re: 0.9999....(recurring) = 1?
The first line makes use of the fact that 0.999... = 1, which is what we're trying to prove. Albeit in a long, convoluted way.
Nope. that's how you write it.
I see clearly now, the universe have the black dots, Thus I am on my way of inventing this remedy...
Offline