Sticks!

JaneFairfax · 2008-05-20 03:45:59

I found this game on another forum. Ive been thinking on the solution for quite a while, but I believe Ive now solved it completely.

15 sticks are arranged in a Pascals triangle as follows:

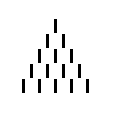
Two players take it in turn to remove sticks from the triangle. At least one stick must be removed by the player whose turn it is to play; if there are two or more adjacent sticks in the same row, the player may remove any number of them. Sticks in different rows do not count as adjacent. The player left with the last stick loses the game.

A typical game may proceed as follows:

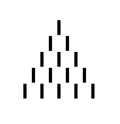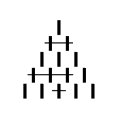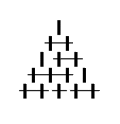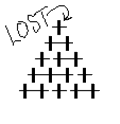
The question is: What move should the player going first make in order to force victory?

Well, after spending a long time over the puzzle, I can finally prove my claim that the opening move should be to remove one stick at either of the the extreme ends of the bottom row. To prove it, I shall have to establish a few theorems (scenarios).

Last edited by JaneFairfax (2008-05-20 03:52:19)

JaneFairfax · 2008-05-20 04:50:23

First we make a couple of definitions.

Definitions:
(i) A single is a single stick that is not adjacent to any other stick.

(ii) A pair is a set of two sticks that are adjacent to each other and to no other stick.

NB: The definitions imply that singles and pairs cannot be adjacent. Four adjacent sticks in a row do not count as two pairs or four singles.

A triplet (three adjacent sticks not adjacent to any other stick) and quadruplet (four adjacent sticks not adjacent to any other stick) can be similarly defined.

Scenario One (S1):
If there are an odd number of singles left, the person whose turn it is to move loses.

This is so intuitively obvious that a proof isnt really necessary. If you like, it can be proved by induction all the same.

Scenario Two (S2):
If there are two pairs left, the person whose turn it is to move loses.

NB: In all these scenarios, the person whose turn it is to move will lose. Lets call this player PT for short; similarly, call the other player PO.

Proof of S2: PT can either remove 1 stick or 2. If he removes 1 stick, PO removes 2 sticks, and vice versa. QED.

Scenario Three (S3):
If the sticks left are a single, a pair, and a triplet, the person whose turn it is to move loses.

Proof of S3:
(i) If PT removes the pair, PO removes the triplet, and vice versa, leaving the single for PT.

(ii) If PT removes one stick from the pair, PO removes two sticks from the triplet, and vice versa. This leaves 3 singles, and by S1 PT loses.

(ii) If PT removes the middle stick from the triplet, PO removes the pair. This also leaves 3 singles.

(iv) If PT removes one end stick from the triplet, PO removes the single, and vice versa. This leaves two pairs (S2).

QED.

Scenario Four (S4):
If there are two quadruplets left, the person whose turn it is to move loses.

Proof of S4:
(i) If PT removes one entire quadruplet, PO removes three sticks from the other quadruplet, and vice versa.

(ii) If PT removes the two middle sticks from one quadruplet, PO also removes three sticks from the other quadruplet. This will leave 3 singles (S1).

(iii) If PT removes two sticks including one at an extreme end of a quadruplet, PO does the same thing to the other quadruplet, leaving two pairs (S2).

(iv) If PT removes one extreme-end stick in one quadruplet, PO removes one of the two middle sticks in the oither quadruplet, and vice versa. This leaves S3.

QED.

Last edited by JaneFairfax (2008-05-20 23:34:52)

JaneFairfax · 2008-05-20 05:12:37

Scenario Five (S5):
If there are four pairs left, the person whose turn it is to move loses.

Proof of S5: As for S2, PT must start by removing 1 or 2 sticks. If PT removes a pair, PO removes another pair, leaving S2. If PT removes just one stick, PO removes one stick from a different pair. This leaves 2 pairs and 2 singles. If PT removes one of the singles, PO removes the other single leaving S2 for PT. If PT removes one stick from one of the pairs, PO removes the last remaining pair, while if PT removes a pair, PO removes one stick from the other pair in both cases leaving 3 singles (S1). QED.

Scenario Six (S6):
If any of the above scenarios are accompanied by an even number of singles, the person whose turn it is to move loses.

This is also fairly intuitively obvious, so a completely rigorous proof isnt necessary. I will just illustrate by an example. Suppose there are, say, two quadruplets and two singles left. This is essentially the same as the S4 game. If PT removes one of the singles at any time during the S4 game, PO will immediately remove the other single, thus forcing PT to resume the S4 game as if nothing had happened. On the other hand, if PT doesnt touch the singles until the S4 game is played out, then since PT will have lost the S4 game it will be POs turn to move when it comes to the last two sticks. Hence PT loses. The point is, that the evenness of the number of singles always enables PO to maintain parity in the tempo of the game.

Scenario Seven (S7):
If there are three pairs, a single and a triplet left, the person whose turn it is to move loses.

Proof of S7:
(i) If PT removes the single, PO removes one end stick from the triplet, and vice versa. S5 is left.

(ii) If PT removes the triplet or just the middle stick of the triplet, PO removes one stick from one of the pairs, and vice versa. The result is S6 (S2 + 2 or 4 singles).

(iii) If PT removes a pair, PO removes another pair, leaving S3.

QED.

Scenario Eight (S8):
If there are two pairs and two quadruplets left, the person whose turn it is to move loses.

Proof of S8:
(i) If PT removes one pair, PO removes the other pair, leaving S4. If PT removes one quadruplet or just the middle 2 sticks of one quadruplet, PO removes the whole of other quadruplet, leaving S2 or S2 + 2 singles.

(ii) If PT removes two sticks including one end stick from one quadruplet, PO does exactly the same thing to the other quadruplet, leaving S5.

(iii) If PT removes one stick from one pair, PO removes one stick from the other pair. If PT removes three sticks or one non-end stick from one quadruplet, PO does the same thing to the other quadrupet. All these should leave S6, in one guise or another.

(iv) If PT removes one end stick from one quadruplet, removing one non-end stick from the other quadruplet will leave S7.

QED.

Last edited by JaneFairfax (2008-05-20 06:00:29)

JaneFairfax · 2008-05-20 06:24:12

Well, you get the idea.

So, the game is between two players, and by getting the first move right, the first player can always force the second player into assuming the role of PT in a scenario like the ones Ive described. And I claim that the correct first move is to remove either the extreme-left or the extreme-right stick in the fifth row. After typing out the proofs of eight scenarios, I dont feel like doing the same thing for all the logical outcomes of the game itself. Can I leave you to convince yourself with your own proof?

mathsyperson · 2008-05-20 07:31:00

Nice work! One minor thing - you haven't addressed when PT removes 2 sticks from a triplet in S7. It doesn't affect your result though, because PO can remove a pair to be left with S6.

John E. Franklin · 2008-05-20 07:37:14

Hi J & m:
Looks like a fun game.
I learned a game like this in 1988, but it was just one row of sticks, and
I figured out how to win if I went first.
I haven't investigated your detailed work as mathsy has, however.
(I was thinking at first the rules were going to allow diagonal play as
well until I read you can't)

mathsyperson · 2008-05-20 07:49:17

Wow, diagonal play would make it considerably more interesting. There must still be a winning strategy for one of the players, but I'd hate to start analysing that game. Jane?

MathsIsFun · 2008-05-20 10:51:09

Amazing analysis, J.

BTW we could make a Flash version of it ... what would be the computer's strategy (easy/medium/hard) ?

JaneFairfax · 2008-05-20 12:20:13

Yes, a Flash game would be fun although the computer mustnt be unbeatable. How about just too levels: beginner, and advanced?

Incidentally, there are a few scenarios I didnt consider e.g. if there are two triplets, PT will lose. However, as you can see, the later scenarios tend to be built on the simpler ones and I think I have the simple ones covered. Some of the scenarios can even be generalized but since were only playing with 15 sticks, I thought there was no point in generalizing too much.

And I missed a minor detail in S7. Thanks Mathsy!

mathsyperson · 2008-05-20 22:39:33

I'd say the computer should be given a library of scenarios like the ones in Jane's posts. If it can make a move so that one of those scenarios is reached, it does that. Otherwise, it picks a move randomly.

The difference between easy, medium and hard would be the number of scenarios in the library. Also, perhaps the easier difficulties could have a small chance of "messing up" on each move.

Math Is Fun Forum

#1 2008-05-20 03:45:59

Sticks!

#2 2008-05-20 04:50:23

Re: Sticks!

#3 2008-05-20 05:12:37

Re: Sticks!

#4 2008-05-20 06:24:12

Re: Sticks!

#5 2008-05-20 07:31:00

Re: Sticks!

#6 2008-05-20 07:37:14

Re: Sticks!

#7 2008-05-20 07:49:17

Re: Sticks!

#8 2008-05-20 10:51:09

Re: Sticks!

#9 2008-05-20 12:20:13

Re: Sticks!

#10 2008-05-20 22:39:33

Re: Sticks!

Board footer