Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#1 Re: This is Cool » Miscellany » Today 00:06:36
2520) Fathometer
Gist
A fathometer is a specialized sonar-based instrument used to measure the depth of water (bathymetry) by calculating the time it takes for a sound wave to travel from the surface to the bottom and return as an echo. It is primarily used for navigation, mapping the seafloor, identifying fish, and checking ice thickness.
What is a fathometer used for measuring?
A fathometer is a device that measures the depth of water by measuring the time it takes for a sound wave to travel from the surface to the bottom and for its echo to be returned.
Summary
“A fathometer is a device that measures the depth of water by measuring the time it takes for a sound wave to travel from the surface to the bottom and for its echo to be returned.”
“Echo sounding or depth sounding is the use of sonar for ranging, normally to determine the depth of water (bathymetry). It involves transmitting acoustic waves into water and recording the time interval between emission and return of a pulse; the resulting time of flight, along with knowledge of the speed of sound in water, allows determining the distance between sonar and target. This information is then typically used for navigation purposes or in order to obtain depths for charting purposes.”
Had the fathometer, or echo sounder, been available, it might have changed maritime warfare during the First World War. The Fathometer, first offered for sale in 1923, uses sound waves to quickly and accurately determine water depth and detect underwater objects, like submarines. Before echo sounders, sailors dropped and retrieved weighted hand-held lines (lead lines) to estimate water depth. After the sinking of Titanic in 1912, Canadian engineer Reginald A. Fessenden wanted to improve underwater object detection and communications. An expert in wireless radio technology, Fessenden built an electromagnetic device, called the oscillator, which produced underwater sound waves. These waves bounced off objects and, by measuring the echoes produced by the returning waves, users could estimate the position of the object. Tests in 1914 proved the oscillator could not only detect icebergs, but also determine water depth. Fessenden urged war planners to use the oscillator as a submarine detector, but with his prickly personality, he was rebuffed. After the war, the Submarine Signal Company of Boston incorporated Fessenden’s oscillator technology in the fathometer, opening a new era of navigation, subsurface detection, and marine mapping.
Herbert Grove Dorsey (April 24, 1876 – 1961) was an American engineer, inventor and physicist. He was principal engineer of the United States Coast and Geodetic Survey Radio sonic Laboratory in the 1930s. He invented the first practical fathometer, a water depth measuring instrument for ships.
The depth of the ocean is calculated by knowing how fast sound travels in the water (approximately 1,500 meters per second). This method of seafloor mapping is called echo sounding. … Water depth is typically measured by echo sounders that transmit sound at 12 kilohertz (kHz).
Depth finder, also called echo sounder, device used on ships to determine the depth of water by measuring the time it takes a sound (sonic pulse) produced just below the water surface to return, or echo, from the bottom of the body of water. … sonar devices are used to measure the depth of sea.
Details
A fathometer is a device that measures the depth of water by measuring the time it takes for a sound wave to travel from the surface to the bottom and for its echo to be returned.
A Fathometer is used in ocean sounding when the depth of water is considerably deep and keeps a continuous and precise record of the depth of water under the boat or ship on which it is placed. It is an echo-sounding device in which water depths are determined by measuring the time it takes for vibrations produced by sound waves to travel from a location near the top of the water to the bottom and back. Depending on the kind of water being utilised, it is calibrated to read depth in line with the velocity of sound in that water. A fathometer may either visually represent the depth of the water or graphically indicate the depth of the water on a roll that is continually rotating and can produce a virtual profile of that water body. The fathometer meaning is derived from the word fathom. Fathom is a unit of water depth. Herbert Grove Dorsey invented and patented the first practical fathometer in 1928.
Working of fathometer
Fathometer working is quite simple and accurate compared to older methods of distance measuring of water bodies like the lead lines. A fathometer contains the following parts:
1. Transmitting and receiving oscillators ( for sending and receiving the sound waves )
2. Recorder unit ( for the recording of data)
3. Transmitter / Power unit. (power supply)
The distance between the signal’s leaving pulse and its return is calculated by multiplying half of the time between the signal’s outgoing pulse and its return by the sound speed in the water, roughly 1.5 kilometres per second. When using echo-sounding for precise applications such as hydrography, it is necessary to measure the sound speed, which is commonly accomplished by submerging a sound velocity probe into the water. Echo sounding is a special-purpose use of sonar that is used to find the bottom of any water bodies.
The Fessenden Fathometer was one of the earliest commercial echo- machines, and it made use of the Fessenden oscillator to create sound waves. Submarine Signal Company fitted this for the first time aboard the M&M liner S.S. Berkshire in 1924.
The fathometer is more accurate because it obtains a sounding that is exactly vertical. The vessel’s speed causes it to diverge significantly from the vertical. The precision of 7.5 cm is possible in ports and harbours when the water is at normal levels and conditions. When there is a strong current, and the weather is not conducive to taking soundings with the lead line, a fathometer may be employed (an Old device to measure the depth of water). The fathometer has a higher sensitivity than the lead line.
Uses of fathometer
1. Fathometer echo sounding is a technique that is often employed in fishing. Variations in elevation are often associated with areas where fish gather. In addition, schools of fish will be recorded. Fishfinder is an echo-sounding instrument, similar to a fathometer, that is used by both recreational and commercial fishermen to locate fish and other marine life.
2. This fathometer is installed on almost all ships and submarines in order to get an idea of the depth of water bodies and the morphology of rocks and seabeds in the area surrounding the ships and submarines.
3. It may also be used to measure the rise and fall of the tides in areas where the water is shallow.
4. The lead line is also one of the techniques for measuring the depth of water bodies, but it takes time and cannot be used in bad weather, so it has limited applications. The fathometer, on the other hand, can be used in bad weather and provides a more accurate result in a shorter period of time, making it more useful.
5. The same technique as the fathometer is used to send out sonic pulses in order to identify underwater things.
6. When it comes to submarines, a fathometer is quite important. Along with shoal water protection, other peacetime applications include identifying fish, assessing the thickness of ice in Arctic areas, and mapping the ocean’s surface.
7. A fathometer, also known as a Sonic depth finder, may be used to create a profile of the ocean bottom by recording thousands of soundings each hour over a long period of time. The use of echo sounders in oceanography and survey work to locate underwater pinnacles and shoals is common practice among hydrographers.
Conclusion
A fathometer is a device that uses echo sounding to measure the depth of the ocean or any other water bodies. Fathom is the unit for measuring the depth of any water body. A fathometer is more useful compared to conventional instruments to measure the depth because it can be used in bad weather and is more accurate with only an error of ± 7 cm. A fathometer is also used to locate the iceberg below the sea surface and schools of fish.
Additional Information
A Fathometer is used in ocean sounding where the depth of water is too much, and to make a continuous and accurate record of the depth of water below the boat or ship at which it is installed. It is an echo-sounding instrument in which water depths are obtained be determining the time required for the sound waves to travel from a point near the surface of the water to the bottom and back. It is adjusted to read depth on accordance with the velocity of sound in the type of water in which it is being used. A fathometer may indicate the depth visually or indicate graphically on a roll which continuously goes on revolving and provide a
virtual profile of the lake or sea.
What are the components of echo sounding instrument?
The main parts of an echo-sounding apparatus are:
1. Transmitting and receiving oscillators.
2. Recorder unit.
3. Transmitter / Power unit.
It consists in recording the interval of time between the emission of a sound impulse direct to the bottom of the sea and the reception of the wave or echo, reflected from the bottom. If the speed of sound in that water is v and the time interval between the transmitter and receiver is t, the depth h is given by
h = ½ vt
…
Due to the small distance between the receiver and the transmitter, a slight correction is necessary in shallow waters. The error between the true depth and the recorded depth can be calculated very easily by simple geometry. If the error is plotted against the recorded depth, the true depth can be easily known. The recording of the sounding is produced by the action of a small current passing through chemically impregnated paper from a rotating stylus to an anode plate. The stylus is fixed at one end of a radial arm which revolves at constant speed. The stylus makes a record on the paper at the instants when the sound impulse is transmitted and when the echo returns to the receiver.
Advantage of echo-sounding
Echo-sounding has the following advantages over the older method of lead line and rod:
1. It is more accurate as a truly vertical sounding is obtained. The speed of the vessel does deviate it appreciably from the vertical. Under normal water conditions, in ports and harbors an accuracy of 7.5 cm may be obtained.
2. It can be used when a strong current is running and when the weather is unsuitable for the soundings to be taken with the lead line.
3. It is more sensitive than the lead line.
4. A record of the depth is plotted immediately and provides a continuous record of the bottom as the vessel moves forward.
5. The speed of sounding and plotting is increased.
6. The error due to estimation of water level in a choppy sea is reduced owing to the instability of the boat.
7. Rock underlying softer material is recorded and this valuable information is obtained more cheaply than would be the case where sub-marine borings are taken.
Making the soundings
If the depth is less than 25 m, the soundings can be taken when the boat is in motion. In the case of soundings with rod the leadsman stands in the bow and plunges the rod at a forward angle, depending on the speed o the boat, such that the rod is vertical when the boat reaches the point at which soundings is being recorded. The rod should be read very quickly. The nature of the bottom should also be recorded at intervals in the note-book.
If the sounding is taken with a lead, the leadsman stands in the bow of the boat and casts the lead forward at such a distances that the line will become vertical and will reach the bottom at a point where sounding is required. The lead is withdrawn from the water after the reading is taken. If the depth is great, the lead is not withdrawn from the water, but is lifted between the soundings.

#2 Re: Dark Discussions at Cafe Infinity » crème de la crème » Today 00:06:15
2457) Fritz Albert Lipmann
Gist:
Work
In 1937 Hans Krebs presented a complete picture of an important part of metabolism—the citric acid cycle. In this process, which has several steps, nutrients are converted to other molecules with a large amount of chemical energy. An important piece of the process was still missing—a substance that along with a protein forms an enzyme that facilitates an important step. In 1946 the substance was discovered by Fritz Lipmann, who described its role plays and gave it the name coenzyme A.
Summary
Fritz Albert Lipmann (born June 12, 1899, Königsberg, Ger. [now Kaliningrad, Russia]—died July 24, 1986, Poughkeepsie, N.Y., U.S.) was a German-born American biochemist, who received (with Sir Hans Krebs) the 1953 Nobel Prize for Physiology or Medicine for the discovery of coenzyme A, an important catalytic substance involved in the cellular conversion of food into energy.
Lipmann earned an M.D. degree (1924) and a Ph.D. degree (1927) from the University of Berlin. He conducted research in the laboratory of the biochemist Otto Meyerhof at the University of Heidelberg (1927–30) and then did research at the Biological Institute of the Carlsberg Foundation (Carlsbergfondets Biologiske Institut), Copenhagen (1932–39), and at the Cornell Medical School, New York City (1939–41).
At Massachusetts General Hospital, Boston (1941–57), where he directed the biochemistry research department, and as professor of biological chemistry at the Harvard Medical School (1949–57), Lipmann found a catalytically active, heat-stable factor in pigeon liver extracts. He subsequently isolated (1947), named, and determined the molecular structure (1953) of this factor, coenzyme A (or CoA), which is now known to be bound to acetic acid as the end product of sugar and fat breakdown in the absence of oxygen. Coenzyme A is one of the most important substances involved in cellular metabolism; it helps in the conversion of amino acids, steroids, fatty acids, and hemoglobins into energy.
Lipmann taught or conducted research at the Rockefeller Institute, now Rockefeller University, New York City, from 1957 until his death.
Details
Fritz Albert Lipmann (June 12, 1899 – July 24, 1986) was a German-American biochemist and a co-discoverer in 1945 of coenzyme A. For this, together with other research on coenzyme A, he was awarded the Nobel Prize in Physiology or Medicine in 1953 (shared with Hans Adolf Krebs).
Early life and education
Lipmann was born in Königsberg, Germany, to a Jewish family. His parents were Gertrud (Lachmanski) and Leopold Lipmann, an attorney.
Lipmann studied medicine at the University of Königsberg, Berlin, and Munich, graduating in Berlin in 1924. He returned to Königsberg to study chemistry under Professor Hans Meerwein. In 1926 he joined Otto Meyerhof at the Kaiser Wilhelm Institute for Biology, Dahlem, Berlin, for his doctoral thesis. After that he followed Meyerhof to Heidelberg to the Kaiser Wilhelm Institute for Medical Research.
Career
From 1939 on, Lipmann lived and worked in the United States. He was a Research Associate in the Department of Biochemistry, Cornell University Medical College, New York from 1939 to 1941. He joined the research staff of the Massachusetts General Hospital in Boston in 1941, first as a Research Associate in the Department of Surgery, then heading his own group in the Biochemical Research Laboratory of the hospital. From 1949 to 1957 he was professor of biological chemistry at Harvard Medical School. From 1957 onwards, he taught and conducted research at Rockefeller University, New York City.
In 1953, Lipmann received one half of the Nobel Prize in Physiology and Medicine "for his discovery of co-enzyme A and its importance for intermediary metabolism." The other half of the award was won by Hans Adolf Krebs. Lipmann was awarded the National Medal of Science in 1966. He would try to dive further into his discovery by finding a variant of co-enzyme A, now known as Pantethine. He was an elected member of the American Academy of Arts and Sciences, the United States National Academy of Sciences, and the American Philosophical Society.
Lipmann introduced the specific squiggle designation (~) to indicate high energy-rich phosphate in energy-rich biomolecules like ATP in his essay "Metabolic Generation and Utilization of Phosphate Bond Energy." Of his work, he said "that in the field of biosynthesis we have a rare example of progress leading to simplification."
Personal life
In 1931, Lipmann married Elfreda M. Hall. They had one son.[2] Lipmann died in New York in 1986.The photo shows Mary Soames, not Elfreda Hall Lipmann[10] His widow died in 2008 at the age of 101.

#3 Jokes » Nut Jokes - II » Today 00:05:45
- Jai Ganesh
- Replies: 0
Q: What is a squirrels favorite ballet?
A; The nutcracker.
* * *
Q: Why did the squirrel take apart the classic car?
A: To get down to the nuts and bolts.
* * *
Q: Why couldn't the squirrel eat the macadamia nut?
A: It was one tough nut to crack.
* * *
Q: What do you get when you cross a spider and a squirrel?
A: A bug that will run up your leg and eat your nuts.
* * *
Q: What did the Psychologist say to the Squirrel with multiple personalities?
A: You're one tough nut to crack!
* * *
#4 Dark Discussions at Cafe Infinity » Comedy Quotes - I » Today 00:04:53
- Jai Ganesh
- Replies: 0
Comedy Quotes - I
1. Life is a tragedy when seen in close-up, but a comedy in long-shot. - Charlie Chaplin
2. Socialism is a fraud, a comedy, a phantom, a blackmail. - Benito Mussolini
3. Even actresses that you really admire, like Reese Witherspoon, you think, 'Another romantic comedy?' You see her in something like 'Walk the Line' and think, 'God, you're so great!' And then you think, 'Why is she doing these stupid romantic comedies?' But of course, it's for money and status. - Gwyneth Paltrow
4. I know nothing about love and romance, so I prefer to stick to just comedy. - Sandra Bullock
5. Comedy just pokes at problems, rarely confronts them squarely. Drama is like a plate of meat and potatoes, comedy is rather the dessert, a bit like meringue. - Woody Allen
6. Brad will tell you. He puts a movie on, I'm asleep in 10 minutes. I have no patience. But the kids love action movies with comedy, Jackie Chan and all that. - Angelina Jolie
7. People know me. I'm not going to produce any cartwheels out there. I'm not going to belong on Comedy Central. I'll always be a tennis player, not a celebrity. - Pete Sampras
8. When you make a drama, you spend all day beating a guy to death with a hammer, or what have you. Or, you have to take a bite out of somebody's face. On the other hand, with a comedy, you yell at Billy Crystal for an hour, and you go home. - Robert De Niro.
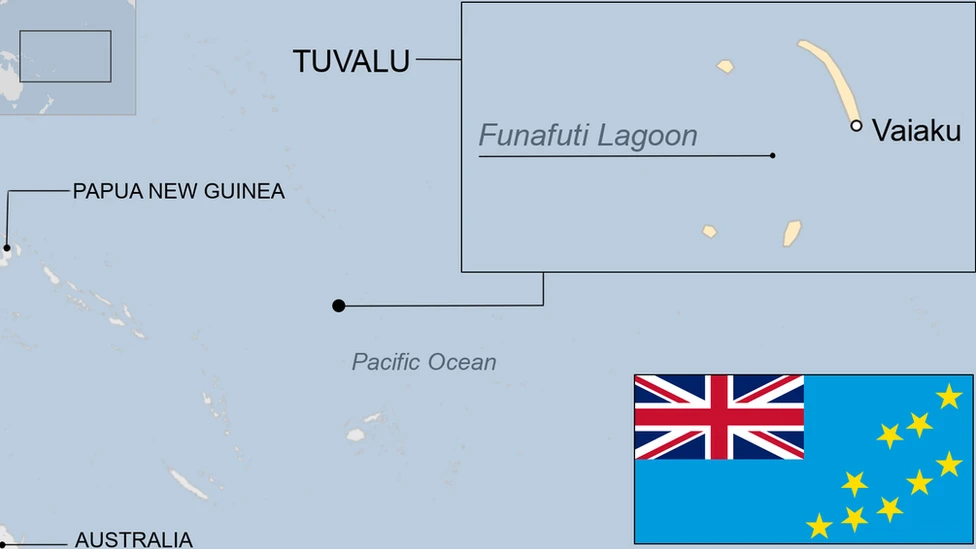
#5 This is Cool » Tuvalu » Yesterday 17:56:29
- Jai Ganesh
- Replies: 0
Tuvalu
Gist
Tuvalu is a small Polynesian island nation in the South Pacific, situated midway between Australia and Hawaii. Comprising nine low-lying coral atolls with a population of roughly 11,000, it faces severe threats from rising sea levels. Funafuti is the capital, and the country is known for its strong community culture and vulnerability to climate change.
Nobody visits Tuvalu much because it's incredibly remote, hard to get to with limited, expensive flights (from Fiji), lacks major tourist infrastructure, and faces an existential threat from climate change and rising sea levels, though it's open for visitors seeking a unique, off-the-beaten-path experience. Its tiny size, basic amenities, and high travel costs deter mass tourism, despite its natural beauty and Polynesian culture.
Summary
Tuvalu is a group of nine tiny islands in the South Pacific which won independence from the United Kingdom in 1978.
Five of the islands are coral atolls, the other four consist of land rising from the sea bed.
Formerly known as the Ellice Islands, all are low-lying, with no point on Tuvalu being higher than 4.5m above sea level. Local politicians have campaigned against climate change, arguing that it could see the islands swamped by rising sea levels.
Life on the islands is simple and often harsh. There are no streams or rivers, so the collection of rain is essential.
Coconut palms cover most of the islands, and copra - dried coconut kernel - is practically the only export commodity. Increasing salination of the soil threatens traditional subsistence farming.
Tuvalu has shown ingenuity by exploiting another source of income. It has sold its .tv internet suffix to a Californian company for several million dollars a year in continuing revenue. The company sells the suffix on to television broadcasters.
Fats
Capital: Funafuti
Population: 11,500
Area: 26 sq km
Languages: Tuvaluan, English
Life expectancy: 62 years (men) 67 years (women).
Details
Tuvalu is an island country in the Polynesian sub-region of Oceania in the Pacific Ocean, about midway between Hawaii and Australia. It lies east-northeast of the Santa Cruz Islands (which belong to the Solomon Islands), northeast of Vanuatu, southeast of Nauru, south of Kiribati, west of Tokelau, northwest of Samoa and Wallis and Futuna, and north of Fiji.
Tuvalu is composed of three reef islands and six atolls spread out between the latitude of 5° and 10° south and between the longitude of 176° and 180°. They lie west of the International Date Line. The 2022 census determined that Tuvalu had a population of 10,643, making it the 194th most populous country, exceeding only Niue and the Vatican City in population. Tuvalu's total land area is 25.14 square kilometres (9.71 sq mi).
The first inhabitants of Tuvalu were Polynesians arriving as part of the migration of Polynesians into the Pacific that began about three thousand years ago. Long before European contact with the Pacific islands, Polynesians frequently voyaged using canoes between the islands. Polynesian navigation skills enabled them to make elaborately planned journeys in either double-hulled sailing canoes or outrigger canoes. Scholars believe that the Polynesians spread out from Samoa and Tonga into the Tuvaluan atolls, which then served as a stepping stone for further migration into the Polynesian outliers in Melanesia and Micronesia.
In 1568, Spanish explorer and cartographer Álvaro de Mendaña became the first European known to sail through the archipelago, sighting the island of Nui during an expedition he was making in search of Terra Australis. The island of Funafuti, currently serving as the capital, was named Ellice's Island in 1819. Later, the whole group was named Ellice Islands by English hydrographer Alexander George Findlay. In the late 19th century, Great Britain claimed control over the Ellice Islands, designating them as within their sphere of influence. Between 9 and 16 October 1892, Captain Herbert Gibson of HMS Curacoa declared each of the Ellice Islands a British protectorate. Britain assigned a resident commissioner to administer the Ellice Islands as part of the British Western Pacific Territories (BWPT). From 1916 to 1975, they were managed as part of the Gilbert and Ellice Islands colony.
A referendum was held in 1974 to determine whether the Gilbert Islands and Ellice Islands should each have their own administration. As a result, the Gilbert and Ellice Islands colony legally ceased to exist on 1 October 1975; on 1 January 1976, the old administration was officially separated, and two separate British colonies, Kiribati and Tuvalu, were formed. On 1 October 1978, Tuvalu became fully independent as a sovereign state within the Commonwealth, and is a constitutional monarchy with Charles III as King of Tuvalu. On 5 September 2000, Tuvalu became the 189th member of the United Nations.
The islands do not have a significant amount of soil, so the country relies heavily on imports and fishing for food. Licensing fishing permits to international companies, grants and aid projects, and remittances to their families from Tuvaluan seafarers who work on cargo ships are important parts of the economy. Because it is a low-lying island nation, Tuvalu is extremely vulnerable to sea level rise due to climate change. It is active in international climate negotiations as part of the Alliance of Small Island States.
Additional Information
Tuvalu is a country in the west-central Pacific Ocean. It is composed of nine small coral islands scattered in a chain lying approximately northwest to southeast over a distance of some 420 miles (676 km).
The de facto capital is the village of Vaiaku, where most government offices are located. It is on Fongafale islet, a constituent part of Funafuti Atoll. Together with what is now Kiribati (formerly the Gilbert Islands), Tuvalu formed the British Gilbert and Ellice Islands Colony before separately gaining its independence in 1978.
The group includes both atolls and reef islands. The atolls—Nanumea, Nui, Nukufetau, Funafuti, and Nukulaelae—have islets encircling a shallow lagoon; the reef islands—Nanumanga, Niutao, Vaitupu, and Niulakita—are compact with a fringing reef. The islands are low-lying, most being 13 to 16 feet (4 to 5 meters) above sea level. There are no rivers; rain catchment and wells provide the only fresh water. Rainfall averages 100 inches (2,500 mm) in the north and 125 inches (3,175 mm) in the south. The prevailing winds are southeast trades; westerly storms occur from November to February. Daytime temperatures range from 80 to 85 °F (27 to 29 °C).
Because the soils are porous, agriculture is limited. Coconut palms thrive, and breadfruit trees, pandanus, taro, and bananas are grown. Pigs and chickens are raised, and seabirds, fish, and shellfish are caught for food. The islands increasingly depend on imported food.
People
The Tuvaluans are Polynesian, and their language, Tuvaluan, is closely related to Samoan. Nui, however, was heavily settled in prehistoric times by Micronesians from the Gilbert Islands (now Kiribati). English is taught in the schools and widely used. The vast majority of the population belongs to the Church of Tuvalu (the former Ellice Islands Protestant Church).
Although most people live on the outer islands in extended family households clustered into villages, about one-third of the population lives on Funafuti, the center of government and commerce. Population growth has been slowed by family planning; life expectancy at birth is about 60 years. About 10 percent of the population lives overseas, either pursuing education, working in the Nauru phosphate industry, or working on merchant ships.
Economy
Most Tuvaluans are subsistence farmers and are aided by remittances from relatives working overseas. A small quantity of copra is produced for export, the sale of stamps accounts for modest earnings, and fees are collected from foreign fishing fleets, but the country depends heavily on foreign aid. It imports most of its food, fuel, and manufactured goods. Fiji, Australia, New Zealand, and Japan are among the country’s major trade partners. Retailing is handled by community-based cooperative societies. Tuvalu uses Australian currency but also issues its own coinage. There is a single bank, a joint government-commercial venture.
Tuvalu has air links with Kiribati and Fiji; for international shipping, it depends on irregular regional services. Seaplanes have been used for interisland travel, but generally the outer islands depend on a single government vessel. Motorcycles are common on Funafuti, but there are few automobiles.
Government and society
Tuvalu is a constitutional monarchy within the Commonwealth, with the British monarch (through a governor-general) as head of state. The government is a parliamentary democracy with a unicameral legislature elected by universal adult suffrage. There are no political parties: the prime minister is chosen by and from the legislature. Tuvalu is a member of the South Pacific Forum.
Cultural life
The Tuvaluan lifestyle has been Westernized to an extent, but Western-style amenities are few. Only Funafuti has a regular electricity supply; the government publishes a brief news sheet, but there is no newspaper; a few motion pictures are shown; satellite television service is available only by subscription; and there is only a single radio station. Most Tuvaluans live in villages of a few hundred people, tend their gardens, and fish from handcrafted canoes. Traditional music and dancing still enjoy a strong following, along with Western forms. Volleyball, football (soccer), and cricket are popular. Tuvaluan life, despite modernization, still rests on a firm traditional base that emphasizes the importance of community consensus and identity.
History of Tuvalu
The first settlers were from Samoa and probably arrived in the 14th century ad. Smaller numbers subsequently arrived from Tonga, the northern Cook Islands, Rotuma, and the Gilbert Islands. Niulakita, the smallest and southernmost island, was uninhabited before European contact; the other islands were settled by the 18th century, giving rise to the name Tuvalu, or “Cluster of Eight.”
Europeans first discovered the islands in the 16th century through the voyages of Álvaro de Mendaña de Neira, but it was only from the 1820s, with visits by whalers and traders, that they were reliably placed on European charts. In 1863 labor recruiters from Peru kidnapped some 400 people, mostly from Nukulaelae and Funafuti, reducing the population of the group to less than 2,500. A few were later recruited for plantations in Queensland, Australia, as well as in Fiji, Samoa, and Hawaii. Concern over labor recruiting and a desire for protection helps to explain the enthusiastic response to Samoan pastors of the London Missionary Society who arrived in the 1860s. By 1900, Protestant Christianity was firmly established.
With imperial expansion the group, then known as the Ellice Islands, became a British protectorate in 1892 and part of the Gilbert and Ellice Islands Colony in 1916. There was a gradual expansion of government services, but most administration was through island governments supervised by a single district officer based in Funafuti. Ellice Islanders sought education and employment at the colonial capital in the Gilbert group or in the phosphate industry at Banaba or Nauru. During World War II, U.S. forces were based on Nanumea, Nukufetau, and Funafuti, but hostilities did not reach the group.
From the 1960s, racial tension and rivalries over employment emerged between Gilbertese and Ellice Islanders. Ellice Islanders’ demands for secession resulted in a referendum in 1974, transition to separate colonial status between October 1975 and January 1976, and independence as Tuvalu in 1978. After independence the main priorities were to establish the infrastructure for a separate, if small, nation, and to seek foreign assistance to match political independence with economic viability.
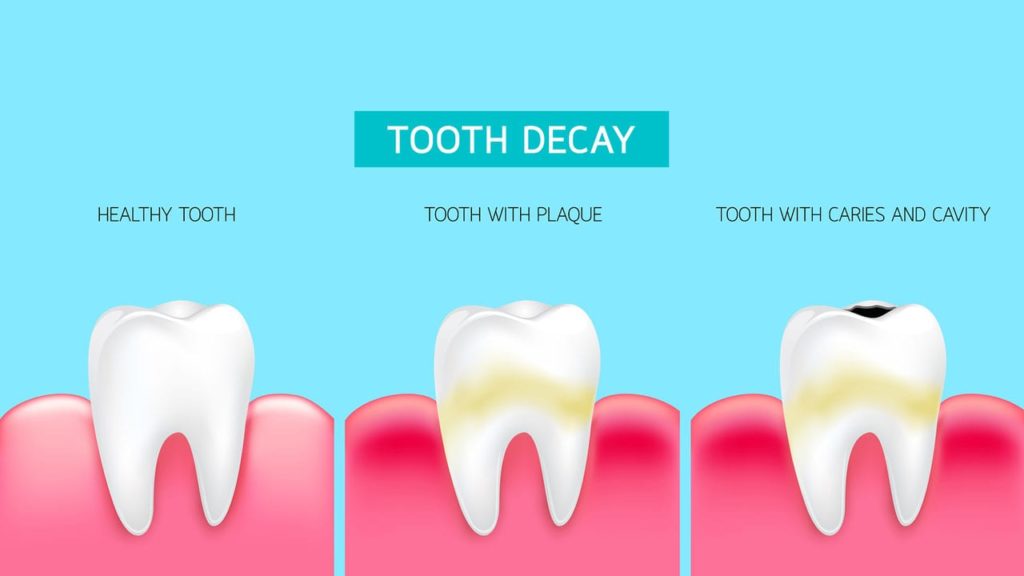
#6 Science HQ » Tooth Decay » Yesterday 17:09:44
- Jai Ganesh
- Replies: 0
Tooth Decay
Gist
Tooth decay (dental caries) is the destruction of tooth enamel caused by acids from plaque-forming bacteria feeding on sugars. Key symptoms include toothaches, sensitivity, and white/brown stains. Treatments include fluoride, fillings, crowns, or root canals. It progresses through demineralization, enamel decay, dentin decay, and pulp damage.
Tooth decay is caused by bacteria in your mouth feeding on sugars and starches, producing acids that wear down tooth enamel, forming cavities. Poor dental hygiene allows plaque (a sticky film of bacteria and food debris) to build up, and frequent snacking on sugary/starchy foods creates more acid attacks, leading to enamel erosion and holes in the teeth.
Summary
Tooth decay, also known as caries, is the breakdown of teeth due to acids produced by bacteria. The resulting dental cavities may be many different colors, from yellow to black. Symptoms may include pain and difficulty eating. Complications may include inflammation of the tissue around the tooth, tooth loss and infection or abscess formation. Tooth regeneration is an ongoing stem cell–based field of study that aims to find methods to reverse the effects of decay; current methods are based on easing symptoms.
The cause of cavities is acid from bacteria dissolving the hard tissues of the teeth (enamel, dentin, and cementum). The acid is produced by the bacteria when they break down food debris or sugar on the tooth surface. Simple sugars in food are these bacteria's primary energy source, and thus a diet high in simple sugar is a risk factor. If mineral breakdown is greater than buildup from sources such as saliva, caries results. Risk factors include conditions that result in less saliva, such as diabetes mellitus, Sjögren syndrome, and some medications. Medications that decrease saliva production include psychostimulants, antihistamines, and antidepressants. Dental caries are also associated with poverty, poor cleaning of the mouth, and receding gums resulting in exposure of the roots of the teeth.
Prevention of dental caries includes regular cleaning of the teeth, a diet low in sugar, and small amounts of fluoride. Brushing one's teeth twice per day, and flossing between the teeth once a day is recommended. Fluoride may be acquired from water, salt or toothpaste among other sources. Treating a mother's dental cavities may decrease the risk in her children by decreasing the number of certain bacteria she may spread to them. Screening can result in earlier detection. Depending on the extent of destruction, various treatments can be used to restore the tooth to proper function, or the tooth may be removed. There is no known method to grow back large amounts of tooth. The availability of treatment is often poor in the developing world. Paracetamol (acetaminophen) or ibuprofen may be taken for pain.
Worldwide, approximately 3.6 billion people (48% of the population) have dental caries in their permanent teeth as of 2016. The World Health Organization estimates that nearly all adults have dental caries at some point in time. In baby teeth it affects about 620 million people or 9% of the population. They have become more common in both children and adults in recent years. The disease is most common in the developed world due to greater simple sugar consumption, but less common in the developing world. Caries is Latin for "rottenness".
Details
Tooth decay is the breakdown or destruction of tooth enamel, the hard outer surface of a tooth. Tooth decay can lead to cavities, also called dental caries. These are holes in the teeth. Cavities can get bigger with time if left untreated. A cavity can reach deep within a tooth, where the nerve endings are, leading to pain and sensitivity.
What causes tooth decay in a child?
Tooth decay is caused by bacteria and other things. It can happen when foods containing carbohydrates (sugars and starches) are left on the teeth. Such foods include milk, soda, raisins, candy, cake, fruit juices, cereals, and bread. Bacteria that normally live in the mouth change these foods, making acids. The combination of bacteria, food, acid, and saliva form a substance called plaque that sticks to the teeth. Over time, the acids made by the bacteria eat away at the tooth enamel, causing cavities.
Which children are at risk for tooth decay?
* All children have bacteria in their mouth. So all children are at risk for tooth decay. But the following may raise your child’s risk for it:
* High levels of the bacteria that cause cavities
* A diet high in sugars and starches
* Water supply that has limited or no fluoride in it
* Poor oral hygiene
* Less saliva flow than normal
What are the symptoms of tooth decay in a child?
Tooth decay may be a bit different for each child. Here is a common way that teeth develop decay and cavities:
* White spots begin to form on the teeth in areas affected. These spots mean that the enamel is starting to break down. They may lead to early sensitivity in the teeth.
* An early cavity is seen on the tooth. It has a light brown color.
* The cavity becomes deeper. It turns a darker shade of brown to black.
The symptoms of tooth decay and cavities vary from child to child. Cavities don’t always cause symptoms. Sometimes children don’t know they have a cavity until their dentist finds it. But your child may feel:
* Pain in the area around the tooth
* Sensitivity to certain foods, such as sweets and hot or cold drinks
How is tooth decay diagnosed in a child?
Your child’s dentist can often diagnose tooth decay based on:
* A complete history of your child
* An exam of your child’s mouth (oral cavity)
* Dental X-rays
How is tooth decay treated in a child?
Treatment will depend on your child’s symptoms, age, oral hygiene, and general health. It will also depend on how severe the condition is.
For children, some early tooth decay may be managed with conservative methods such as removal of plaque, cleansing the dental decay, remineralizing the teeth, use of supplemental fluoride, and dental sealants.
In most cases, treatment will require removing the decayed part of the tooth and replacing it with a filling. Fillings are materials placed in teeth to repair damage caused by tooth decay. They are also called restorations. There are different types of fillings:
* Direct restorations. These need a single visit to place a filling directly into a prepared hole. These fillings may be made out of silver, fine glass powders, acrylic acids, or resin. They are often tooth-colored.
* Indirect restorations. These may require 2 or more visits. They include inlays, onlays, veneers, crowns, and bridges. These are constructed with gold, base metal alloys, ceramics, or composites. Many of these materials can look like natural tooth enamel.
How can I help prevent tooth decay in my child?
You can help prevent tooth decay in your child with these simple steps:
* Start brushing your child’s teeth as soon as the first tooth appears. Brush the teeth, tongue, and gums for 2 minutes twice a day with a fluoride toothpaste. Or watch as your child brushes their teeth.
* For children younger than 3 years old, use only a small amount of toothpaste, about the size of a grain of rice. Starting at age 3, your child can use a pea-sized amount of toothpaste.
* Floss your child’s teeth daily after age 2.
* Make sure your child eats a well-balanced diet. Limit snacks that are sticky and high in sugars. These include chips, candy, cookies, cake, and soda drinks.
* Prevent the transfer of bacteria from your mouth to your child's. Don't share eating utensils. And don’t clean your baby’s pacifier with your saliva.
* If your child uses a bottle at bedtime, only put water in it. Juice and formula contain sugars that can lead to tooth decay.
* Talk with your child’s healthcare provider or dentist about using a fluoride supplement if you live in an area without fluoridated water. Also, ask about dental sealants and fluoride varnish. Both are put on the teeth.
* Schedule routine dental cleanings and exams for your child every 6 months.
Key points about tooth decay in children
* Tooth decay is the breakdown of tooth enamel. It can lead to holes in the teeth called cavities or dental caries.
* Tooth decay is caused by bacteria in the mouth. These bacteria make a sticky substance called plaque that can eat away at a tooth’s enamel.
* Poor oral hygiene can raise your child’s risk for tooth decay.
* A dentist can diagnose tooth decay with an exam and X-rays.
* Treatment may require removing the decayed part of the tooth and replacing it with a filling.
Additional Information
Cavities are holes, or areas of tooth decay, that form in your teeth surfaces. Causes include plaque buildup, eating lots of sugary snacks and poor oral hygiene. Treatments include dental fillings, root canal therapy and tooth extraction. The sooner you treat a cavity, the better your chance for a predictable outcome and optimal oral health.
Overview:
What is a cavity?
A cavity is a hole in a tooth that develops from tooth decay. Cavities form when acids in your mouth wear down (erode) your tooth’s hard outer layer (enamel). Anyone can get a cavity. Proper oral hygiene and regular dental cleanings can prevent cavities.
Another name for tooth cavities is dental caries.
Types of cavities
Cavities can start on any tooth surface. Here are common types of cavities and where they occur:
* Smooth surface: This slow-growing cavity dissolves tooth enamel. You can prevent it — and sometimes reverse it — with proper oral hygiene. People in their 20s often develop this form of tooth decay between their teeth.
* Pit and fissure decay: Cavities form on the top part of your tooth’s chewing surface. Decay also can affect the front side of your back teeth. Pit and fissure decay tends to start during the teenage years and progresses quickly.
* Root decay: Adults who have receding gums are more prone to root decay. Gum recession exposes your teeth roots to dental plaque and acid. Root decay is difficult to prevent and treat. (If you’re prone to gum recession, ask your dentist if you should schedule an appointment with a periodontist.)
How common are cavities?
More than 80% of Americans have at least one cavity by the time they enter their mid-30s. Cavities are one of the most common chronic diseases affecting people of all ages.
Who might get a cavity?
Tooth decay can happen at any age, although cavities are more common in children. This is because many children don’t brush properly or regularly enough and they tend to consume more sugary foods and drinks.
Many adults also get cavities. Sometimes, new decay develops around the edges of cavities treated in childhood. Adults are also more likely to have receding gums. This condition exposes your teeth roots to plaque, which can cause cavities.
Symptoms and Causes:
What are the signs of cavities?
Tooth decay on the outer enamel surface doesn’t usually cause pain or symptoms. You’re more likely to experience symptoms as decay reaches beyond the enamel into the dentin and pulp.
Cavity symptoms include:
* Bad breath or a bad taste in your mouth.
* Bleeding gums or other signs of gum disease.
* Facial swelling.
* Toothache or mouth pain.
* Tooth sensitivity to hot or cold foods or drinks.
Tooth decay stages
Cavities can affect all layers of your tooth.
There are five main tooth decay stages:
1. Demineralization: During this first stage, you may notice small, white, chalky spots on your tooth. This is due to the breakdown of minerals in your tooth enamel.
2. Enamel decay: Left untreated, tooth decay progresses and continues to break down your enamel. At this point, cavities (holes) may become noticeable. White spots may turn to a light brownish color.
3. Dentin decay: Dentin is the layer just beneath your tooth enamel. It’s much softer than your enamel. So, once plaque and bacteria reach this layer, cavities form faster. At this stage, you may notice teeth sensitivity. The spots on your teeth may also turn to a darker brown.
4. Pulp damage: Your tooth pulp is the innermost layer of your tooth. It contains nerves and blood vessels that transport nutrients and keep your tooth alive. When cavities reach your pulp, you may feel pain. You may also start to notice redness and swelling in the gums around your tooth. The spots on your tooth may turn darker brown or black.
5. Abscessed tooth: Left untreated, a deep cavity can cause infection. This results in a pocket of pus that forms at the tip of your tooth root (periapical abscess). Symptoms may include pain that radiates into your jaw or face. You may also develop facial swelling and swollen lymph nodes in your neck. At this point, a tooth abscess can spread to surrounding tissues and other areas of your body. In rare cases, infection can even spread to your brain or to your bloodstream (sepsis).
What causes cavities?
Many factors play a role in the development of cavities.
Here’s how it works:
* Bacteria in your mouth feed on sugary, starchy foods and drinks (fruit, candy, bread, cereal, sodas, juice and milk). The bacteria convert these carbohydrates into acids.
* Bacteria, acid, food and saliva mix to form dental plaque. This sticky substance coats your teeth.
* Without proper brushing and flossing, acids in plaque dissolve tooth enamel, creating cavities, or holes, in the enamel surface.
What are the risk factors for cavities?
Certain factors increase your risk of cavities, including:
* Dry mouth (xerostomia). Certain conditions (like Sjögren’s syndrome), or medications (like antidepressants) can make you more likely to develop dry mouth.
* Consuming sugary, starchy foods or drinks and snacking between meals.
* Family history of tooth decay.
* Gum recession.
* Previous radiation therapy to treat head and neck cancer.
Are cavities contagious?
While you can’t “catch” a cavity, the bacteria that cause cavities can pass from one person to another. In turn, any bacteria you pick up from another person (from kissing, for instance) can lead to tooth decay and other oral health issues over time.
Diagnosis and Tests:
How are cavities diagnosed?
Twice-a-year dental checkups are the best way to catch cavities early, before they worsen or grow larger. A dentist will use a number of instruments to examine your teeth. A tooth with a cavity will feel softer when your dentist probes it.
Your dentist may also take dental X-rays. These images show cavities before the decay is visible.
Management and Treatment:
How do you get rid of cavities?
Tooth decay treatment depends on the severity of your condition.
Cavity treatments include:
* Fluoride.
* Fillings.
* Root canal therapy.
* Tooth extraction.
* Fluoride
In the very early stages of tooth decay, fluoride treatments can repair damaged enamel — a process called remineralization. This can reverse the early signs of cavities. You may need prescription toothpaste and mouthwash, as well as fluoride treatments at the dental office.
Dental fillings
Once a hole forms in your tooth, a dentist drills out the decayed tissue and fills the hole. Dental fillings consist of composite resin (a tooth-colored material), silver amalgam or gold.
Root canal therapy
Root canal therapy relieves pain from advanced tooth decay. Endodontists (specialists who treat issues that affect a tooth’s root) usually perform the procedure. During root canal treatment, an endodontist removes the tooth pulp, then fills the canals and pulp chamber with gutta-percha (a special filling material). In some cases, you might also need a dental crown to strengthen the affected tooth.
Tooth extraction
If root canal therapy isn’t possible, your healthcare provider may recommend tooth extraction (pulling the tooth). You may need a dental bridge or dental implant to replace a pulled permanent tooth. Your dentist can tell you about your specific options.
Outlook / Prognosis:
What can I expect if I have cavities?
When tooth decay goes untreated for too long, you can lose a large portion of your tooth and need an extraction. Advanced tooth decay can lead to a severe infection inside your tooth and under your gums (tooth abscess). This infection can spread throughout your body. Rarely, infection from a tooth abscess can be fatal.
What’s the outlook for people with cavities?
Most people with cavities don’t experience any long-term problems. Because cavities develop slowly, it’s important to get regular dental checkups. Fluoride treatments can stop tooth decay in its early stages. Once tooth decay advances to the root, you risk losing the tooth or developing a painful abscess (infection).
#7 Re: Jai Ganesh's Puzzles » General Quiz » Yesterday 16:13:31
Hi,
#10787. What does the term in Geography Desert pavement mean?
#10788. What does the term in Geography Desert varnish mean?
#8 Re: Jai Ganesh's Puzzles » English language puzzles » Yesterday 16:02:53
Hi,
#5993. What does the noun krill mean?
#5994. What does the noun kudos mean?
#9 Re: Jai Ganesh's Puzzles » Doc, Doc! » Yesterday 15:43:57
Hi,
#2593. What does the medical term Failure to thrive (FTT) mean?
#10 Re: Jai Ganesh's Puzzles » 10 second questions » Yesterday 15:28:39
Hi,
#9879.
#11 Re: Jai Ganesh's Puzzles » Oral puzzles » Yesterday 15:16:32
Hi,
#6372.
#12 Re: Exercises » Compute the solution: » Yesterday 14:45:57
Hi,
2733.
#13 Re: This is Cool » Miscellany » Yesterday 00:06:18
2519) Potassium Dichromate
Gist
Potassium dichromate is a bright red-orange, odorless crystalline inorganic compound and a strong, non-deliquescent oxidizing agent commonly used in laboratories and industries. As a hexavalent chromium compound, it is highly toxic, corrosive, and a significant allergen. It is widely used for chrome tanning, dyeing, photography, and as a primary analytical standard in redox titrations.
Potassium dichromate is a strong oxidizing agent used in leather tanning (chrome tanning), wood staining (darkening), photography, and as a reagent in analytical chemistry for titrations and purity tests (Schwertzer's solution). It's also used in manufacturing matches, fireworks, and pigments, as a catalyst, and to make chromic acid for etching, though its toxicity has restricted many of these applications.
Summary
Potassium dichromate (K2Cr2O7) is a bright red-orange crystalline compound widely used in laboratories and industries as an oxidizing agent. Its non-deliquescent nature makes it preferable to other dichromates. However, as a hexavalent chromium compound, it is highly toxic and harmful to health.
Potassium dichromate, an inorganic compound with a bright orange colour, is widely used as an oxidizing agent in laboratories and industries. It is produced by reacting chromates with sodium or potassium carbonate. Although it is less potent than potassium permanganate, it is valued for its stability in acid and resistance to light and organic matter. Potassium dichromate is used in cleaning glassware, etching, and photographic screen printing. However, it is highly toxic and must be handled carefully due to its health hazards. As a dichromic acid dipotassium salt, it is one of the most significant and widely used chromium compounds in inorganic chemistry.
Physical Properties of Potassium Dichromate
Appearance: Solid at room temperature with bright orange crystals.
Odor and Taste: Odorless with a bitter taste.
Toxicity: It is toxic and can irritate the eyes.
Combustibility: Non-combustible but prone to rusting.
Melting and Boiling Points: Melts at 398°C and decomposes upon boiling at 500°C.
Solubility: Solubility increases in water at higher temperatures but is insoluble in alcohol and acetone.
Refractive Index: 1.738.
Structure: The chromium ion in potassium dichromate has a tetrahedral coordinate geometry. The crystalline structure is triclinic.
Details
Potassium dichromate is the inorganic compound with the formula K2Cr2O7. An orange solid, it is used in diverse laboratory and industrial applications. As with all hexavalent chromium compounds, it is chronically harmful to health. It is a crystalline ionic solid with a very bright, red-orange color. The salt is popular in laboratories because it is not deliquescent, in contrast to the more industrially relevant salt sodium dichromate.
Niche or archaic uses
Potassium dichromate has few major applications, as the sodium salt is dominant industrially. The main use is as a precursor to potassium chrome alum, used in leather tanning.
Photography and printing
In 1839, Mungo Ponton discovered that paper treated with a solution of potassium dichromate was visibly tanned by exposure to sunlight, the discoloration remaining after the potassium dichromate had been rinsed out. In 1852, Henry Fox Talbot discovered that exposure to ultraviolet light in the presence of potassium dichromate hardened organic colloids such as gelatin and gum arabic, making them less soluble.
These discoveries soon led to the carbon print, gum bichromate, and other photographic printing processes based on differential hardening. Typically, after exposure, the unhardened portion was rinsed away with warm water, leaving a thin relief that either contained a pigment included during manufacture or was subsequently stained with a dye. Some processes depended on the hardening only, in combination with the differential absorption of certain dyes by the hardened or unhardened areas. Because some of these processes allowed the use of highly stable dyes and pigments, such as carbon black, prints with an extremely high degree of archival permanence and resistance to fading from prolonged exposure to light could be produced.
Dichromated colloids were also used as photoresists in various industrial applications, most widely in the creation of metal printing plates for use in photomechanical printing processes.
Chromium intensification or Photochromos uses potassium dichromate together with equal parts of concentrated hydrochloric acid diluted down to approximately 10% v/v to treat weak and thin negatives of black and white photograph roll. This solution reconverts the elemental silver particles in the film to silver chloride. After thorough washing and exposure to actinic light, the film can be redeveloped to its end-point yielding a stronger negative which is able to produce a more satisfactory print.
A potassium dichromate solution in sulfuric acid can be used to produce a reversal negative (that is, a positive transparency from a negative film). This is effected by developing a black and white film but allowing the development to proceed more or less to the end point. The development is then stopped by copious washing and the film then treated in the acid dichromate solution. This converts the silver metal to silver sulfate, a compound that is insensitive to light. After thorough washing and exposure to actinic light, the film is developed again allowing the previously unexposed silver halide to be reduced to silver metal. The results obtained can be unpredictable, but sometimes excellent results are obtained producing images that would otherwise be unobtainable. This process can be coupled with solarisation so that the end product resembles a negative and is suitable for printing in the normal way.
Cr(VI) compounds have the property of tanning animal proteins when exposed to strong light. This quality is used in photographic screen-printing.
In screen-printing a fine screen of bolting silk or similar material is stretched taut onto a frame similar to the way canvas is prepared before painting. A colloid sensitized with a dichromate is applied evenly to the taut screen. Once the dichromate mixture is dry, a full-size photographic positive is attached securely onto the surface of the screen, and the whole assembly exposed to strong light – times vary from 3 minutes to a half an hour in bright sunlight – hardening the exposed colloid. When the positive is removed, the unexposed mixture on the screen can be washed off with warm water, leaving the hardened mixture intact, acting as a precise mask of the desired pattern, which can then be printed with the usual screen-printing process.
Analytical reagent
Because it is non-hygroscopic, potassium dichromate was a common reagent in classical "wet tests" in analytical chemistry.
Aldehyde test
In an aqueous solution the color change exhibited can be used as a test to distinguish aldehydes from ketones. Aldehydes reduce dichromate from the +6 to the +3 oxidation state, changing the solution color from orange to green. A ketone will show no such change because it cannot be oxidized further, and so the solution will remain orange.
Wood treatment
Potassium dichromate is used to stain certain types of wood by darkening the tannins in the wood. It produces deep, rich browns that cannot be achieved with modern color dyes. It is a particularly effective treatment on mahogany.
Natural occurrence
Potassium dichromate occurs naturally as the rare mineral lópezite. It has only been reported as vug fillings in the nitrate deposits of the Atacama Desert of Chile and in the Bushveld igneous complex of South Africa.
Safety
Potassium dichromate is a prevalent allergen in patch tests (4.8%). Its presence in cement can cause contact dermatitis in construction workers after extended exposure. In general, it is one of the most common causes of chromium dermatitis. Aquatic organisms are vulnerable to poisoning by dichromate salts, but far less so than organic pollutants.
As with other Cr(VI) compounds, potassium dichromate is carcinogenic. The compound is also corrosive and exposure may damage eyes. Human exposure further causes impaired fertility.
Additional Information
Potassium Dichromate is an orange to red colored, crystalline, inorganic compound that emits toxic chromium fumes upon heating. Potassium dichromate is highly corrosive and is a strong oxidizing agent. This substance is used in wood preservatives, in the manufacture of pigments and in photomechanical processes, but is mainly replaced by sodium dichromate. Potassium dichromate primarily affects the respiratory tract causing ulcerations, shortness of breath, bronchitis, pneumonia and asthma but can also affect the gastrointestinal tract, liver, kidneys and immune system. This substance is a known human carcinogen and is associated with an increased risk of developing lung cancer and cancer of the sinonasal cavity.
Potassium dichromate or anhydrochromate is prepared by adding to the neutral yellow chromate of potassium in solution, a moderate quantity of one of the stronger acids.
Potassium permanganate is commercially prepared by mixing a solution of potassium hydroxide and powdered manganese oxide with oxidizing agents like potassium chlorate.
Preparation of Potassium Dichromate – K2Cr2O7
* Potassium dichromate is an important chemical used in industries as an oxidizing agent and for the preparation of many other compounds.
* Dichromates are usually prepared from chromates and this is obtained by the combination of chromite ore with sodium/potassium carbonate in the presence of air.
Applications of Potassium Dichromate
The primary application of K2Cr2O7 is in the preparation of potassium chrome alum, a compound which is used extensively in the tanning of leather. Chromic acid can also be prepared from this compound. Potassium dichromate is known to be used in the production of cement since it improves the texture and the density of the cement mixture.
Another important application of potassium dichromate is in the photography industry, where it is used in combination with a powerful mineral acid as an oxidizing agent for photographic screen printing. Since it is non-hygroscopic in nature, this compound is also employed for several wet tests in the field of analytical chemistry.
Frequently Asked Questions – FAQs
Q1: What is the use of potassium dichromate?
A1. It is used in many applications as an oxidizing agent and is also used in the preparation of different products such as waxes, paints, glues, etc. Potassium dichromate is carcinogenic and highly toxic as a compound of hexavalent chromium.
Q2: What does the potassium dichromate test for?
A2. For organic chemistry, potassium dichromate is an oxidizing agent that is milder than potassium permanganate. It is used for the oxidation of alcohol. This converts primary alcohols into aldehydes and carboxylic acids under more pressing conditions.
Q3: Is potassium dichromate light-sensitive?
A3. Clear, light-sensitive orange crystals. Potassium dichromate is used in cotton dyeing as chromium mordant. In black and white image processing, potassium dichromate is used as an intensifier.
Q4: What is the charge of potassium dichromate?
A4. K2Cr2O7 is the molecular formula. A reddish-brown colour as a solid and a molecular weight of 294.18 grams per mole is the physical properties of potassium dichromate. Potassium dichromate is also referred to as a compound of hexavalent chromium, and chromium oxidation is 6+.

#14 Re: Dark Discussions at Cafe Infinity » crème de la crème » Yesterday 00:05:57
2456) Hans Krebs
Gist:
Work
Nutrients are broken down in our cells to release energy for the construction of cells. After Albert Szent-Györgyi identified several important reactions in these metabolic processes, in 1937 Hans Krebs was able to present a complete picture of an important part of metabolism—the citric acid cycle. In this process, which is cyclical and has several steps, nutrients are converted to other molecules with a large amount of chemical energy. The latter are ultimately converted into adenosine triphosphate (ATP), which provides chemical energy to facilitate other biochemical processes in the cell.
Summary
Sir Hans Adolf Krebs (born Aug. 25, 1900, Hildesheim, Ger.—died Nov. 22, 1981, Oxford, Eng.) was a German-born British biochemist who received (with Fritz Lipmann) the 1953 Nobel Prize for Physiology or Medicine for the discovery in living organisms of the series of chemical reactions known as the tricarboxylic acid cycle (also called the citric acid cycle, or Krebs cycle). These reactions involve the conversion—in the presence of oxygen—of substances that are formed by the breakdown of sugars, fats, and protein components to carbon dioxide, water, and energy-rich compounds.
At the University of Freiburg (1932), Krebs discovered (with the German biochemist Kurt Henseleit) a series of chemical reactions (now known as the urea cycle) by which ammonia is converted to urea in mammalian tissue; the urea, far less toxic than ammonia, is subsequently excreted in the urine of most mammals. This cycle also serves as a major source of the amino acid arginine.
The son of a Jewish physician, Krebs was forced in 1933 to leave Nazi Germany for England, where he continued his research at the University of Cambridge (1933–35). At Sheffield University, Yorkshire (1935–54), Krebs measured the amounts of certain four-carbon and six-carbon acids generated in pigeon liver and breast muscle when sugars are oxidized completely to yield carbon dioxide, water, and energy.
In 1937 Krebs demonstrated the existence of a cycle of chemical reactions that combines the end-product of sugar breakdown, later shown to be an “activated” form of the two-carbon acetic acid, with the four-carbon oxaloacetic acid to form citric acid. The cycle regenerates oxaloacetic acid through a series of intermediate compounds while liberating carbon dioxide and electrons that are immediately utilized to form high-energy phosphate bonds in the form of adenosine triphosphate (ATP; the chemical-energy reservoir of the cell). The discovery of the tricarboxylic acid cycle, which is central to nearly all metabolic reactions and the source of two-thirds of the food-derived energy in higher organisms, was of vital importance to a basic understanding of cell metabolism and molecular biology.
Krebs served on the faculty of the University of Oxford from 1954 to 1967. He wrote (with the British biochemist Hans Kornberg) Energy Transformations in Living Matter (1957) and also coauthored (with Anne Martin) Reminiscences and Reflections (1981). He was knighted in 1958, and the Royal Society awarded him its Copley Medal in 1961.
Details
Sir Hans Adolf Krebs, (25 August 1900 – 22 November 1981) was a German-British biologist, physician and biochemist. He was a pioneer scientist in the study of cellular respiration, a biochemical process in living cells that extracts energy from food and oxygen and makes it available to drive the processes of life. He is best known for his discoveries of two important sequences of chemical reactions that take place in the cells of nearly all organisms, including humans, other than anaerobic microorganisms, namely the citric acid cycle and the urea cycle. The former, often eponymously known as the "Krebs cycle", is the sequence of metabolic reactions that allows cells of oxygen-respiring organisms to obtain far more ATP from the food they consume than anaerobic processes such as glycolysis can supply; and its discovery earned Krebs a Nobel Prize in Physiology or Medicine in 1953. With Hans Kornberg, he also discovered the glyoxylate cycle,[8] a slight variation of the citric acid cycle found in plants, bacteria, protists, and fungi.
Krebs died in 1981 in Oxford, where he had spent 13 years of his career from 1954 until his retirement in 1967 at the University of Oxford.
Biography:
Early life and education
Krebs was born in Hildesheim, Germany, to Georg Krebs, an ear, nose, and throat surgeon, and Alma Krebs (née Davidson). He was of Jewish ancestry and was the middle of three children. He had an elder sister, Elisabeth, and a younger brother, Wolfgang.
Krebs attended school at the Gymnasium Andreanum in his home town. Near the end of World War I, in September 1918, six months short of completing his secondary school education, he was conscripted into the Imperial German Army. He was allowed to take an emergency examination for his high school diploma, which he passed with such a high score that he suspected the examiners of being "unduly lenient and sympathetic". With the end of the war two months later, his conscription ended.
Krebs decided to follow his father's profession and entered the University of Göttingen in December 1918 to study medicine. In 1919, he transferred to the University of Freiburg. In 1923, he published his first scientific paper on a tissue staining technique. He did this work under the guidance of Wilhelm von Mollendorf starting it in 1920. He completed his medical course in December 1923. To obtain a Doctor of Medicine degree, and a medical license, he spent one year at the Third Medical Clinic in the University of Berlin. By then he had turned his professional goal from becoming a practising physician to becoming a medical researcher, particularly in biochemistry. In 1924, he studied at the Department of Chemistry at the Pathological Institute of the Charité Hospital, in Berlin, for training in chemistry and biochemistry. He earned his MD degree in 1925 from the University of Hamburg.
Career
In 1926, Krebs joined Otto Heinrich Warburg as a research assistant at the Kaiser Wilhelm Institute for Biology in Dahlem, Berlin. He was paid 4800 marks per year. After four years in 1930, with 16 publications to his credit, his mentor Warburg urged him to move on and he took up the position of Assistant in the Department of Medicine at the Municipal Hospital in Altona (now part of Hamburg). The next year he moved to the Medical Clinic of the University of Freiburg. At Freiburg, he was in charge of about 40 patients, and was at liberty to do his own research. Before a year was over at Freiburg, he, with research student Kurt Henseleit, published their discovery of the ornithine cycle of urea synthesis, which is the metabolic pathway for urea formation. It is now known as the urea cycle, and is sometimes also referred to as the Krebs–Henseleit cycle. Together they also developed a complex aqueous solution (a buffer), or perfusion ex vivo, for studying blood flow in arteries, which is now called the Krebs–Henseleit buffer. In 1932, he published the basic chemical reactions of the urea cycle, which established his scientific reputation.
Krebs's life as a respected German scientist came to an abrupt halt in 1933 because of his Jewish ancestry. With the rise of Hitler's Nazi Party to power, Germany decreed the Law for the Restoration of the Professional Civil Service, which decreed the removal of all non-Germans, and anti-Nazis, from professional occupations. Krebs received his official dismissal from his job in April 1933, and his service was terminated on 1 July 1933. An admirer, Sir Frederick Gowland Hopkins at the University of Cambridge, immediately came to his rescue, and persuaded the university to recruit Krebs to work with him in the Department of Biochemistry. By July 1933, he was settled in Cambridge with financial support from the Rockefeller Foundation.
Although Germany restricted him to bringing only his personal belongings, he was fortunate that the government agents allowed him to take his equipment and research samples to England. They proved to be pivotal to his later discoveries, especially the manometer developed by Warburg specifically for the measurement of oxygen consumption in thin slices of tissues; it was the basis for his research.
He was appointed as Demonstrator in biochemistry in 1934, and in 1935 the University of Sheffield offered him a post of Lecturer in Pharmacology, with a more spacious laboratory and double the salary. He worked there for 19 years. The University of Sheffield opened a Department of Biochemistry, now Department of Molecular Biology and Biotechnology, in 1938 and Krebs became its first Head, and eventually a Professor in 1945. During his time it became one of the leading departments of biochemistry in the world. Krebs took over the running of the Sorby Research Institute in 1943. In 1944, the British Medical Research Council established the MRC Unit for Cell Metabolism Research at Sheffield, and Krebs was appointed the Director. With this, his laboratory became so large that the locals jokingly nicknamed it "Krebs's Empire".
He moved with his MRC unit to the University of Oxford in 1954 as Whitley Professor of Biochemistry, the post he held until his retirement in 1967. The editorial board of Biochemical Journal extended their good wishes on his retirement, but in return he promised to keep them busy, by producing scientific papers. He continued his research, and took his MRC unit to the Nuffield Department of Clinical Medicine at the Radcliffe Infirmary, Oxford. From there he published over 100 research papers.

#15 Jokes » Nut Jokes - I » Yesterday 00:05:37
- Jai Ganesh
- Replies: 0
Q: How do squirrels remember where they stored their nuts during winter?
A: They use acorn-yms.
* * *
Q: Why do squirrels swim on there back?
A: To keep their nuts dry!
* * *
Q: What do you call a squirrel with no nuts?
A: Female Squirrel.
* * *
Q: Why can't you be friends with a squirrel?
A: They drive everyone nuts.
* * *
Q: Why shouldn't you hate a tree?
A: There might be a squirrel in there looking for nuts.
* * *
#16 Dark Discussions at Cafe Infinity » Comedies Quotes - III » Yesterday 00:02:57
- Jai Ganesh
- Replies: 0
Comedies Quotes - III
1. I was making a lot of 8mm home movies, since I was twelve, making little dramas and comedies with the neighborhood kids. - Steven Spielberg
2. I played comedies and dramas. - William Shatner
3. I think there are opportunities for women in comedies - how zany is up to them. - Jennifer Aniston
4. When I tried to play characters that strayed from who I am it ended in disaster. People didn't expect me in comedies or musicals. - Sylvester Stallone
5. Usually comedy is only available to us ladies in the romantic comedy. That's why I hate romantic comedies. - Sandra Bullock
6. I personally don't like to go see romantic comedies. But people do want to see them, and they seem to want to see me in them. - Matthew McConaughey
7. There weren't roles for females in comedies for a really long time. - Sandra Bullock
8. I have a lot more fun making comedies because there's a levity on the set, and I find it difficult to go to work and, you know, cry for 12 hours. - Megan Fox.
#17 This is Cool » San Marino » 2026-03-11 17:49:16
- Jai Ganesh
- Replies: 0
San Marino
Gist
San Marino is one of the world's smallest countries, ranking as the fifth smallest globally by area (around 61 sq km or 24 sq miles) and the third smallest in Europe after Vatican City and Monaco, entirely surrounded by Italy. It's also recognized as the world's oldest republic, founded in 301 AD.
The Oldest Republic
Established in 301 AD, this tiny nation has maintained its independence and self-governance for over 1,700 years. Its rich history and the preservation of its ancient traditions make San Marino a captivating destination for history enthusiasts.
Summary
San Marino, officially the Republic of San Marino (RSM), is a landlocked country in Southern Europe, completely surrounded by Italy. Located on the northeastern slopes of the Apennine Mountains, it is the larger of two microstates within Italy, the other being Vatican City. San Marino is the fifth-smallest country in the world, with a land area of just over 61 sq km (23.5 sq mi) and a population of 34,042 as of 2025. Its capital, the City of San Marino, sits atop Monte Titano, while its largest settlement is Dogana, in the municipality of Serravalle.
San Marino claims to have been founded in AD 301 and to be the oldest extant sovereign state, and the oldest constitutional republic. It is named after Saint Marinus, a stonemason from the Roman island of Rab (in present-day Croatia), who is supposed in mythic accounts to have established a monastic community on Monte Titano. The country has a rare constitutional structure: the Grand and General Council, a democratically elected legislature, selects two heads of state, the Captains Regent, every six months. They are chosen from opposing political parties, and serve concurrently with equal powers and preside over several institutions of state, including the Grand and General Council. Only the Federal Council of Switzerland also follows that structure, except with seven heads of state, and different responsibilities and functions.
San Marino is a member of the Council of Europe and uses the euro as its official currency, but is not part of the European Union. The official language is Italian, although the traditional regiolect is Sammarinese, a dialect of Romagnol. Its economy is based on finance, industry, services, retail, and tourism, and it ranks among the wealthiest countries in the world by GDP (PPP) per capita. San Marino was also the first currently-existing state to abolish the death penalty (in 1865), and in 2025 was ranked 29th on the Human Development Index.
Details
San Marino is a small, landlocked republic situated on the slopes of Mount Titano, on the Adriatic side of central Italy between the Emilia-Romagna and Marche regions and surrounded on all sides by the republic of Italy. It is the smallest independent state in Europe after Vatican City and Monaco and, until the independence of Nauru (1968), the smallest republic in the world.
Geography
San Marino has an irregular rectangular form with a maximum length of 8 miles (13 km), northeast to southwest. It is crossed by the Marano and Ausa (Aussa) streams, which flow into the Adriatic Sea, and by the stream of San Marino, which falls into the Marecchia River. The landscape is dominated by the huge, central limestone mass of Mount Titano (2,424 feet [739 meters]); hills spread out from it on the southwest, whereas the northeastern part gently slopes down toward the Romagna plain and the Adriatic coast. The silhouette of Mount Titano, with its three summits crowned by ancient triple fortifications, may be seen from many miles away. In 2008 Mount Titano and the historic center of San Marino were designated a UNESCO World Heritage site.
The climate is mild and temperate, with maximum temperatures in the high 70s F (about 26 °C) in summer and the high teens F (about −7 °C) in winter. Annual rainfall ranges between about 22 inches (560 mm) and 32 inches (800 mm). Vegetation is typical of the Mediterranean zone, with variations due to elevation, and includes olive, pine, oak, ash, poplar, fir, and elm, as well as many kinds of grasses and flowers. Besides domestic and farmyard animals, moles, hedgehogs, foxes, badgers, martens, weasels, and hares are found. Indigenous birds and birds of passage are plentiful.
Although traces of human presence from both prehistoric and Roman times exist in the territory, Mount Titano and its slopes are known to have been populated, with certainty, only after the arrival of St. Marinus and his followers. San Marino citizens, or Sammarinesi, make up more than four-fifths of the country’s population, with Italians composing most of the remainder. Thousands of Sammarinesi reside abroad, principally in Italy, the United States, France, and Argentina. Nearly nine-tenths of San Marino’s citizens are Roman Catholics, though there is no official religion. The official language is Italian. A widely spoken dialect has been defined as Celto-Gallic, akin to the Piedmont and Lombardy dialects as well as to that of Romagna.
Because centuries-long quarrying has exhausted Mount Titano’s stone and ended the craft that depended upon it, the territory is now without mineral resources. All electrical power is transferred via electrical grid from Italy, San Marino’s main trading partner. The country’s principal resources are industry, tourism, commerce, agriculture, and crafts. Manufactures include electronics, paint, cosmetics, ceramics, jewelry, and clothing. Ceramic and wrought-iron articles, as well as modern and reproduction furniture, are among San Marino’s traditional craft products. Fine printing, particularly of postage stamps, is a consistent source of revenues. Banking is a vital industry. In 2002 San Marino replaced the Italian lira with the euro as its national currency.
Tourism is the sector of greatest expansion, and it makes a major contribution to the inhabitants’ income. Alongside traditional excursion tourism, there is convention-type tourism, based on modern hotel facilities, as well as residential tourism.
Agriculture, although no longer the principal economic resource in San Marino, remains vital. Wheat, grapes, and barley are the chief crops; dairying and livestock also are important. About three-fourths of the land is given to permanent cultivation.
The capital, San Marino city, is set high on the western side of Mount Titano, beneath the fortress crowning one of its summits, and is encircled by triple walls. Borgo Maggiore, farther down the slope, was for centuries San Marino’s commercial center, and Serravalle, beneath its castle of the Malatesta family, is agricultural and industrial. San Marino is overwhelmingly urban in character, and those three cities are home to nearly two-thirds of San Marino’s population. Most of San Marino’s landscape is agricultural in character, but industrial concerns have intruded on the centuries-old forms of agricultural life.
The San Marino constitution, originating from the Statutes of 1600, provides for a parliamentary form of government. The Great and General Council (Parliament) has 60 members, elected every five years by all adult citizens. It has legislative and administrative powers and every six months nominates the two captains regent (capitani reggenti), who hold office for that period and may not be elected again until three years have elapsed. The Great and General Council is headed by the captains regent, who are heads of state and of the administration. The Congress of State, a council of ministers, is composed of 10 members, elected by the Great and General Council from among its members, and constitutes the central organ of executive power. Each member has charge of a ministerial department.
Social programs for the citizens of San Marino are extensive. The state attempts to keep unemployment in check by seeking to provide employment for those who cannot find work with private concerns. All citizens (who make social security contributions) receive free, comprehensive, high-quality medical care and assistance in sickness, accident, and old age, as well as family allowances. The state aids home ownership through its buildings schemes. Education is free and compulsory up to age 16. The University of San Marino was founded in 1985. A public security force of about 50 persons provides national defense.
A network of roads connects San Marino with the surrounding regions of Italy. Motorcoach services connect San Marino city with Rimini, Italy, and, in summer, directly with the Adriatic coast. The main airport serving San Marino is the Federico Fellini International Airport in Rimini. There are no railroads, but the capital is reached from Borgo Maggiore by means of a cable railway.
History
The Republic of San Marino traces its origin to the early 4th century ce when, according to tradition, St. Marinus and a group of Christians settled there to escape persecution. The Castellum Sancta Marini is mentioned in the Liber Pontificalis (“The Book of the Pontiffs”) in 755; the oldest document in the republican archives mentions the abbot of San Marino in 885. By the 12th century San Marino had developed into a commune ruled by its own statutes and consuls. The commune was able to remain independent despite encroachments by neighboring bishops and lords, largely because of its isolation and its mountain fortresses. Against the attacks of the Malatesta family, who ruled the nearby seaport of Rimini, San Marino enjoyed the protection of the rival family of Montefeltro, who ruled Urbino. By the middle of the 15th century, it was a republic ruled by a Grand Council—60 men taken from the Arengo, or Assembly of Families. Warding off serious attacks in the 16th century (including an occupation by Cesare Borgia in 1503), San Marino survived the Renaissance as a relic of the self-governing Italian city-states. Rule by an oligarchy and attempts to annex it to the Papal States in the 18th century marked the decline of the republic.
When Napoleon invaded Italy, he respected the independence of the republic and even offered to extend its territory (1797). The Congress of Vienna (1815), at the end of the Napoleonic Wars, also recognized its independent status. During the 19th-century movement for Italian unification, San Marino offered asylum to revolutionaries, among them Giuseppe Garibaldi. After Italy became a national state, a series of treaties (the first in 1862) confirmed San Marino’s independence. In World War II, San Marino remained neutral, but it was the target of a British bombing raid in 1944 and was briefly occupied by both the Germans and the Allies later that year.
Additional Information
Europe attracts more international tourists than any other region of the world, according to the United Nations World Tourism Organization. The staggering 616 million people that visited the continent last year faced the tough choice of dozens of destinations, each offering stimulating history, diverse classes of creatives, and epic landscapes. France seduced the most travelers by far, but what about last place?
Hovering on a cliff encircled by Italy, the tiny landlocked country of San Marino holds the title of the least visited country in Europe, just a dot on the map of only 23.6 square miles. Here’s why travelers of all types should visit the under the radar microstate.
For History Buffs
Founded in the fourth century and one of the world’s oldest republics, San Marino survived from the time when city-states proliferated across Europe—a critical stage for developing democratic models across the globe. Ramble around the car-free capital also named San Marino, a UNESCO World Heritage site with a medievalized layout punctuated by three imposing fortresses standing testimony to a turbulent past.
Fer Epic Landscapes
The Mount Titano, part of the Apennine range, dominates San Marino's landscape surrounded by Italy with clear views all the way to the Adriatic Sea. Old stone benches pepper the slopes offering places to bask in the greenery stretching to the outlying villages. Ride the funicular from one such town, Borgo Maggiore, to the historic center for sweeping views of Italy in every direction.
For Foodies
All the rules of northern Italian food apply here too, with a strong tradition in cheesemaking. Sammarinese cuisine, heavy on pasta and meat dishes, balances the rich and fresh with locally-sourced ingredients. The area holds particular fondness for the filled flatbread called piada, similar to a piadina from the encompassing Emilia-Romagna region. Don’t forget the wine: San Marino produced wine for almost two thousand years, aging the bottles in the area caves for optimal temperatures.
For Architecture Fans
Visitors weave through time in the living history museum of the historic capital, home to 14th and 16th century convents, 18th century Titano Theatre, and a neoclassical basilica built in the 19th century. The centerpiece Palazzo Pubblico echos Florence’s Palazzo Vecchio on a much smaller scale.
For Savvy Shoppers
The tax-free policy of San Marino makes shopping cheaper than nearby Italy. Mid-century modern ceramics captivate collectors, along with postage stamps created in the late 19th century for use only within the state's borders.
For Day-Trippers
San Marino may not be a member of the European Union but enjoys open borders with Italy for tourists staying less than 10 days. The ideal location makes for easy day trips from cities like Florence or Bologna, both located less than three hours away.
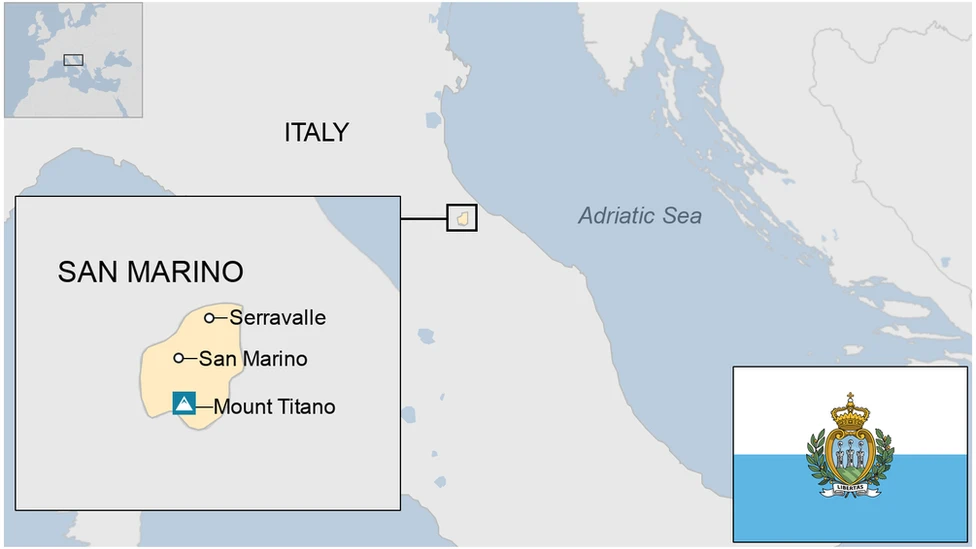
#18 Science HQ » Pyorrhea (Periodontitis) » 2026-03-11 16:45:52
- Jai Ganesh
- Replies: 0
Pyorrhea (Periodontitis)
Gist
Pyorrhea, or periodontitis, is a severe, chronic bacterial infection of the gums that damages soft tissue and destroys the bone supporting the teeth, often causing tooth loss. Key symptoms include bleeding gums, persistent bad breath, receding gums, and loose teeth. It is primarily caused by untreated plaque buildup, leading to inflammation and infection.
Pyorrhea, also known as severe gum disease or periodontal disease, is primarily caused by poor oral hygiene leading to plaque and tartar buildup, which irritates the gums and allows bacteria to infect the supporting structures, resulting in inflammation, bone loss, and eventual tooth loosening. Contributing factors include smoking, genetics, certain medical conditions, hormonal changes, and injury to the gums.
Summary
Periodontal disease, also known as gum disease, is a set of inflammatory conditions affecting the tissues surrounding the teeth. In its early stage, called gingivitis, the gums become swollen and red and may bleed. It is considered the main cause of tooth loss for adults worldwide. In its more serious form, called periodontitis, the gums can pull away from the tooth, bone can be lost, and the teeth may loosen or fall out. Halitosis (bad breath) may also occur.
Periodontal disease typically arises from the development of plaque biofilm, which harbors harmful bacteria such as Porphyromonas gingivalis and Treponema denticola. These bacteria infect the gum tissue surrounding the teeth, leading to inflammation and, if left untreated, progressive damage to the teeth and gum tissue. Recent meta-analysis have shown that the composition of the oral microbiota and its response to periodontal disease differ between men and women. These differences are particularly notable in the advanced stages of periodontitis, suggesting that sex-specific factors may influence susceptibility and progression. Factors that increase the risk of disease include smoking, diabetes, HIV/AIDS, and almost any autoimmune disease, family history, high levels of homocysteine in the blood and certain medications. Diagnosis is by inspecting the gum tissue around the teeth both visually and with a probe and X-rays looking for bone loss around the teeth.
Treatment involves good oral hygiene and regular professional teeth cleaning. Recommended oral hygiene include daily brushing and flossing. In certain cases antibiotics or dental surgery may be recommended. Clinical investigations demonstrate that quitting smoking and making dietary changes enhance periodontal health. Globally, 538 million people were estimated to be affected in 2015 and has been known to affect 10–15% of the population generally. In the United States, nearly half of those over the age of 30 are affected to some degree and about 70% of those over 65 have the condition. Males are affected more often than females.
Details
Contrary to what one might imagine, it is a widespread disease. widespread disease. In fact, 15% of the population suffers from a severe form of periodontitis and about 50% is affected in various ways, 15% of the population suffers from a severe form of periodontitis and about 50% are affected in various ways.. This is a problem that should not be underestimated, as it also has a strong impact on a person's overall health.
What is periodontitis?
Periodontitis, or periodontal disease, is a polymicrobial polymicrobial infection that affects the periodontium i.e., the tissues and tissues and structures that support the teeth: gums, bone and periodontal ligaments..
Periodontitis damages all periodontal tissues, but, depending on the level of infection, it has different degrees of severity, has different degrees of severity.
When not properly treated, periodontitis can progress from the first stage, which may correspond to gingivitis, to a may correspond to gingivitisto the most to the most severe stage of the disease, also called periodontitiswhich manifests itself with the loss of teeth. loss of the dental pieces more or less rapid.
Underestimated, but widespread, periodontal disease is a very serious pathology of the oral cavity.
Unfortunately, many patients tend to overlook the symptoms of periodontitis, many patients tend to overlook the symptoms of periodontitis and only visit the dentist in the acute phase of the disease. and only visit the dentist in the acute phase of the disease.
Symptoms of periodontal disease
Symptoms of periodontal disease should never be underestimated, as they always lead to worsening and chronic periodontal disease. lead to worsening and chronicity of the disease.
The main symptoms of periodontitis are:
* Bleeding gums
* Dental hypersensitivity to heat and cold
* Pain and hypersensitivity of the gums
* Flaccidity of the gums
* Feeling of having "longer" teeth
* Sensation of having teeth that move
* Sensation of teeth shifting position
* Halitosis
Neglecting even one of these symptoms can lead to the development of periodontitis. development of periodontitis and aggravation of periodontal disease.
In the presence of one or several symptoms, it is necessary to immediately contact a specialized dentist who, by means of an adequate analysis of the oral cavity, can correlate the signs detected with the possible pathology.
Causes
The main causes of periodontitis are:
* Daily oral hygiene daily deficient or absent.
* The consequent accumulation of dental biofilm.
* Appearance of tartar.
Although subjective factors of various kinds, related to the condition and characteristics of the patient's organism, may also contribute, periodontal disease is mainly determined by the lack of proper care, both on a daily basisThe lack of proper periodontal care, both on a daily basis as well as periodic visits to the dentist.
Treatment
When gingivitis progresses to periodontitis, treatment becomes much more complicated. Only the dentist and hygienist can provide periodontal treatment, which requires special dental procedures and may require oral surgery.which requires special dental procedures and may require oral surgery. If the dentist concludes that periodontitis is present, treatment will depend on the severity of the infection. Options include, but are not limited to, the following:
* Scaling and root planing: In this two-step procedure to treat periodontitis, the dentist will scrapes tartar buildup from the teeth above and below the gum line (scaling). (scaling). Next, the dental specialist polishes away the roughness of the tooth roots, which reduces the accumulation of bacteria and therefore plaque and tartar.
* Flap surgery : If gum inflammation and pockets near the teeth persist after a deep cleaning procedure, your dentist may recommend flap surgery. Flap surgery, a common procedure to treat periodontitis, is performed by a specialist called a periodontist. During flap surgery tartar is removed from the pockets along the teeth. The pockets are then sutured so that the gum tissues can reattach to the teeth.. The reduction of the pockets makes brushing and flossing easier and more comfortable.
* Grafts Grafting: Severe cases of periodontitis may require bone or tissue grafts to replace the infected one, may require bone or tissue grafts to replace infected bone or tissue. The grafting may consist of a technique called "guided tissue regeneration"in which a small piece of membrane is inserted between the jawbone and the gum to allow the bone and tissue to regenerate. Guided tissue regeneration prevents the gum tissue from expanding in the area that the bone should occupy, so that the bone and tissue grafts have the space they need to grow.
Prevention
From infancy, it is possible to prevent periodontitis: It is possible to prevent periodontitis, counteract the appearance of its main symptoms and avoid an inflammatory process that can degenerate into an acute bacterial infection with a few simple measures:
* Attend regular and continuous professional hygiene sessions. professional hygiene with a specialized professional.
* After every meal, practice proper daily dental hygiene at home. at home.
* Pay close attention to attention to the symptoms of periodontal of periodontal disease.
Contrary to popular belief, pyorrhea is a disease that can also affect children and adolescents. can also affect children and adolescents. It can also affect children and adolescents, with varying degrees of pathology and, if not effectively treated, can have aggressive recurrences in the course of development.
To prevent the appearance of the main symptoms of periodontal disease in children and adolescents, it is necessary to educate them from a very young age, after every meal, in a correct and regular daily oral hygiene and to submit them regularly to professional oral hygiene sessions in a dental clinic they trust.
Types of periodontitis
From the clinical point of view, depending on the symptoms and the aggressiveness of the pathology we can have:
* Chronic periodontitis
Chronic periodontitis is the most common form of periodontal disease, and occurs much more frequently in people over the age of 45.and occurs much more frequently in people over 45 years of age. This chronic disease is characterized by inflammation of the gums inflammation of the gums and progressive destruction of gum and bone tissue. It may appear as if the teeth are lengthening, but in reality the gums are gradually receding.
Chronic periodontitis causes an inflammatory reaction of the tissues that support the tooth.. It causes loss of attachment and bone resorption and is classified as an infectious disease. It is most commonly diagnosed in adults, although children and adolescents can also develop it.. To evaluate its severity, we look at the percentage of affected foci (especially visible due to hemorrhage): if 30% or more are affected, it is said to be generalized and if 30% or less of the foci are affected, it is localized.
* Ulcerative-necrotic periodontitis
Ulcerative-necrotic periodontitis is a very severe form, characterized by the presence of true ulcers at the gum level very severe form, characterized by the presence of true ulcers at the gum level, with necrosis of the entire supporting apparatus of the tooth. Although rare, it occurs in young adulthood, with a higher incidence in developing countries, with risk factors such as malnutrition, lack of oral hygiene, immune depression and chronic systemic diseases.. Along with the typical symptoms, fever, enlarged cervical lymph nodes and general malaise may also occur.
Aggressive periodontitis
Aggressive periodontitis is a rare form of rare form of periodontitis which mainly affects children or the elderly; It is characterized by a fairly rapid and extensive destructive process, especially affecting incisors and molars.It is characterized by a rather rapid and extensive destructive process, especially affecting the incisors and molars.
Additional Information
Have you ever experienced how suddenly and without prior pain a tooth moves or even falls out? You may be suffering from periodontitis or gum disease without knowing it. If you want to know what it consists of and how to prevent and treat it, keep reading.
Currently, the term “pyorrhea” is obsolete in dentistry, but perhaps many of you have heard it over the years. The word “pyorrhea” is still commonly used to refer to gum disease, although the term we currently use in dentistry to refer to it is “periodontitis.”
Pyorrhea or periodontitis is an infectious disease and the main cause of tooth loss along with cavities. Its great danger lies in the fact that it is a disease that does not cause excessive pain or too severe discomfort, so it often goes unnoticed or is easily normalized.
It is a chronic inflammatory condition of the tissue surrounding our teeth, resulting in progressive destruction of the periodontal ligament and the alveolar bone that supports our teeth.
The main difference from gingivitis is that gingivitis involves inflammation of the gums but does not involve bone destruction, whereas periodontitis or pyorrhea does involve bone destruction.
When periodontal pockets form, which are an accumulation of bacteria below the gum line, their action causes damage to dental structures, leading to the deterioration of the bone supporting our teeth.
Why does periodontitis occur?
As we mentioned, being an infectious disease, the main cause of its appearance is the accumulation of bacterial plaque due to poor oral hygiene. If we do not correctly remove this plaque, we will cause inflammation of our gums in the short term and hardening over time, adhering to our teeth and forming what we call tartar (calculus), which once attached to the tooth, we will not be able to remove it with conventional brushing and will require professional dental hygiene.
How can we know if we have periodontitis?
To detect if we are suffering from periodontitis, the most common symptoms are gum inflammation and a change in its color, becoming reddish or violet. Of course, another clear symptom is bleeding gums when brushing, bad breath, discomfort when chewing, or noticing that some teeth are loose.
Sometimes spaces between the teeth may also appear, and in some cases, abscesses or overgrowth in the gums. But undoubtedly, bleeding is the first warning sign. Bleeding gums do not directly mean that we have pyorrhea; it could be gingivitis. However, it will serve as an alert for us to immediately consult our specialist for a correct diagnosis and intervention before the disease progresses to a more severe stage.
What are the risk factors?
Any of us can suffer from periodontitis if we do not take proper care of ourselves, but there are certain risk factors that can accelerate the disease or simply increase the risk of suffering from it.
Chronic gingivitis, smoking, hormonal changes in women such as pregnancy or menopause, old age, substance abuse, lack of vitamin C, or diseases that weaken our defenses (diabetes, arthritis, Crohn’s disease, leukemia, HIV, oncological treatments). In these cases, prevention should be even more thorough to avoid future complications.
Periodontitis Treatment
As we have already mentioned, the main cause of periodontitis is poor oral hygiene, so the key to stopping the appearance or progression of the disease will undoubtedly be to have proper oral hygiene.
Periodontal disease can lead to serious consequences for our health, so it is important to detect it as soon as possible to be able to treat it and prevent it from becoming chronic.
The first step is to establish a clear diagnosis elaborated by a professional, to assess what our best options are and find a solution adapted to our needs.
* Once diagnosed, we can make a prognosis for our teeth and
* realize a treatment plan tailored to our needs. It usually starts with deep dental hygiene to remove calculus adhered to our teeth and below the gums.
And from there, the key factor will be to correct our poor hygiene habits as soon as possible and maintain proper maintenance by our specialist, attending regular check-ups as recommended. We will have to learn to correctly use our toothbrush, use dental floss and interdental brushes to complete our daily hygiene, and visit our dentist regularly to take care of the residues we cannot reach.
We must bear in mind that periodontitis is a chronic disease, so once diagnosed, maintenance visits for professional hygiene should be regular to halt its progression. A professional cleaning every 3, 4, or 6 months is recommended depending on each patient’s needs.

#19 Re: Jai Ganesh's Puzzles » General Quiz » 2026-03-11 16:08:27
Hi,
#10785. What does the term in Geography Depression (geology) mean?
#10786. What does the term in Geography Desert mean?
#20 Re: Jai Ganesh's Puzzles » English language puzzles » 2026-03-11 15:49:22
Hi,
#5991. What does the verb (used with obeject) invoke mean?
#5992. What does the adjective irksome mean?
#21 Re: Jai Ganesh's Puzzles » Doc, Doc! » 2026-03-11 15:33:02
Hi,
#2592. What does the medical term Perimetrium mean?
#22 Re: Jai Ganesh's Puzzles » 10 second questions » 2026-03-11 15:18:09
Hi,
#9878.
#23 Re: Jai Ganesh's Puzzles » Oral puzzles » 2026-03-11 14:57:59
Hi,
#6371.
#24 Re: Exercises » Compute the solution: » 2026-03-11 14:27:22
Hi,
2732.
#25 Re: This is Cool » Miscellany » 2026-03-11 00:05:09
2518) Parrot
Gist
A parrot is a colorful, intelligent bird from the order Psittaciformes, known for its strong curved beak, zygodactyl feet (two toes forward, two back), and ability to mimic sounds, including human speech, making them popular but often endangered pets found in tropical and subtropical regions. They are social creatures with diverse diets of fruits, nuts, and seeds, playing roles in ecosystems by dispersing seeds.
Can a parrot speak?
Yes, parrots can talk, but it's more accurately described as exceptional mimicry of human speech, with some species like African Greys and Amazons learning to imitate words and phrases, sometimes even using them contextually to communicate emotions or needs, driven by their strong social bonds and vocal learning abilities. They use a special vocal organ (syrinx) and a flexible tongue to shape sounds, allowing them to replicate human voices and other noises with surprising accuracy, essentially forming a social bond with their human flock.
Summary
Parrots (Psittaciformes), also known as psittacines from the name of the type genus Psittacus, are birds with a strong curved beak, upright stance, and clawed feet. They are classified in four families that contain roughly 410 species in 101 genera, found mostly in tropical and subtropical regions. The four families are the Psittaculidae (Old World parrots), Psittacidae (African and New World parrots), Cacatuidae (math), and Strigopidae (New Zealand parrots). One-third of all parrot species are threatened by extinction, with a higher aggregate extinction risk (IUCN Red List Index) than any other comparable bird group. Parrots have a generally pantropical distribution with several species inhabiting temperate regions as well. The greatest diversity of parrots is in South America and Australasia.
Parrots, along with corvids (ravens, crows, jays, and magpies), are among the most intelligent birds, and the ability of some species to imitate human speech enhances their popularity as pets. They form the most variably sized bird order in terms of length; many are vividly coloured and some, multi-coloured. Most parrots exhibit little or no sexual dimorphism in the visual spectrum.
The most important components of most parrots' diets are seeds, nuts, fruit, buds, and other plant material. A few species sometimes eat animals and carrion, while the lories and lorikeets are specialised for feeding on floral nectar and soft fruit. Almost all parrots nest in tree hollows (or nest boxes in captivity), and lay white eggs from which hatch altricial (helpless) young.
Trapping wild parrots for the pet trade, as well as hunting, habitat loss, and competition from invasive species, has diminished wild populations, with parrots being subjected to more exploitation than any other group of wild birds. As of 2021, about 50 million parrots (half of all parrots) live in captivity, with the vast majority of these living as pets in people's homes. Measures taken to conserve the habitats of some high-profile charismatic species have also protected many of the less charismatic species living in the same ecosystems.
Parrots are the only creatures that display true tripedalism, using their necks and beaks as limbs with propulsive forces equal to or greater than those forces generated by the forelimbs of primates when climbing vertical surfaces. They can travel with cyclical tripedal gaits when climbing.
Details
Parrot is a term applied to a large group of gaudy, raucous birds of the family Psittacidae. Parrot also is used in reference to any member of a larger bird group, order Psittaciformes, which includes math (family Cacatuidae) as well. Parrots have been kept as cage birds since ancient times, and they have always been popular because they are amusing, intelligent, and often affectionate. Several are astonishingly imitative of many sounds, including human speech.
The family Psittacidae numbers 333 species. The subfamily Psittacinae, the “true” parrots, is by far the largest subfamily, with members found in warm regions worldwide. These birds have a blunt tongue and eat seeds, buds, and some fruits and insects. Many members of the subfamily are known simply as parrots, but various subgroups have more specific names such as macaw, parakeet, conure, and lovebird.
The African gray parrot (Psittacus erithacus) is unsurpassed as a talker; the male can precisely echo human speech. Captive birds are alert and, compared with other parrots, relatively good-tempered. Some are said to have lived 80 years. The bird is about 33 cm (13 inches) long and is light gray except for its squared, red tail and bare, whitish face; the sexes look alike. Gray parrots are common in the rainforest, where they eat fruits and seeds; they damage crops but are important propagators of the oil palm.
Among other proficient mimics are the Amazon parrots (Amazona). The 31 species of Amazons are chunky birds, mostly 25 to 40 cm (10 to 16 inches) long, with slightly erectile crown feathers and a rather short, squared tail. Their predominantly green plumage is marked with other bright colours, chiefly on the upper head; the sexes look alike. Amazon parrots live in tropical forests of the West Indies and Mexico to northern South America. They are difficult to breed and may be aggressive as well as squawky. Common in aviaries is the blue-fronted Amazon (A. aestiva) of Brazil; it has a blue forehead, a yellow or blue crown, a yellow face, and red shoulders. The yellow-crowned parrot (A. ochrocephala) of Mexico, Central America, and from Ecuador to Brazil has some yellow on the head and neck, a red wing patch, and a yellow tail tip.
The monk, or green, parakeet (Myiopsitta monachus) is one of the hardiest parrot species. It is native to South America, but some have escaped from captivity in the United States and now nest in several states. Its large stick nest is unique among psittaciforms. Other remarkable parrots of this subfamily include the hanging parrots (Loriculus), which sleep upside-down like bats. Caiques (Pionites) are small, short-tailed South American birds similar to conures in build and habits.
For decades the night parrot, or night parakeet (Geopsittacus occidentalis), of Australia was thought to be extinct, until a dead one was found in 1990. It feeds at night on spinifex grass seeds and dozes under a tussock by day. Its nest is a twig platform in a bush and is entered by way of a tunnel. Equally unusual is the ground parrot, or ground parakeet (Pezoporus wallicus). Rare local populations exist in the wastelands of coastal southern Australia and western Tasmania. It runs in the grass, flushes like a quail, and makes a sudden deceptive pitch, and it was formerly hunted with dogs. It eats seeds and insects; its nest is a leaf-lined depression under a bush.
The lories (with short tails) and lorikeets (with longer, pointed tails) make up the Psittacidae subfamily Loriinae. The 53 species in 12 genera are found in Australia, New Guinea, and some Pacific islands. All have a slender, wavy-edged beak and a brush-tipped tongue for extracting nectar from flowers and juices from fruits.
The pygmy parrots of the subfamily Micropsittinae all belong to the genus Micropsitta. The six species are endemic to New Guinea and nearby islands. These are the smallest members of the family. They live in forests, where they eat insects and fungi.
The subfamily Nestorinae is found only in New Zealand. The kea (Nestor notabilis) occasionally tears into sheep carcasses (rarely, weakened sheep) to get at the fat around the kidneys. The kaka, N. meridionalis, a gentler forest bird, is often kept as a pet. The owl parrot, or kakapo (Strigops habroptilus), also lives only in New Zealand. It is the sole member of the subfamily Strigopinae. Rare and once thought extinct, it survives as a scant population on Stewart Island.
The math family (Cacatuidae) numbers 21 species from Australia, New Guinea, and nearby islands. The group includes the math (Nymphicus hollandicus), a smaller bird. All are crested and have heavy beaks for cracking nuts and seeds. The so-called sea parrot is unrelated to the psittaciforms.
Additional Information
The parrots are a broad order of more than 350 birds. Macaws, Amazons, lorikeets, lovebirds, math and many others are all considered parrots.
Shared Traits
Though there is great diversity among these birds, there are similarities as well. All parrots have curved beaks and all are zygodactyls, meaning they have four toes on each foot, two pointing forward and two projecting backward. Most parrots eat fruit, flowers, buds, nuts, seeds, and some small creatures such as insects.
Parrots are found in warm climates all over most of the world. The greatest diversities exist in Australasia, Central America, and South America.
Popularity as Pets
Many parrots are kept as pets, especially macaws, Amazon parrots, math, parakeets, and math. These birds have been popular companions throughout history because they are intelligent, charismatic, colorful, and musical. Some birds can imitate many nonavian sounds, including human speech. The male African gray parrot (Psittacus erithacus) is the most accomplished user of human speech in the animal world; this rain forest-dweller is an uncanny mimic.
Threats to Survival
Currently the Convention on International Trade in Endangered Species (CITES) bans the sale of any wild-caught species, yet the parrots' popularity continues to drive illegal trade.
Some parrot species are highly endangered. In other cases, once tame birds have reproduced in the wild and established thriving feral populations in foreign ecosystems. The monk (green) parakeet, for example, now lives in several U.S. states.
