Math Is Fun Forum

And I from the name of your web site that you would of course approve?!

NB: Dear Administrator - only just found this forum, and this is my first post. I hope you don't mind me including my slightly eccentric pictures, below. And, for that matter, linking to my own (tiny) web site. Not trying to steal any posters, just spread my little word. Please let me know if I'm infringing the letter or spirit of your house rules (which I will study again in a minute) and if so then whether you might be able to accept such posts as this one with appropriate modifications. Cheers! Tom

Anyway, regarding this thread...

If integration by parts is required, they want you to focus on the product rule instead of the chain rule.

Just in case a picture helps...

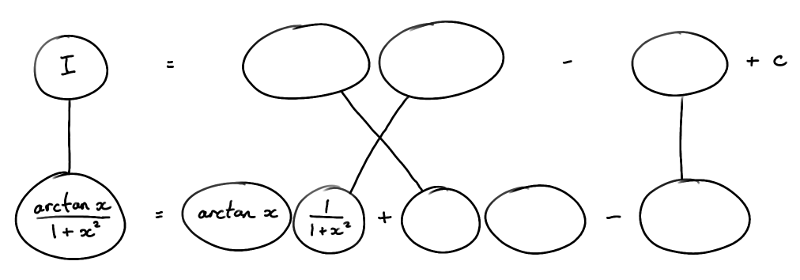
... where the triangular network is the legs-crossed version of...

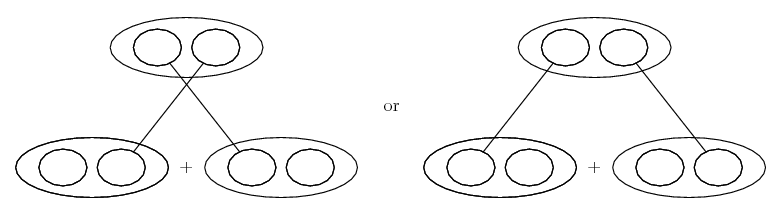
... the product rule, where straight lines differentiate downwards (integrate up) with respect to x.

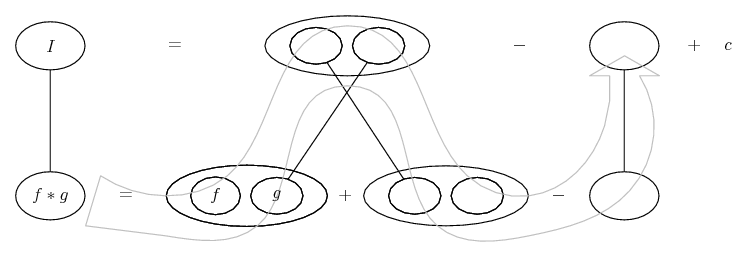
... is lazy integration by parts, doing without u and v. That is, you fill out the rest of the product-rule shape, then subtract what needs subtracting in order to keep the bottom row equal to what you started with.

Try to fill the blanks, then check below.

(By the way, I'm writing tan^-1 as 'arctan'.)

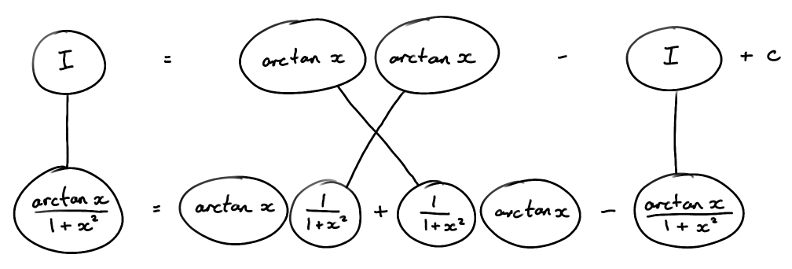
Now solve the top row for I.

On the other hand, you need the chain rule if you want to justify the derivative of arctan, as here.

_________________________________________

Don't integrate - balloontegrate!

Balloon Calculus; standard integrals, derivatives and methods

Balloon Calculus Drawing with LaTeX and Asymptote!