Math Is Fun Forum

Natkirky

Member

Registered: 2006-10-17

Posts: 21

Integration by Parts

Hi,

I am doing first year Uni maths.  I was wondering if someone could help me with the following question:

∫tan-¹x/1 + x²

I have the solution although I don't understand how to get to it.  I would be very grateful if someone could go through all the steps with me.

Thank you

gAr

Member

Registered: 2011-01-09

Posts: 3,482

Re: Integration by Parts

Hi Natkirky,

Try substitution,

Last edited by gAr (2011-05-07 23:58:17)

---

"Believe nothing, no matter where you read it, or who said it, no matter if I have said it, unless it agrees with your own reason and your own common sense"  - Buddha?

"Data! Data! Data!" he cried impatiently. "I can't make bricks without clay."

123ronnie321

Member

Registered: 2010-09-28

Posts: 128

Re: Integration by Parts

Hi Natkirky,

Here are some nice pages on integration. Do not see the solutions of the problems instantly. Give them a try first!

http://www.mathisfunforum.com/viewtopic.php?id=3299
http://www.mathisfunforum.com/viewtopic.php?id=6855

tom@ballooncalculus

Member

Registered: 2011-05-08

Posts: 4

Re: Integration by Parts

NB: Dear Administrator - only just found this forum, and this is my first post. I hope you don't mind me including my slightly eccentric pictures, below. And, for that matter, linking to my own (tiny) web site. Not trying to steal any posters, just spread my little word. Please let me know if I'm infringing the letter or spirit of your house rules (which I will study again in a minute) and if so then whether you might be able to accept such posts as this one with appropriate modifications. Cheers! Tom

Anyway, regarding this thread...

If integration by parts is required, they want you to focus on the product rule instead of the chain rule.

Just in case a picture helps...

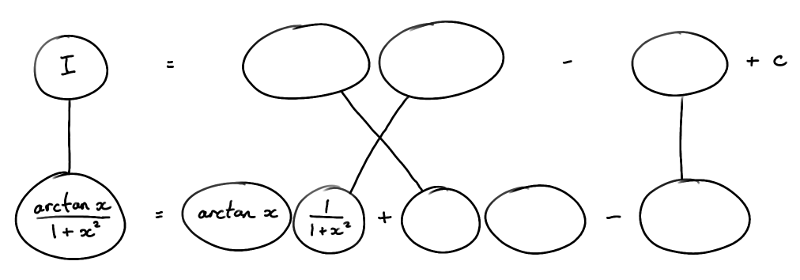
... where the triangular network is the legs-crossed version of...

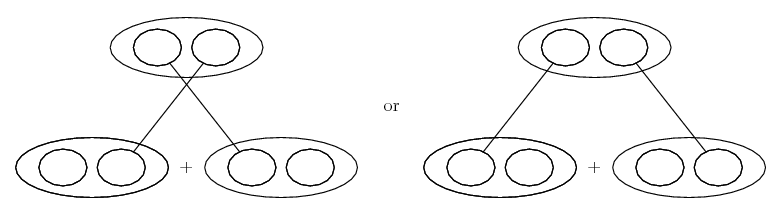
... the product rule, where straight lines differentiate downwards (integrate up) with respect to x.

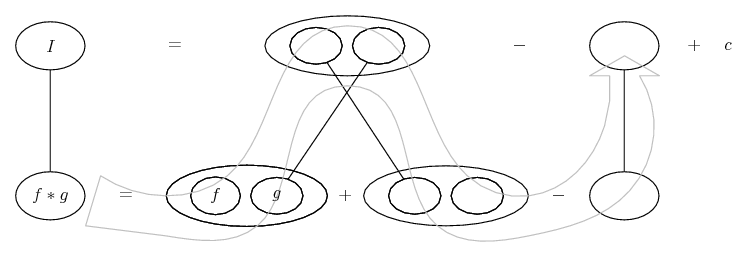
... is lazy integration by parts, doing without u and v. That is, you fill out the rest of the product-rule shape, then subtract what needs subtracting in order to keep the bottom row equal to what you started with.

Try to fill the blanks, then check below.

(By the way, I'm writing tan^-1 as 'arctan'.)

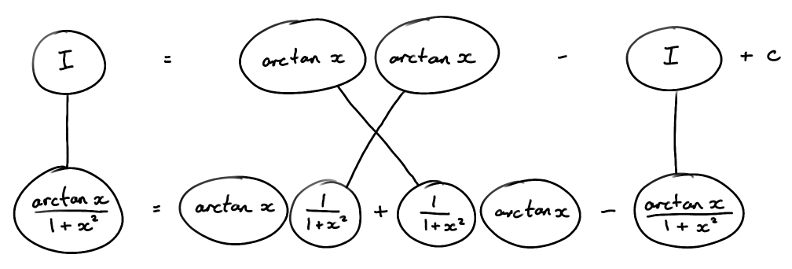
Now solve the top row for I.

On the other hand, you need the chain rule if you want to justify the derivative of arctan, as here.

_________________________________________

Don't integrate - balloontegrate!

Balloon Calculus; standard integrals, derivatives and methods

Balloon Calculus Drawing with LaTeX and Asymptote!

bobbym

bumpkin

From: Bumpkinland

Registered: 2009-04-12

Posts: 109,606

Re: Integration by Parts

Hi tom@ballooncalculus;

Welcome to the forum. I can not speak for MIF but your post is okay with me.

---

In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.

tom@ballooncalculus

Member

Registered: 2011-05-08

Posts: 4

Re: Integration by Parts

Cheers!

Bob

Administrator

Registered: 2010-06-20

Posts: 10,624

Re: Integration by Parts

hi Tom,

Welcome to the Forum. 

Am I to conclude from your 'name' that you do all calculus with balloons? 

Bob

---

Children are not defined by school ...........The Fonz
You cannot teach a man anything;  you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you!  …………….Bob

tom@ballooncalculus

Member

Registered: 2011-05-08

Posts: 4

Re: Integration by Parts

And I from the name of your web site that you would of course approve?!

Last edited by tom@ballooncalculus (2011-05-09 01:51:11)

Bob

Administrator

Registered: 2010-06-20

Posts: 10,624

Re: Integration by Parts

hi tom@ballooncalculus

Yes, I approve.  But my preference is chocolate theory as you will see if you search my posts.

And I always try to wrap up the maths in a picture if I can.

name of your web site

Not mine personally as I'm a relative newcomer here.  But I feel I fit in,  due to the welcome I have received.

Bob

Last edited by Bob (2011-05-09 08:27:42)

---

Children are not defined by school ...........The Fonz
You cannot teach a man anything;  you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you!  …………….Bob

tom@ballooncalculus

Member

Registered: 2011-05-08

Posts: 4

Re: Integration by Parts

my preference is chocolate theory as you will see if you search my posts.

Well I've browsed, without (chocolate-related) enlightenment. Although I would certainly expect to like that theory...

Bob

Administrator

Registered: 2010-06-20

Posts: 10,624

Re: Integration by Parts

Ah, well,  have a look at

http://www.mathisfunforum.com/viewtopic.php?id=14693

and the related

http://www.mathisfunforum.com/viewtopic.php?id=14725  post #15

You have to understand this is a theory 'work in progress'.  In addition to 'fractions', I'm hoping to extend it into 'topology' and 'algebra'.  Then onwards to take over all aspects of maths .......

Bob

---

Children are not defined by school ...........The Fonz
You cannot teach a man anything;  you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you!  …………….Bob