Posts by Line

Line · Help Me !

But 2*(a+b+c+d+...) (which is the result of the projection of length X=1 upon itself) is actually 1 only if the projected non-straight line is collapsed into length 0.

This is definitely not the case in the diagram above (there are infinitely many non-straight lines, where each one of them has length X=1).

So, I still do not understand how 2*(a+b+c+d+...)=X by your string of notations.

Moreover, if length X=1 is defined in terms of the set of all R members in [0,1], and [0,1] is invariant (exactly as X=1 is invariant in the diagram above), then how exactly |R| is collapsed into cardinality 1 (which is the cardinality of the set with a single member (the vertex at the bottom of the big triangle))?

Line · Help Me !

Hi,

Here is some diagram:

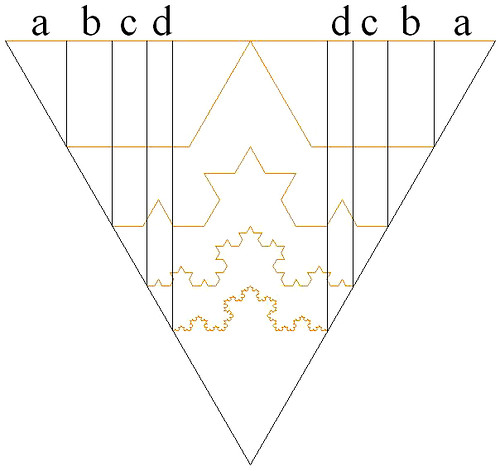
Let the length of the straight orange line be X=1

The rest of the non-straight orange lines (in this particular case, the non-straight orange lines have forms of different degrees of Koch fractal) are actually the same line with length X=1 ,such that its end points are projected upon itself, and as a result we get the convergent series 2*(a+b+c+d+...).

By using the definition of Limit as used by Real-analysis X-2*(a+b+c+d+...)=0, but 2*(a+b+c+d+...) is the projected result of infinite amount of non-straight orange lines (where each one of them has the length X=1).

Since length X=1 is invariant upon infinite amount of non-straight orange lines, how (by using the definition of Limit as used by Real-analysis) one concludes that 2*(a+b+c+d+...) = X ?

Math Is Fun Forum

#1 Re: Help Me ! » A question about limits » 2014-10-18 23:05:08

#2 Help Me ! » A question about limits » 2014-10-18 09:34:04

Board footer