Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#1 This is Cool » Finished my tutorial on using y=mx+b for webpage font sizes » 2022-02-28 03:35:08
- renevanderlende
- Replies: 1
Hi All!
After nearly 2 years of messing around with various forms of y=mx+b I finally managed to finish my tutorial on how to use it for font sizes in web development Responsive and Fluid Typography.
Thanks to 'Math is Fun' and especially Bob.
#2 Help Me ! » Finding a generic mathematical way to 'slow down' sequence progression » 2022-01-20 14:10:34
- renevanderlende
- Replies: 0
Currently there is a lot to do about 'Modular Scales' (basically 'size ratios') to create appealing font sizes for a website.
The principle is rather easy: with a base font size, create a sequence of font sizes give a chosen ratio:
scale
ratio factor description
----- ------ -----------
16:15 1.067 minor second => growing a font size nice and slow
9:8 1.125 major second
6:5 1.2 minor third
5:4 1.25 major third
4:3 1.333 perfect fourth => still appealing, but already growing too fast for comfort
√2:1 1.414 aug. fourth / dim. fifth
3:2 1.5 perfect fifth
8:5 1.6 minor sixth
1.618:1 1.618 golden ratio (ϕ)/Fibonacci
5:3 1.667 major sixth
16:9 1.778 minor seventh
15:8 1.875 major seventh
2:1 2 octave
5:2 2.5 major tenth
8:3 2.667 major eleventh
e 2.718 Euler's number (2.718281828..)
3:1 3 major twelfth
4:1 4 double octave => massive effect as each next font size is 4 times largerCurrent math used:
My question is: what mathematical way can I use to slow down the growth of a font size given some ratio.
Something like: the higher the 'scale factor', the larger the 'slow down factor'.
As this is for CSS, the only usable math operators are: + - / *
This is the current (pseudo) code (working as expected, btw):
size0 = basesize * a11y-scale
size1 = size0 * scalefactor
size2 = size1 * scalefactor
size3 = size2 * scalefactor
etc...
size-1 = size0 / scalefactor
size-2 = size1 / scalefactor
size-3 = size2 / scalefactor
etc...Combined with a generic document scale factor I will be using this to create a tutorial on how to make a website more accessible (The a11y Project) to the Vision Impaired.
So, much obliged in advance!
#3 Help Me ! » Text on a circular path, how to get minimally required r? » 2021-10-24 10:22:35
- renevanderlende
- Replies: 1
Hi All,
I want to place text on a circular path and need to calculate the minimally required radius (r) so all characters fit exactly on the circle.
height of character: y
width of character: x (variable, but considered equal to y for now)
number of characters: n
degrees per character: 360 / n
I could use r = 2y, but that feels like cheating.
How do I calculate the exact value of r?
Update: I think I found it myself
circle circumfence = 2πr
In my case: minimal circumfence = n * x
radius = circumfence / 2π
So minimally required r = (n*x) / 2π
Would that be correct?
Cheers,
Rene
P.S.: I now know how to use trigonometry functions in CSS, should not pose (much of) a problem.
#4 Re: Help Me ! » How to find Opposite and Adjacent with only Hypotenuse and an Angle? » 2021-10-19 10:36:39
Okay, it all seems to work out as expected...
Thanks Bob, for point me in the right direction!
here you can find a working demo, which still needs some work done as I encountered a several different problems, but I'm pretty pleased with the result thusfar. Simply move the slider and see the CSS trigonomtry and linear math at work.
To web developers: All movement, sizing and scaling is done in CSS only without the use of Media Queries.
The (pseudo) code summary:
Original CSS Trigonometry in CSS by stereokai on Github.
angle = slider value; /* the only action handled by Javascript */
rad = angle * 0.01745329251; /* angle x Pi / 180 */
/* Sine function representation => Math.sin(angle) */
s-term0 = rad;
s-term1 = (-1 / 6) * rad * rad * rad;
s-term2 = ( 1 / 120) * rad * rad * rad * rad * rad;
s-term3 = (-1 / 5040) * rad * rad * rad * rad * rad * rad * rad;
s-term4 = ( 1 / 362880) * rad * rad * rad * rad * rad * rad * rad * rad * rad;
s-term5 = (-1 / 39916800) * rad * rad * rad * rad * rad * rad * rad * rad * rad * rad * rad;
sin = s-term0 + s-term1 + s-term2 + s-term3 + s-term4 + s-term5;
offset = ribbon-width * sin - ribbon-height;
rotate rectangle 'angle' degrees around pivot point => CSS transform: rotate();
move pivot point to 'offset' => CSS top or bottom: offset;
Now, how fun is that?
Rene
#5 Re: Help Me ! » How to find Opposite and Adjacent with only Hypotenuse and an Angle? » 2021-10-17 02:15:43
I approach these kind of problems as a puzzle (like someone else would do Sudoku or Word-Feud). I'm posting this, so others can see how this could be done and to summerize my thoughts...
Here it goes:
Inside a main window ABCD:
I want ribbon GFEC placed in the top (= 0), right (= 0) corner of the webpage,
rotated 30 degrees around point G (transform-origin: bottom right).
- on small displays (320px, mobile) it is width = 180, height = 24
- on large displays (1920px, desktop) it is width = 260, height = 32
- font size = 10 on 320px displays and font size = 16 on 1280px displays
For the above sizes we use the point slope form of y = mx + b, using points (x1,y1)(x2,y2)
- width uses points p1(320,180) and p2(1920,260) => line f
- height uses points p3(320,24) and p4(1920,32) => line e
- font-size uses points p5(320,10) and p6(1280,16) => not mentioned, just here to be complete.
Equation for sizes: y = y1 + (y2 - y1) / (x2 - x1) * (100vmin - x1)
where 100vmin means: 100% of the current viewport minimum(height, width), the variable that does the scaling upon browser resize.
After rotation resulting ribbon position GF'E'C' must be moved down so point F is on line AC (top of main window).
- where top = width * sin(30) - height
As we cannot use CSS attributes 'width' and 'height' in calculations, we need to substitute them with their respective point-slope forms. Something like:
- ribbon top = (y1 + (y2 - y1) / (x2 - x1) * (100vmin - x1)) * sin(30) - (y3 + (y4 - y3) / (x4 - x3) * (100vmin - x3))
As discussed earlier: Trigonometry in CSS
I still need to program this and verify the above logic. Will report back later.
Rene
#6 Re: Help Me ! » How to find Opposite and Adjacent with only Hypotenuse and an Angle? » 2021-10-17 01:10:19
Yep, point F' of GF'E'C' has to end up at line EC.
Now, to position some element in CSS with coordinates is massively counter intuitive. In fact, an element gets moved up/down/left/right by assigning a value to its top/bottom/left/right attributes. This differs from the usual local or world coordinates to position some graphic object.
Furthermore, the top/bottom/left/right attributes of an element are also used to define a size (next to width/height attributes), all depending on the elements' purpose.
While I would highly appreciate an example, unless you know how positioning works in CSS this could become quite messy.
Consider the following:
The large rectangle (browser window, ABCD) is 1920 wide, 1200 tall (my PC display)
And original rectangle (GFEC) is 300x50.
To position GFEC in the top/right corner its attributes would be:
- top: 0
- right: 0
- width: 300
- height: 50
Instead of width: 300 and height: 50
I could have used left: 1620 (being 1920-300) and bottom: 1150 (1200-50).
This is all about CSS 'relative positioning' compared to math/2D/3D 'absolute positioning'.
So, yes please, unless you lack the proper CSS knowledge. I wouldn't want you to lose sleep over this....as you said, my math should work already...
Rene
#7 Re: Help Me ! » How to find Opposite and Adjacent with only Hypotenuse and an Angle? » 2021-10-16 20:50:31
Now that I know that I'm looking for 'CSS trigonometric functions' I learned that CSS will have those functions available in the foreseeable future.
Awaiting those, in the mean time someone else did the hard work and created a 'Trigonometry in CSS - generator' on Codepen, making my life so much easier.
And wadda you know, I can calculate the factorials manually (duh! ...headslapping myself now...) and use those values.
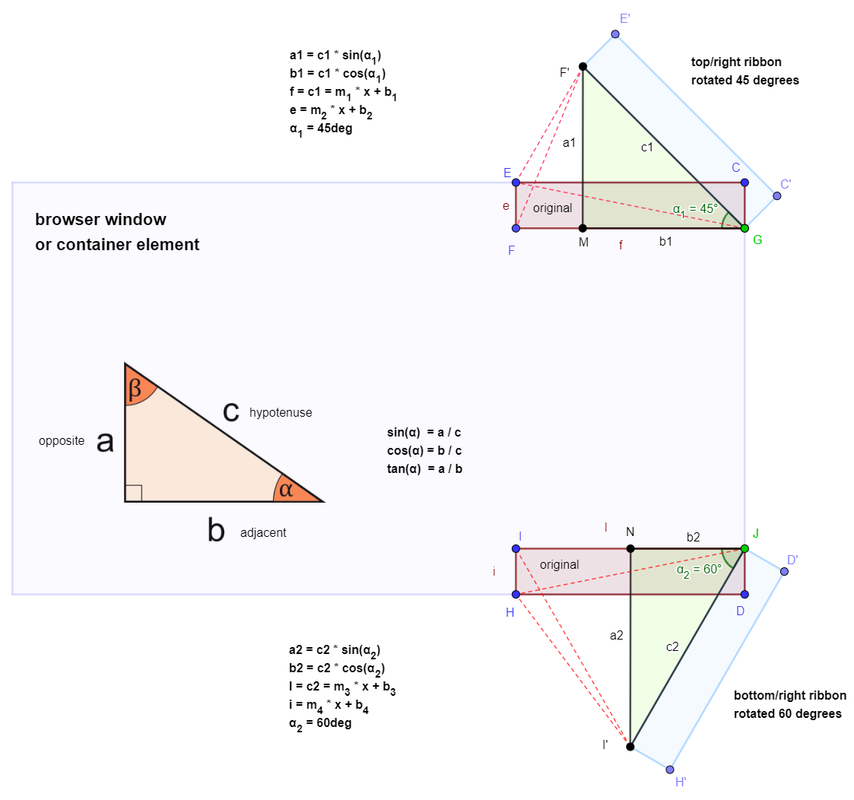
Checking my image above, the final solution would be: movement = hypotenuse * sin(angle) - height of rectangle
(a1 = c1 * sin(angle1) and e = result of y=mx+b => movement = a1 - e)
Is that correct?
Rene
#8 Re: Help Me ! » How to find Opposite and Adjacent with only Hypotenuse and an Angle? » 2021-10-16 11:07:35
Newton already? Go figure...
I went to read the docs you suggested, didn't you hear me scream??
Thanks for your help and insight thusfar, I'll report back in this post as soon I've got something useful to add. Although, I expect not being able to introduce Factorials into CSS, but who knows...
Laterzz!
Rene
#9 Re: Help Me ! » How to find Opposite and Adjacent with only Hypotenuse and an Angle? » 2021-10-16 04:16:13
Now that's a bit of a bummer, to say the least. However, rereading my posts above and checking MathIsFun: 'Finding a Side in a Right-Angled Triangle' I should have known.
Do I read correctly that result = sin(30) is some itterative process? (This put me on the wrong track as I don't supply any triangle leg length values).
Could you please give an example for 'result = sin(30)' (some arbitrary angle) how this would work with the 'power series' you mention?
(or point me to some documention discussing the technique).
As I mentioned wanting to address: for the Square Root the (pseudo) code would be something like:
/*
CSS square root logic with calc() and custom variables
Up to ten guesses to find: result = Sqrt(some value)
The number of required guessed depends on the number of digits
in the none-decimal part of the value we want to Sqrt().
rule of thumb: guesses = number of none-decimal digits * 2 + 1
(...I still need to check whether this is true...)
g1 = (val + val / val) / 2; // guess 1
g2 = (g1 + val / g1) / 2;
g3 = (g2 + val / g2) / 2;
g4 = (g3 + val / g3) / 2;
g5 = (g4 + val / g4) / 2;
g6 = (g5 + val / g5) / 2;
g7 = (g6 + val / g6) / 2;
g8 = (g7 + val / g7) / 2;
g9 = (g8 + val / g8) / 2;
result = (g9 + val / g9) / 2; // guess 10, final result
This does yield proper results after testing...
*/
#10 Re: Help Me ! » How to find Opposite and Adjacent with only Hypotenuse and an Angle? » 2021-10-15 11:28:09
Hi Bob, good to talk to you again! Been well over a year now. Time to do a little math again...
The point is that after rotation (around point G or the other rectangle around point J) most of the rectangle is out of view of the user.
To get it back in view again, it has to be moved down. As you can see from the demo page, in some cases I cut off the corner edges to make it appear tightly fit. The other cases give a more 'sticky tape' feel.
The distance to move down would be length of line a1 minus length of line e (from what I can determine). That way point F' ends up at the long horizontal line (browser window top edge) and point G 'glides' nicely downward along the vertical edge.
I could use trig functions (sqrt, power, sin,cos,tan) using Javascript without problem, but I don't want to. It's a mental 'trying to see how far I can stretch this' thing I have (and CSS vs Javascript coding). Using square root will be the hardest as it is an iterative process in any programming language. I have a solution for that, something I intend to pass you by after this issue.
So, basically the problem is: what is the distance to move down to get point F' on the top edge (and alternatively move point I' up to get it on the lower edge; same math, different signs, other rotation location. The same goes for rectangles on the left side of the screen).
Rene
On a side note: I use the point-slope form of y=mx+b => y = y1 + (y2 - y1) / (x2 - x1) * (x - x1) to calculate both width (line f (or FG)) and height (line e (or EF)) of the rectangle to scale it depending on the size of the browser window.
#11 Help Me ! » How to find Opposite and Adjacent with only Hypotenuse and an Angle? » 2021-10-15 02:36:44
- renevanderlende
- Replies: 13
Hi All!
For a triangle
- AB (opposite)
- BC (adjacent)
- AC (hypotenuse)
I need to find the 'length of AB' given the angle and length of AC without a calculator (no sin/cos/tan functions available!).
- length of AB = a
- length of BC = b
- length of AC = c
The proper formula to find the 'length of AB' would be either a = c * sin(angle) or a = c * cos(90 - angle)
As sin(θ) = Opposite / Hypotenuse
and cos(θ) = Adjacent / Hypotenuse
How do I find the 'length of AB' as neither Opposite nor Adjacent are known?
Bob came up with a perfect solution in a previous discussion, but that only works for an angle of 45 degrees (and a different rotation point E instead of G in the image below).
(Demo page of the solution at work. All rotated elements on that page use the same equation).
However, now the solution has to work for any rotation angle of AC.
To help me figure this out I created a project on GeoGebra (image below).
The image below depicts a browser window (or some container element on a webpage), the large blue rectangle.
- 'original' rectangle ECFG gets rotated 45 degrees around point G to position E'C'F'G (top/right ribbon, rotated 45 degrees).
- from rectangle F'MG you can determine that E'C'F'G has to move down a1 minus e to place it in the corner of the main blue rectangle.
Here's where I get stuck as Opposite (F'M) and Adjacent (MG) are unknown! I added a few optional triangles (dashed lines) that can be used, but I just don't get it....
(bottom/right ribbon, rotated 60 degrees shows the same problem).
To web developers: I need this to be a CSS only solution, using Javascript I would not have this problem, but then it would not be a nice little puzzle to solve...
#12 Re: Computer Math » Programming vs algorithm » 2020-07-01 14:16:43
To understand an automation problem you need to ask many questions (the five Ws) before you can start coding anything. In my IT career I've come to 8:
w8b4udo (wait before you do) who-what-where-when-which-whos-with-why => how
By iterating over those questions, inevitably how to solve the problem will present itself. For IT problems this usually means do some progamming.
Algorithms are a way to solve specific problems programmatically.
#13 Re: Help Me ! » Position a rotated, variable sized rectangle » 2020-04-27 01:08:48
Gloating?? I meant glowing, arghh, NL-EN translations....
#14 Re: Help Me ! » Position a rotated, variable sized rectangle » 2020-04-23 02:13:31
Thanks Bob, I will do that (as soon as I'm finished gloating and padding myself on the back).
But I think I will post a mini tutorial in the 'Coder's Corner', something like 'Why use algebra and trigonometry in CSS' referencing the above. This way I can safely link math to programming (less appropriate here in 'Help me!').
For now
BC = AB.cos(67.5) = 2r.cos(67.5) times cos(67.5)
is what I needed to get a good nights' sleep again!
Final Result, works in all (Windows) browsers (even IE11).
Final code (for IE11 to work properly, ribbon scale = 1.1):
top : calc(((0.5vmin + 1.4rem) * 1.1) / 1.4142 * -1);
right: calc((((0.5vmin + 1.4rem) / 1.4142) + (2 * (5vmin + 10.25rem) * 0.38268343 * 0.38268343)) * 1.1 * -1);
In the mean time I'm considering this topic done and dealt with...
Rene
#15 Re: Help Me ! » Position a rotated, variable sized rectangle » 2020-04-22 13:54:33
Hi Bob,
Awaiting your reply I decided to translate your tut into CSS. And guess what? It worked the first time around!
I am relieved and happy (as a toddler with a new pacifier).
For me distance 3 = 2r.cos(67.5) * cos(67.5) is easy enough to understand, the mathematical logic will take time to sink in, though.
Remember, as I am using rectangles instead of lines, I need to go up distance 1 and go right distance 2 (which both are derived from the height of the rectangle) depicted in the first image I posted. Using your tut and filling in the up and right values, the final (simplified) code looks like this:
- negative because I need to go above the top and beyond the right border
- use a scale factor for the output size of the ribbon
- ribbon height = hm * x + hb
- ribbon width = OA = OB = r = wm * x + wb
- sqrt2 = sqrt(2) = 1.4142...
- cos = cos(67.5) = 0.38268343
- can only use +,-,*,/
top = calc((hm * x + hb) / sqrt2 * scale * -1)
right = calc((((hm * x + hb) / sqrt2) + (2 * (wm * x + wb) * cos * cos)) * scale * -1)
And I didn't even need to use radians...
Now I need to take it up a notch and only work with 45deg, p1(x1,y1) p2(x2,y2) and put the full 'point slope' form into the eqation for both width and height of the rectangle, as well as the equation for cosine. It won't probably even compute (in CSS).
To humour you, the pure CSS (with 'custom variables'), just the parenthesis alone keep me awake at night:
.ribbon {
top : calc(((var(--hm) * var(--x) + var(--hb)) * var(--scale)) / var(--sqrt-2) * -1);
right: calc((((var(--hm) * var(--x) + var(--hb)) / var(--sqrt-2)) + (2 * (var(--wm) * var(--x) + var(--wb)) * var(--cos67dot5) * var(--cos67dot5))) * var(--scale) * -1);
}
Well, as long as it works.
Truly happy about this,
Thanks Bob!!
#16 Re: Help Me ! » Position a rotated, variable sized rectangle » 2020-04-22 03:21:26
Hi Bob,
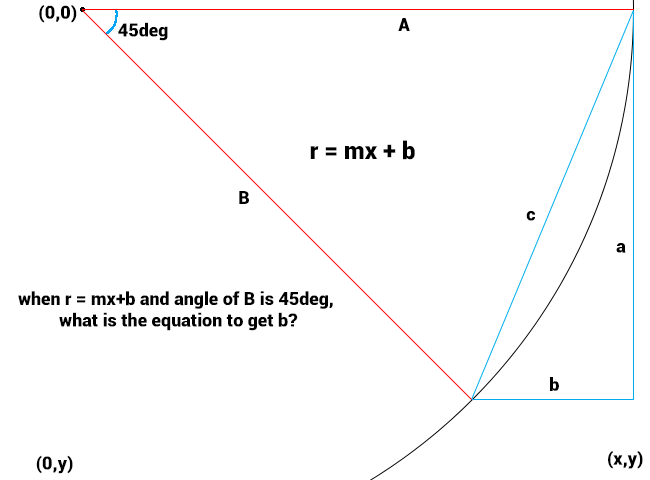
Before anything else, please confirm that the below image depicts your previous explanation before I dive into the math and translate this to something my programmer head comprehends...
As I draw these things with Photoshop, the center of AB = D is a bit by approximation (meant as center, though).
I also adjusted the text a bit '...line d' and 'd' were previously '...line b' and 'b'. Just to prevent confusion with the 'b' in r = mx+b, so you know.
#17 Re: Help Me ! » Position a rotated, variable sized rectangle » 2020-04-21 14:17:41
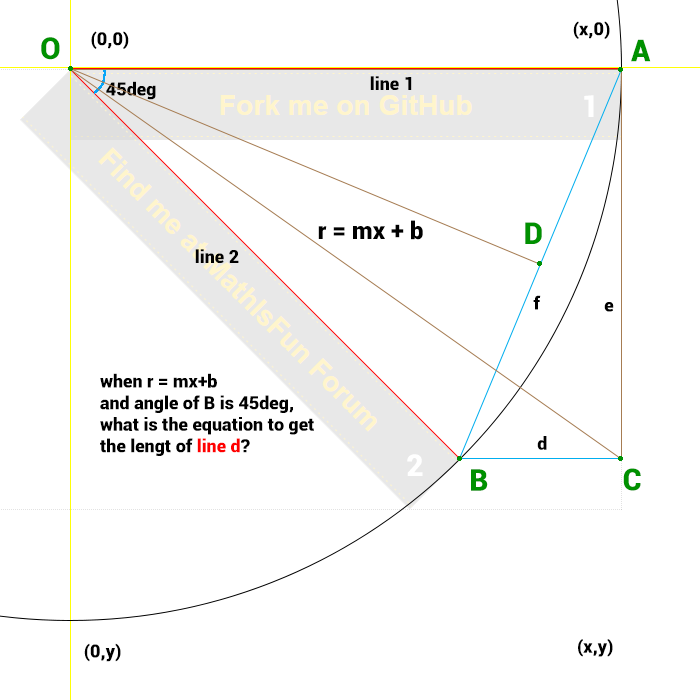
In addition to my previous post, I think I have been able to simplify my problem. Beware though, I am bad at math and while I may literally see a relation with my eyes, I really have no idea if I the below image is algebraicallilly correct.
I drew a circle (center at 0,0) with radius r = mx + b (the width of my ribbon) and a line B of length r (or mx + b) with an angle of 45 degrees. As you can see I (think I can) define a triangle a,b,c and obviously I see Pythagoras making an entrance. I just cannot connect the dots....
What is the algebraic equation for b when I only have (0,0), 45 degrees and y=mx+b to work with? (without using any values, that is)
Yes, I'm aware I should have picked up growing daisies...
#18 Re: Help Me ! » Position a rotated, variable sized rectangle » 2020-04-21 03:09:19
LOL,
I have a habbit of yabbering a lot and saying zilch, sorry for that. Quite some piece of text, though?
- Rectangle(1) is there for reference only, to show the initial location of rectangle(2) before it is rotated 45 degrees. You can safely ignore rectangle(1).
- I did not want to use too much CSS-like syntax and as you asked for values the last time I posted a problem, I tossed in a few I had calculated before.
However....
I think we have a programmer versus mathematician problem, we can read eachothers work, but don't fully speak the same language (I noticed that too during our previous conversation about scaling a text). After 40 years I am so used to thinking like a programmer it is hard not to, I'm sure you have something similar from a math perspective. Or...I am just a nincompoop (really wanted to use that word at least one time in my life!).
I constantly need to remind myself that you are probably not into CSS and therefore I have to translate 'code' to 'math' to explain my problem.
hm * x + hb depicts the height of a ribbon, hm and hb are just names of variables, not h*m and h*b (that's why programmers use names instead of letters only, and they do not automatically put/use a multiplification dot '.' between letters like mathematicians do).
wm * x + wb depicts the width of a ribbon, ditto
So....
x - always given (in CSS: 1vmin, where 'vmin' is a variable unit, which depicts a percentage of the smaller of the current browser viewport width and height. Extra: vw, vh and vmax units depict a percentage of the current browsers' width, height and maximum of the two respectively. So, in this case 1% of the minimumValueOf(viewportWidth,viewportHeight) ).
hm - height m value of the ribbon (in the given example: 0.5)
hb - height b value of the ribbon (= 22.4)
wm - width m value of the ribbon (= 5)
wb - width b value of the ribbon (= 164)
In pseudo CSS...
The below code moves rectangle(2) up and right as shown in image 2 (actual webpage result. Will NOT run properly in Internet Explorer 11. Firefox, Edge and Chrome are okay).
ribbon-values {
/*
Need to be filled in by some programmer as per requirement.
I created an open-source tool to get these values. Like the one in mathportal, but my version returns CSS code.
responsive sizing tool 1.1
Extended version (very WIP) with demos and explanation of the math. Yah, been quite busy this week...
Resize the browser and you will see all kinds of sizing and scaling going on. All linear equations doing that, learned from 'MathIsFun', so, full credit to you guys!!
*/
hm: 0.5;
hb: 22.4;
wm: 5;
wb: 164;
scale: 2.5;
sqrt2: 1.4142;
}
ribbon {
/* showing relevant variables only: */
height: calc((hm * 1vmin + hb) * scale);
width: calc((wm * 1vmin + wb) * scale);
rotate(45deg);
/* distance 1 */
top: calc((hm * 1vmin + hb) / sqrt2 * scale);
/* distance 2 + 3, equation I can't find */
right: ?????
/* currently used for distance 2 + 3, but not correct */
right: calc((wm * 1vmin + wb) / sqrt2 * scale * 0.545)
}
Important to know: opposed to math in CSS location (0,0) is located at top/left instead of bottom/left. But that is usually a matter multiplying the result with -1 (maybe ignore this for now).
As you can see from the actual webpage result I gave mathematically sizing, rotating, and shifting up rectangle(2) all work as expected. All I need now is to get the proper math for shifting it right as distance 2+3 ('right' in CSS) = '(wm * 1vmin + wb) / sqrt2 * scale * 0.545' is only a workaround for the lack thereof.
Maybe it has something to do with multiplying/dividing/converting degrees to radians after the 45deg rotation? I have no clue whatsoever.
Hopefully somewhat less dodgy, but please let me know if there's too much programming going on, in that case I will try my luck elsewhere, no biggy.
Rene
#19 Re: Help Me ! » Find shortest equation to construct y=mx+b » 2020-04-21 00:02:29
Yeah, Bob,
Seeing the formula I had posted I already got the feeling there was little room for improvement.
Thank you however, for confirming as I was not sure. Much appreciated!!
Will visit the suggested pages.
Cheers, Rene
#20 Help Me ! » Find shortest equation to construct y=mx+b » 2020-04-20 01:35:30
- renevanderlende
- Replies: 2
Hi All,
I frequently use linear equation y=mx+b to size objects in online webpages (font size, height, width, spacing, etc.)
This works like a charm and I am very glad I found its explanation on 'MathIsFun' a few years back.
No I am wondering what the shortest equation is to get y when p1(x1,y1) p2(x2,y2) and x are always known.
I am currently using
Is there even a shorter way to get m and b?
#21 Help Me ! » Position a rotated, variable sized rectangle » 2020-04-20 01:06:44
- renevanderlende
- Replies: 10
Hi All,
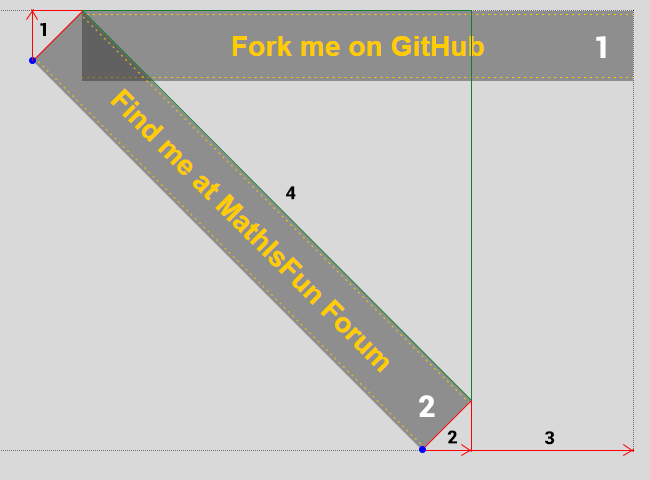
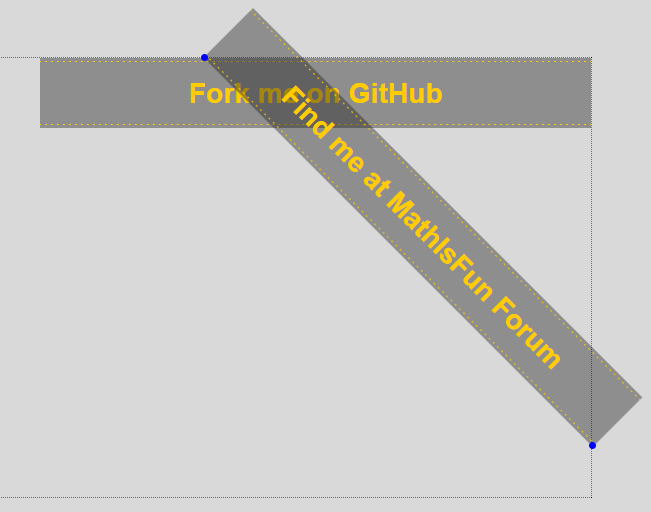
I have a variable sized rectangle, a slanted ribbon, which I want to place in the top/right corner of a webpage.
In the below images I can see what needs to be done (move ribbon distance 1 up and distance 2+3 to the right),
but I cannot find proper equation for distance 2+3.
Could you please help me and show the proper equation for going distance 2+3 right?
Variables:
y = mx + b for
height: points p1(320, 24) p2(1920, 32) => 0.5x + 22.4 => height = hm * x + hb
width: points p1(320,180) p2(1920,260) => 5x + 164 => width = wm * x + wb
rotation: 45 degrees
sqrt2: 1.4142 (to get side of a square from the hypotenuse, 4 significant decimals is more than enough)
scale: 2.5 (in the attached images)
In the below image you can see 2 rectangles (numbers in 'white'),
- one horizontal (1, 'Fork...', used for reference) and
- one slanted (2, 'Find...', which is actually a horizontal rectangle like (1), but rotated 45 degrees around its top/left corner)
- distances (in 'black')
- red and green rectangles to find hypotenuses
- the blue dots are the designated 'bottom/left' and 'bottom/right' corners of rectangle(2)
- the corners depicted by the blue dots need to be placed exactly on the dotted lines (top and right)
Equation for side of a rectangle: side = hypotenuse / sqrt2. Here the hypothenuse is equal to the height of rectangle(2):
- distances 1 (and 2) = (hm * x + hb) / sqrt2 * scale, which I tested and this proved to be correct
- distance 4 = (wm * x + wb) / sqrt2 * scale (not tested, but if the above is correct, then this is too)
- for now, the following equation to move the ribbon right seems to work
distance 2+3 = (wm * x + wb) / sqrt2 * scale * 0.545 (image 2), but does not yield the correct value and is actually cheating as I found 0.545 by trial and error...
Problem:
Final result (manually positioned!):
(You should see 2 images. If not go here examples)
#22 Re: Help Me ! » How to fill a rectangle with N smaller rectangles with given H:W ratio » 2020-03-29 13:04:35
Still being pestered by this thing, ey? Me too.
When the font height is 1 pixel then the 'w' value is the total width of the line of text measured in pixels (in the given example rounded to 150px, virtually unreadable).
The number of characters remains 154 at any given font height.
Should the font size be 6px high, then my assumption is that the the total width of the text will be 6 * 150 = 900 pixels wide.
As it is 6px high, it consumes 6 rows of 1px high and 900px wide = 5400 pixels of the containing box.
Please keep in mind that the font width cannot be chosen or even altered and is font depended. Only the font height can be picked (dropbox in MSPaint, Photoshop, MS Office, browser, etc.).
Also, carefully note the fact that the values of the MSPaint 'W' you counted (20 high and 28 wide) are misleading as paint programs will only draw the actual pixels used for that character, not like a browser does. Here's a little test, select the next few characters and you will see that they all equal in height: WWWwww...xxxXXX,,,oooiiiIII. That's the height we are looking for.
Answering your question on MSPaint: I believe it does not wrap text, so if the font-size you select is to large, it simply gets clipped or runs off the right side of your image.
As said before, the character width can only be measured/determined/derived from the total width of the text in pixels
by using character count as divisor => total text width (in pixels) divided by character count = average character width in pixels (to be complete: at a given font size (= height) in pixels).
summary:
character height in px = required result, value for CSS 'font-size'.
total text width in px = measurable, will give total length of the text in pixels.
character count = measurable, will include any character including hard/soft line or word breaks or hyphens.
character width = not selectable, not given, not available and immutable and can only be derived by measuring and averaging.
A problem that lies ahead is the fact that the text automatically wraps given the word lengths and the width of the container it is put into.
Another problem is what to do when the width in pixels of a single word is wider than the width of the box.
And I purposely left out 'line-height' (by default 1.25 * 'font-size', but can be changed by developers as required, often changed to 1.3 or 1.5). Probably the value we actually need to use instead of 'font-size'.
Also left out 'word-spacing' and 'letter-spacing', good for a massive programmers' headache...
But those are to lie awake over later. First the initial math needs to be correct.
BTW: version 2.2 shows values and usage of the eqations you gave in post #11.
If you are up to it, you can open your browsers' developer tools (usually [F12]): select the 'inspector tab', look at the 'properties window' and select 'calculated'. It will show all the current values of the selected element you see on your screen. You can actually change values and see the effect, (not harmfull, when you mess up, just close and reopen the webpage you were on). Works on most webpages and gives much insight on how things are done.
UPDATE Or [right-click] on anything on a webpage and select 'inspect element', this will open the the developer tools 'inspector tab' with that specific webpage element pre-selected.
MAYBE ill-advised if you are not into web developement and have never seen the window, you may find yourself caught in a snake pit.
René
#23 Re: Help Me ! » How to fill a rectangle with N smaller rectangles with given H:W ratio » 2020-03-29 03:46:47
hi
(arghhh, of course the multiplification are wrong when you have to read them like that).
Actually, once you know, it is quite simple
In JS you can measure the length of a piece of text, provided it has assigned 'font-family' and 'font-size' values. The returned value is a total width value in pixels (most common unit in HTML/CSS).
As I don't have a 'font-size' (read font height), but 'font-family' only ('monospace'), I simply assign a value of 1px as 'font-size'.
In the given example measuring the 'lorem ipsum' text (number of characters = 154) with 'font-size' = 1px and 'font-family' = 'monospace' yields a total width (in pixels) of 150 pixels (rounded for simplicity).
a line of text of 1px high is 150px wide, it consumes 1 pixel row of 1 * the initial width or 1 * 1 * 150 = 150 pixels
a line of text of 2px high is 2 * 150px wide, it consumes 2 pixel rows of 2 * the initial width or 2 * 2 * 150 = 600 pixels (indeed), but 300 pixels per row (that is where I explained it wrong)
a line of text of 3px high is 3 * 150px wide, it consumes 3 pixel rows of 3 * the initial width or 3 * 3 * 150 = 1350 pixels, but 450 pixels per row
My math knowledge and NL-EN translation fail a bit, but that is proportional, linear, I dunno.
So a row of [x] pixels high is [x] * [width] pixels wide. As the box is [Side] * [Side] (square), or [Width] * [Height] (rectangle)
my initial equation for a square box becomes:
or
which leads to
A rectangular box would yield
leading to
The wrapping of the text is automatic, I have no say in that. Given that info, I might just as well treat the containing box as a long strip of pixels (200 * 200 = 40000px) and calculate how often the text of 150px wide fits in the 40000px box. Of course taking into account that I cannot just divide 40000 by 150 = 266.67. That would lead to one row with very small text and 265.67 empty rows.
For ease of testing I curently only use
BUT, while this seems to work out fine, some of the resulting boxes DO fail: 'lorem ipsum....' (too small), 'W W W W W W W W W' (both too small), '123456789' (too wide), '123456789....' (too small).
So, my teeth are getting shorter and shorter from grinding...
While you let this sink in, I'll check the artwork in your post.
#24 Re: Help Me ! » How to fill a rectangle with N smaller rectangles with given H:W ratio » 2020-03-28 23:03:19
Going bananas, right? Well, check youtube for 'The Joy of Painting' with Bob Ross. This guy shows a simple painting technique for creating panoramas, currently also on Spike TV. Very popular back in the day. He never made mistakes, but had 'happy little accidents'. You don't have to like what he does, but his velvet voice is soooo soothing, after 2 episodes you will be more relaxed than you would be after a week of meditation.
Or asleep...
#25 Re: Help Me ! » How to fill a rectangle with N smaller rectangles with given H:W ratio » 2020-03-28 22:38:59
Ok, well, thank you for my servicve then? ![]()
I believe I tried to explain that math in post #8:
As I didn't know an initial font height I simply tried 'growing' one until there would be no more space to spare in the box. After 3 tries I saw the rythm (talking about pixels):
if a string of 1px high is 150px long (1*1*150)
then a string of 2px is 300px long (2*2*150)
then a string of 3px is 450px long (3*3*150, etc)
or fontHeight^2 * stringWidth = boxWidth * boxHeight
=> fontHeight^2 = boxWidth * boxHeight / stringWidth
=> fontHeight = sqrt(boxWidth * boxHeight / stringWidth)
Hence the square root...
Is this correct, or just a happy accident? (Bob Ross fan)
And, I think this still applies in case of a rectangle instead of a square....