Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#1 2021-10-15 02:36:44
- renevanderlende
- Member
- From: The Netherlands
- Registered: 2020-01-06
- Posts: 39
How to find Opposite and Adjacent with only Hypotenuse and an Angle?
Hi All!
For a triangle
- AB (opposite)
- BC (adjacent)
- AC (hypotenuse)
I need to find the 'length of AB' given the angle and length of AC without a calculator (no sin/cos/tan functions available!).
- length of AB = a
- length of BC = b
- length of AC = c
The proper formula to find the 'length of AB' would be either a = c * sin(angle) or a = c * cos(90 - angle)
As sin(θ) = Opposite / Hypotenuse
and cos(θ) = Adjacent / Hypotenuse
How do I find the 'length of AB' as neither Opposite nor Adjacent are known?
Bob came up with a perfect solution in a previous discussion, but that only works for an angle of 45 degrees (and a different rotation point E instead of G in the image below).
(Demo page of the solution at work. All rotated elements on that page use the same equation).
However, now the solution has to work for any rotation angle of AC.
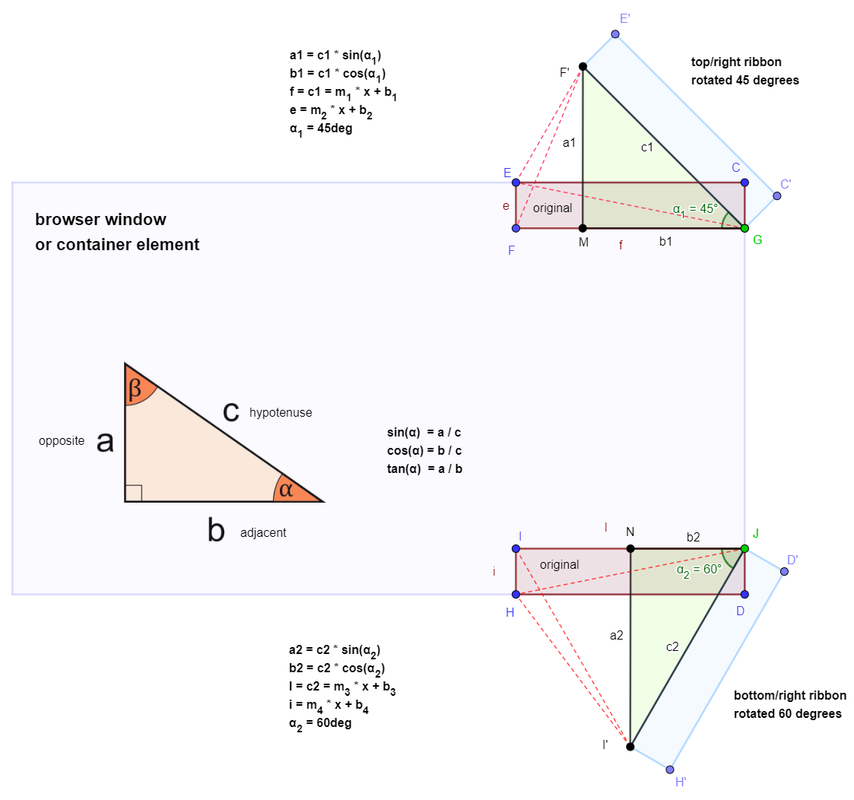
To help me figure this out I created a project on GeoGebra (image below).
The image below depicts a browser window (or some container element on a webpage), the large blue rectangle.
- 'original' rectangle ECFG gets rotated 45 degrees around point G to position E'C'F'G (top/right ribbon, rotated 45 degrees).
- from rectangle F'MG you can determine that E'C'F'G has to move down a1 minus e to place it in the corner of the main blue rectangle.
Here's where I get stuck as Opposite (F'M) and Adjacent (MG) are unknown! I added a few optional triangles (dashed lines) that can be used, but I just don't get it....
(bottom/right ribbon, rotated 60 degrees shows the same problem).
To web developers: I need this to be a CSS only solution, using Javascript I would not have this problem, but then it would not be a nice little puzzle to solve...
Last edited by renevanderlende (2021-10-15 02:44:53)
Offline
#2 2021-10-15 10:03:44
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: How to find Opposite and Adjacent with only Hypotenuse and an Angle?
hi renevanderlende,
Great to hear from you again. Let's see if I've understood the problem.
You have a rectangle that you want to rotate through angle θ about one of the corners, let's say corner X. Before the rotation XY is horizontal. After the rotation you want to know how far Y has moved horizontally and vertically. You cannot use trig functions. Is that correct?
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#3 2021-10-15 11:28:09
- renevanderlende
- Member
- From: The Netherlands
- Registered: 2020-01-06
- Posts: 39
Re: How to find Opposite and Adjacent with only Hypotenuse and an Angle?
Hi Bob, good to talk to you again! Been well over a year now. Time to do a little math again...
The point is that after rotation (around point G or the other rectangle around point J) most of the rectangle is out of view of the user.
To get it back in view again, it has to be moved down. As you can see from the demo page, in some cases I cut off the corner edges to make it appear tightly fit. The other cases give a more 'sticky tape' feel.
The distance to move down would be length of line a1 minus length of line e (from what I can determine). That way point F' ends up at the long horizontal line (browser window top edge) and point G 'glides' nicely downward along the vertical edge.
I could use trig functions (sqrt, power, sin,cos,tan) using Javascript without problem, but I don't want to. It's a mental 'trying to see how far I can stretch this' thing I have (and CSS vs Javascript coding). Using square root will be the hardest as it is an iterative process in any programming language. I have a solution for that, something I intend to pass you by after this issue.
So, basically the problem is: what is the distance to move down to get point F' on the top edge (and alternatively move point I' up to get it on the lower edge; same math, different signs, other rotation location. The same goes for rectangles on the left side of the screen).
Rene
On a side note: I use the point-slope form of y=mx+b => y = y1 + (y2 - y1) / (x2 - x1) * (x - x1) to calculate both width (line f (or FG)) and height (line e (or EF)) of the rectangle to scale it depending on the size of the browser window.
Last edited by renevanderlende (2021-10-15 12:09:11)
Offline
#4 2021-10-16 00:19:19
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: How to find Opposite and Adjacent with only Hypotenuse and an Angle?
hi Rene,
My short response is I cannot do what you want and don't think it is possible.
Back in my youth we used look up tables to do calculations involving sines and cosines. Nowadays, we use scientific calculators. The underlying mathematics for how this works is by the use of 'power series'. Any sine values can be calculated by adding up terms in an infinite series. The terms gradually get smaller so, once you achieve a consistent result to a number of decimal places, the summation can stop as no further improvement in accuracy will result.
css does not have either a look up feature nor a power series routine. It is expected the programmer will use Java or another language.
If two triangles are similar ( have the same angles ) you can calculate additional lengths in one provided you have some lengths in the other. This doesn't seem to be the case here.
If you limited yourself to certain angles only, then it is possible a solution exists, but I think you want a solution that works at run time and for any angle and that's asking far more from css than its designers built in.
Sorry.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#5 2021-10-16 04:16:13
- renevanderlende
- Member
- From: The Netherlands
- Registered: 2020-01-06
- Posts: 39
Re: How to find Opposite and Adjacent with only Hypotenuse and an Angle?
Now that's a bit of a bummer, to say the least. However, rereading my posts above and checking MathIsFun: 'Finding a Side in a Right-Angled Triangle' I should have known.
Do I read correctly that result = sin(30) is some itterative process? (This put me on the wrong track as I don't supply any triangle leg length values).
Could you please give an example for 'result = sin(30)' (some arbitrary angle) how this would work with the 'power series' you mention?
(or point me to some documention discussing the technique).
As I mentioned wanting to address: for the Square Root the (pseudo) code would be something like:
/*
CSS square root logic with calc() and custom variables
Up to ten guesses to find: result = Sqrt(some value)
The number of required guessed depends on the number of digits
in the none-decimal part of the value we want to Sqrt().
rule of thumb: guesses = number of none-decimal digits * 2 + 1
(...I still need to check whether this is true...)
g1 = (val + val / val) / 2; // guess 1
g2 = (g1 + val / g1) / 2;
g3 = (g2 + val / g2) / 2;
g4 = (g3 + val / g3) / 2;
g5 = (g4 + val / g4) / 2;
g6 = (g5 + val / g5) / 2;
g7 = (g6 + val / g6) / 2;
g8 = (g7 + val / g7) / 2;
g9 = (g8 + val / g8) / 2;
result = (g9 + val / g9) / 2; // guess 10, final result
This does yield proper results after testing...
*/
Offline
#6 2021-10-16 08:12:39
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: How to find Opposite and Adjacent with only Hypotenuse and an Angle?
That routine for finding a square root was devised by Newton. My first calculator had only +,- x and divide plus one memory and I used to work out square roots that way in about 30 seconds.
You will find the series expansion here https://www.mathsisfun.com/algebra/taylor-series.html
x has to be in radians not degrees.
There is also a Wiki page that gives the degrees version as well https://en.wikipedia.org/wiki/Sine#Series_definition
You'll have to scroll down to the series definition section.
If you can set that up in css then we have a way forward. Once you have values for cos and sine there's a relatively simple calculation using +, - and x only to get the coordinates of any rotated point around (0,0), so we'd have to set up the right axes system.
I'll stay subscribed to your thread in the hope you can manage it ![]()
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#7 2021-10-16 11:07:35
- renevanderlende
- Member
- From: The Netherlands
- Registered: 2020-01-06
- Posts: 39
Re: How to find Opposite and Adjacent with only Hypotenuse and an Angle?
Newton already? Go figure...
I went to read the docs you suggested, didn't you hear me scream??
Thanks for your help and insight thusfar, I'll report back in this post as soon I've got something useful to add. Although, I expect not being able to introduce Factorials into CSS, but who knows...
Laterzz!
Rene
Offline
#8 2021-10-16 19:45:11
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: How to find Opposite and Adjacent with only Hypotenuse and an Angle?
In your square root routine each g depends on the one before. A similar approach can be used for factorials.
f1 = 1
f2 = f1 x 2
f3 = f2 x 3
and so on.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#9 2021-10-16 20:50:31
- renevanderlende
- Member
- From: The Netherlands
- Registered: 2020-01-06
- Posts: 39
Re: How to find Opposite and Adjacent with only Hypotenuse and an Angle?
Now that I know that I'm looking for 'CSS trigonometric functions' I learned that CSS will have those functions available in the foreseeable future.
Awaiting those, in the mean time someone else did the hard work and created a 'Trigonometry in CSS - generator' on Codepen, making my life so much easier.
And wadda you know, I can calculate the factorials manually (duh! ...headslapping myself now...) and use those values.
Checking my image above, the final solution would be: movement = hypotenuse * sin(angle) - height of rectangle
(a1 = c1 * sin(angle1) and e = result of y=mx+b => movement = a1 - e)
Is that correct?
Rene
Offline
#10 2021-10-17 00:10:21
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: How to find Opposite and Adjacent with only Hypotenuse and an Angle?
hi Rene,
Now you have asked that question you have made me realise that I still don't know precisely what you are trying to do.
Your diagram shows a rectangle GFEC rotating around point G to a new position GF'E'C'
Is that where you want the rectangle to end up? Because a1 - e seems to suggest that after the rotation you are moving the new rectangle down so that F' moves onto the line EC (point not yet labelled).
If so, then your algebra is correct. Please make clear where the 'final resting' place of the rectangle is required to be.
If GFEC has coordinates (0,0) (f,0) (f,c) and (0,c) ** then I can supply a formula that will allow you to calculate the coordinates of F' E' and C'.
** I'm taking the positive x direction to the left.
Would that be helpful?
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#11 2021-10-17 01:10:19
- renevanderlende
- Member
- From: The Netherlands
- Registered: 2020-01-06
- Posts: 39
Re: How to find Opposite and Adjacent with only Hypotenuse and an Angle?
Yep, point F' of GF'E'C' has to end up at line EC.
Now, to position some element in CSS with coordinates is massively counter intuitive. In fact, an element gets moved up/down/left/right by assigning a value to its top/bottom/left/right attributes. This differs from the usual local or world coordinates to position some graphic object.
Furthermore, the top/bottom/left/right attributes of an element are also used to define a size (next to width/height attributes), all depending on the elements' purpose.
While I would highly appreciate an example, unless you know how positioning works in CSS this could become quite messy.
Consider the following:
The large rectangle (browser window, ABCD) is 1920 wide, 1200 tall (my PC display)
And original rectangle (GFEC) is 300x50.
To position GFEC in the top/right corner its attributes would be:
- top: 0
- right: 0
- width: 300
- height: 50
Instead of width: 300 and height: 50
I could have used left: 1620 (being 1920-300) and bottom: 1150 (1200-50).
This is all about CSS 'relative positioning' compared to math/2D/3D 'absolute positioning'.
So, yes please, unless you lack the proper CSS knowledge. I wouldn't want you to lose sleep over this....as you said, my math should work already...
Rene
Last edited by renevanderlende (2021-10-17 01:11:34)
Offline
#12 2021-10-17 02:15:43
- renevanderlende
- Member
- From: The Netherlands
- Registered: 2020-01-06
- Posts: 39
Re: How to find Opposite and Adjacent with only Hypotenuse and an Angle?
I approach these kind of problems as a puzzle (like someone else would do Sudoku or Word-Feud). I'm posting this, so others can see how this could be done and to summerize my thoughts...
Here it goes:
Inside a main window ABCD:
I want ribbon GFEC placed in the top (= 0), right (= 0) corner of the webpage,
rotated 30 degrees around point G (transform-origin: bottom right).
- on small displays (320px, mobile) it is width = 180, height = 24
- on large displays (1920px, desktop) it is width = 260, height = 32
- font size = 10 on 320px displays and font size = 16 on 1280px displays
For the above sizes we use the point slope form of y = mx + b, using points (x1,y1)(x2,y2)
- width uses points p1(320,180) and p2(1920,260) => line f
- height uses points p3(320,24) and p4(1920,32) => line e
- font-size uses points p5(320,10) and p6(1280,16) => not mentioned, just here to be complete.
Equation for sizes: y = y1 + (y2 - y1) / (x2 - x1) * (100vmin - x1)
where 100vmin means: 100% of the current viewport minimum(height, width), the variable that does the scaling upon browser resize.
After rotation resulting ribbon position GF'E'C' must be moved down so point F is on line AC (top of main window).
- where top = width * sin(30) - height
As we cannot use CSS attributes 'width' and 'height' in calculations, we need to substitute them with their respective point-slope forms. Something like:
- ribbon top = (y1 + (y2 - y1) / (x2 - x1) * (100vmin - x1)) * sin(30) - (y3 + (y4 - y3) / (x4 - x3) * (100vmin - x3))
As discussed earlier: Trigonometry in CSS
I still need to program this and verify the above logic. Will report back later.
Rene
Offline
#13 2021-10-19 10:36:39
- renevanderlende
- Member
- From: The Netherlands
- Registered: 2020-01-06
- Posts: 39
Re: How to find Opposite and Adjacent with only Hypotenuse and an Angle?
Okay, it all seems to work out as expected...
Thanks Bob, for point me in the right direction!
here you can find a working demo, which still needs some work done as I encountered a several different problems, but I'm pretty pleased with the result thusfar. Simply move the slider and see the CSS trigonomtry and linear math at work.
To web developers: All movement, sizing and scaling is done in CSS only without the use of Media Queries.
The (pseudo) code summary:
Original CSS Trigonometry in CSS by stereokai on Github.
angle = slider value; /* the only action handled by Javascript */
rad = angle * 0.01745329251; /* angle x Pi / 180 */
/* Sine function representation => Math.sin(angle) */
s-term0 = rad;
s-term1 = (-1 / 6) * rad * rad * rad;
s-term2 = ( 1 / 120) * rad * rad * rad * rad * rad;
s-term3 = (-1 / 5040) * rad * rad * rad * rad * rad * rad * rad;
s-term4 = ( 1 / 362880) * rad * rad * rad * rad * rad * rad * rad * rad * rad;
s-term5 = (-1 / 39916800) * rad * rad * rad * rad * rad * rad * rad * rad * rad * rad * rad;
sin = s-term0 + s-term1 + s-term2 + s-term3 + s-term4 + s-term5;
offset = ribbon-width * sin - ribbon-height;
rotate rectangle 'angle' degrees around pivot point => CSS transform: rotate();
move pivot point to 'offset' => CSS top or bottom: offset;
Now, how fun is that?
Rene
Offline
#14 2021-10-19 19:13:13
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: How to find Opposite and Adjacent with only Hypotenuse and an Angle?
hi Rene,
Well done. Glad you are making progress.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline