Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#1 Re: Exercises » Bitter areas. » 2025-12-14 00:03:45
Hi Bob;
I've checked all my posts and I'm blocked from viewing every Imgur image!..........I haven't had a chance to check yet, but as I read it, I won't be able to log in to Imgur either.
From Reddit.com's Imgur blocks access to UK users after proposed regulatory fine:
A help article on Imgur's US website, seen by the BBC, states that "from September 30, 2025, access to Imgur from the United Kingdom is no longer available".
"UK users will not be able to log in, view content, or upload images. Imgur content embedded on third-party sites will not display for UK users."
What site are you now using?
https://postimages.org/, and so far, so good (well, nearly). Some points:
1. Registering enables using galleries.
2. Their hotlinks don't include a BBCode img-tag option. Best options:
(a) 'Direct link' is missing the img tags...so enter them manually.
(b) 'Hotlink for forums' includes the img tags, but also url tags...so delete them manually.
3. Image resizing is possible (but limited), and must be done before upload (Imgur's is after upload, making results easier/faster to analyse). Also, their resize compression spoils the image somewhat, and so I pre-sized the post #19 images with IrfanView (my image viewer) for better quality.
And how long before that bans the UK too.
I'm now very happy that I have originals of all my Imgur images in a folder (have done similar for Postimages). That way, my images are always available for alternative file host solutions, should the need arise.
#2 Re: Exercises » Bitter areas. » 2025-12-13 00:27:23
Hi Bob;
I started using Imgur in late Feb 2017, and have 304 images stored there.
Most of them are on MIF posts, and, from what you've found and from what's reported on Reddit and elsewhere about Imgur's UK ban, they're probably all now invisible to UK members.
I did some testing down here via a VPN set to several different UK locations, but that failed as all my images (over a large range of dates) remained visible to me.
Maybe I'll cherry-pick a post or three to 'fix' my invisible images for UK-ians by changing them over to a non-Imgur file host...like I've done in this thread.
I wonder if Imgur's UK ban is permanent?
Of course, while the ban is in place, I won't be using Imgur for a global audience.
![]()
#3 Re: Exercises » Bitter areas. » 2025-12-11 11:32:39
Hi Bob,
I'm getting a 'Content Not Viewable In Your Region' message instead of your Imgur images. Any idea why that is happening?
Yes...but only after googling it a few moments ago.
From Reddit.com: Imgur blocks access to UK users after proposed regulatory fine.
Not sure exactly what to do about that from down here, but Reddit gives some suggestions for UK-ians: Imgur alternatives for UK users.
Well...that's all VERRRRRRY annoying!!!!!! ![]()
EDIT: I'm trying another file host: https://postimages.org/, and have changed the images in this thread over to them. Do my images show up for you now? There are 5 in post #19, 1 in post #18, & 1 hidden one in post #4.
#4 Re: Exercises » Bitter areas. » 2025-12-10 21:23:28
Hi mycalsuite;
The three internal-point-to-vertex lengths are often a Pythagorean triple (bobbym's {500,1200,1300} is one), opening up the use of a particular solution strategy.
Here's a geometric solution...
1. Draw large △ABC, consisting of 3 smaller coloured triangles △BAD, △CBD & △ACD that connect to inner point D where the explosion occurred.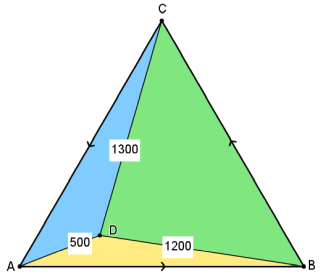
2. (a) Rotate the 3 coloured triangles 60° clockwise:
(i) the gold around point B, producing point E and forming the 60° ∠EBD.
(ii) the green around point C, producing point G and forming the 60° ∠GCD.
(iii) the blue around point A, producing point F and forming the 60° ∠FAD.
(b) These rotations together form outer hexagon AFBECG, whose total area is exactly twice that of △ABC.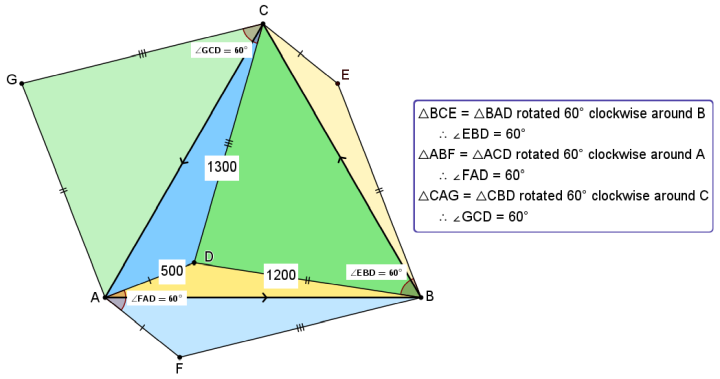
3. Draw lines DE, DG & DF to complete triangles △DBE, △DCG & △DAF, respectively.
(a) These 3 triangles are equilateral as they're isosceles with a 60° included angle at B, C & A, respectively.
(b) The remaining regions of the hexagon — the 3 triangles △DEC, △BDF & △GAD — are congruent right-angled triangles, each with sides {500,1200,1300} — a Pythagorean triple.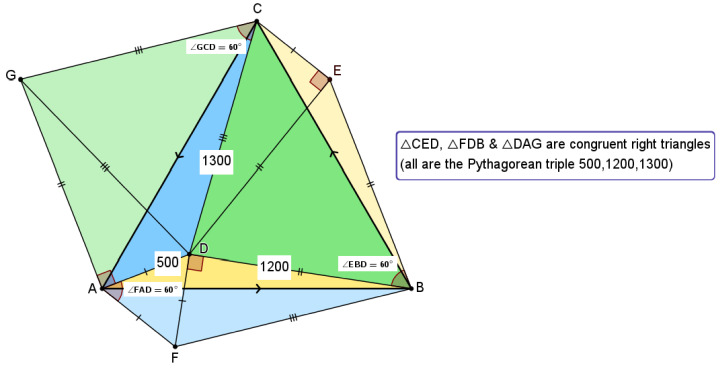
4. The area of the hexagon is the sum of:
(a) the areas of its 3 equilateral triangles, and
(b) the areas of its 3 congruent right-angled triangles.
5. The area of △ABC = ½hexagon = 2500(180+169√3) ≈ 1181791.46619785.

#5 Re: Exercises » Bitter areas. » 2025-10-22 00:53:19
Hi mycalsuite;
A is right; there isn't enough data to identify the area in a unique way.
The equilateral triangle's size is not uniquely fixed by the distances to its three vertices.
As a result, the area cannot be calculated using the information provided.
By "not uniquely fixed", do you mean that multiple solutions are possible?
If so, do you have an example you could post?
Bobbym (OP), thickhead, ElainaVW and I have all arrived at the same single solution (ElainaVW's 2500√3(169+60√3) being slightly less simplified than the others' 2500(180+169√3).
Here's the Geogebra drawing I mentioned in post #4:
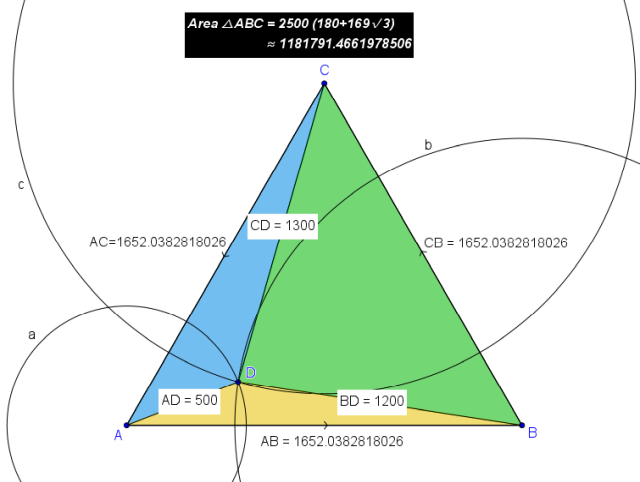
The Geogebra measurements check out...
EDIT: I googled this puzzle yesterday, and found that it has appeared in different guises over many years (more recently on websites such as Artofproblemsolving, math.Stackexchange and Reddit). The three internal-point-to-vertex lengths are often a Pythagorean triple (bobbym's {500, 1200, 1300} is one), opening up the use of a particular solution strategy. All solutions I found are single.
#6 Exercises » Applied Maths: Find base cost, given nett after levies & commission » 2025-10-18 21:42:27
- phrontister
- Replies: 0
The nett cost (N) of a property's fire insurance policy comprises the following components:
P = Premium (the base cost)
F = Fire Services Levy (f% of the Premium)
S = Stamp Duty (s% of the combined Premium & Fire Services Levy)
C = Commission (c% of the Premium)
And N = P + F + S - C.
A policyholder pays $1224.81 nett (N), where...
f = 2.5%
s = 11%
c = 15%
Q1. What is the amount of the policy's Premium (P) component (ie, the base cost)?
Q2. What's the shortest algebraic formula you can make to solve Q1?
Note: The formula must include rate variables f, s & c.
#7 Re: Help Me ! » Problem of permutation and combination » 2025-10-03 16:05:20
Hi Bob;
That makes 10 ways.
Isn't each of your 20 lines a distinct permutation, making 20 ways?
If so, that yields 20 * 3 = 60...and 60 + 90 = 150.
#8 Re: Help Me ! » Inserting an image -- ? » 2025-09-25 14:47:58
Hi all;
I've updated a couple of steps in the post #4 that I referred to in my previous post.
The main change is to Step 5, which is now "Long-press the image, & select 'View image' ".
It previously said to select 'Review image', which I recently found doesn't always appear in the drop-down menu from the long-press. 'View image' does (at least it did in all my tests, which were quite a few).
The change to Step 5 then led to a change in Step 6, which is now simpler.
I hope the step sequence works on phones other than mine! ![]()
#9 Re: Help Me ! » Inserting an image -- ? » 2025-09-19 18:03:40
#10 Re: Help Me ! » Image test 2 » 2025-09-19 17:30:56
Hi Bob;
Yay! I've done this totally on my phone.
Me too! ![]()

The image is of the North Sydney Olympic Pool & the nearby Sydney Harbour Bridge on a nice, clear day, compared to what they looked like during the enormous Eastern Australian red dust storm in September 2009.
Here's the code I used to display the image:
[img]https://i.imgur.com/Z0HakbV.jpeg[/img]BTW, I uploaded my image to Imgur, and obtained their image link (minus the BBCode image tags), without logging in to Imgur.
The steps in my Samsung Galaxy A35:
1. Go to Imgur.com
2. Press the Upload button (an arrow pointing up from a flat tray).
3. Select the image from its location on your phone (eg, Gallery).
4. Press 'Done', & wait until both the image & 'Upload Complete!' display.
5. Long-press the image, & select 'View image'.
6. Press the address in the address bar (it will change to a highlighted url of the image file).
7. Press the 'Copy' button immediately right of the file url ('Copied to clipboard.' will then display lower down the page).
8. Paste the copied file url into your MIF post, inside BBCode square image tags (like in the code shown above).
No doubt the steps are phone-dependent (or some such)! ![]()
#11 Re: Help Me ! » Surds » 2025-07-22 16:50:58
Hi Paul;
First off, sorry for the giant image
I resized it in Windows but it kept coming out huge
I don't know the reason for that happening here on MIF ![]() , but this is what I do to get the approx size I want for my display:
, but this is what I do to get the approx size I want for my display:
1. Crop out what I don't need displayed (using M$ Paint, or some such). Cropping your image reduced it from 800px x 1778px to 743px x 530px, which removed about 72% of the original area!
2. Upload the cropped version to Imgur.
3. Enter Imgur's BBCode image link into my MIF post, and before pressing Submit, click Preview to assess image size.
4. If I want to change the image size, then immediately before the full stop of the image extension (eg, .jpeg, .png) I insert one of the following letters:
s (Small square)
b (Big square)
t (Small thumbnail)
m (Medium thumbnail)
l (Large thumbnail)
h (Huge thumbnail)
I copied your image, cropped it, and uploaded it to my Imgur.
To resize that image from original to medium, its original link https://i.imgur.com/8adTo66.jpg would become https://i.imgur.com/8adTo66m.jpg (note the inserted 'm' before the extension's full stop).
Here's the cropped image at original size: 
And here's the image shrunk to medium size:
And here are the displays for all 7 size options (including the original) based on the cropped rectangular image I uploaded to Imgur:
You'll notice that the left and right sides of the 'small square' and 'big square' images are cropped. Unfortunately, Imgur does that automatically on rectangular images whose width exceeds their height, so if such cropping matters, either:
(a) don't use the 'small square' or 'big square' options on the rectangular image, or
(b) convert the rectangular image to a square (eg, by adding false top &/or bottom with image software).
Is using imgur.com a good way to post images here?
Is there a better alternative?
I've used Imgur since 2017, and think it gives a very good file host service.
They've changed their webpage layout to a somewhat confusing one that I haven't totally sussed out, but (lucky for me) on one of their pages (I forget which one) they give an option to use their old style...which I select straight away!
I don't know of a better alternative file host.
I use a PC &/or laptop. I've only had a 'smart'phone for a few months and am still learning it, so if you're on one of those things and have Qs about what I've said, we may need someone else (Bob?) to help out. ![]()
#12 Re: Puzzles and Games » Add 13 more and post it forever. » 2025-04-27 03:04:58
30225
#13 Re: Help Me ! » Can u find the word? » 2025-04-03 11:09:59
Hi punhub85;
Any chance there's a word that has a, e, i, o, u, y in order?
Yes...the adverbial forms of the two adjectives you mentioned ('facecious' & 'abstemious') fit: 'faceciously' & 'abstemiously'.
For hyphenated words, there's also the adverb 'half-seriously' (from the adjective 'half-serious').
Collins Dictionary (a British dictionary) has 'halfseriously' but not 'halfserious', only the hyphenated 'half-serious'! ![]()
The unhyphenated 'halfseriously' is valid in Scrabble games where British words are used.
#14 Re: Help Me ! » Dinner puzzle....Please help! » 2025-02-28 01:18:56
Hi Kerim;
Isn’t it a solution?
Well, not really, unless the "I would like" in Nick's "I would like everyone to meet at least once" is only a desire, not a requirement.
01 doesn't meet 08, 15 & 22
08 doesn't meet 01, 15 & 22
15 doesn't meet 01, 08 & 22
22 doesn't meet 01, 08 & 15
02 doesn't meet 09, 16 & 22
09 doesn't meet 02, 16 & 22
etc, etc.
Ditto for 01, 08, 15 & 22 in your post #16.
Also, in post #16, guest 02 only meets 01, 03, 04, 05, 06, 07, 08, 15 & 22, and fails to meet any of the other 18 guests.
Just looking quickly, 03 does much the same as 02.
I didn't check further...
#15 Re: Help Me ! » Dinner puzzle....Please help! » 2025-02-26 03:12:41
I've done the following in Excel (spreadsheet...by hand, coz I don't know how to code progressive dinners): 
Guests are numbered 1-28, and are colour-coded green (1-7), peach (8-14), blue (15-21), pink (22-28).
All guests attend all 4 courses and all 4 houses (the image shows all guests 1-28 in each of the courses and in each of the houses). They do this in groups of 7 (of which there are 16, all unique).
No one attends...
(a) the same house more than once, nor
(b) the same course more than once.
Everyone...
(a) fails to meet many of the other guests, and
(b) meets several guests more than once (the colour-coding helps identify that).
...at least 8 in some venues is needed.
So far I haven't come up with a plan using 8 people at each venue.
Same here... ![]()
#16 Re: Help Me ! » Is velocity ever a scalar quantity? » 2025-02-24 02:10:57
Any ideas on the dinner party post?
Sorry Bob, but I've got no real clues on how to go about solving that one.
I don't know how to solve progressive dinners with formulas (bobbym had some success, with Mathematica).
And so I tried with Excel (like I've done successfully with a couple in the past), but no such luck this time.
#17 Re: Help Me ! » Is velocity ever a scalar quantity? » 2025-02-19 10:25:42
Echo_23's last post (#13) appends a paragraph that doesn't appear in paulb203's post #1...
#18 Re: Help Me ! » How many integers between 1 and 999 have 3 divisors? » 2025-01-21 08:18:34
Do you study about computer science?
No, not at all.
I just love doing number puzzles, with or without computer aided software.
For me, tackling a challenging number puzzle is simply a nice way to relax. ![]()
#19 Re: Help Me ! » How many integers between 1 and 999 have 3 divisors? » 2025-01-21 01:21:37
Hi ktesla39;
I revised my code to be much more Mathematica-like:
Code:
Length[Cases[Table[Divisors[i++],{i,999}],{_,_,_}]]
Output:
11
#20 Re: Help Me ! » How many integers between 1 and 999 have 3 divisors? » 2025-01-21 00:34:36
Hi ktesla39;
By the way, which language did you use in that program? It looks like python, is it?
No, it's not Python.
Mathematica has its own [proprietary] language, and you need to have the program (not free) to run the code.
I only have a basic knowledge of programming in it, as any Mathematica coder would quickly see if they saw my code.
I'm more familiar with BASIC, and was able to use some of that knowledge in Mathematica, which can run adjusted BASIC-like code, but with reduced efficiency compared to its own language.
#21 Re: Help Me ! » How many integers between 1 and 999 have 3 divisors? » 2025-01-20 17:08:44
Hi ktesla39,
I'll try python or JS automation to solve the question by dividing all integers from 1-999.
Good idea...I tried it with Mathematica, and here's my code and solution:
It tested all integers in that range, and for each integer that had only 3 divisors it printed the solution number, the integer number, and the divisors. When done, it gave the total number of solutions.
![]()
Edit:
#22 Re: Exercises » Exercise » 2025-01-14 02:07:32
Hi Bob;
Thanks for your method...I'll have to look at it tomorrow (bed now).
But before I go, here's my method:
![]()
#23 Re: Exercises » Exercise » 2025-01-13 08:55:10
Hi Bob;
Yes, I got that answer too...with a 27-character Mathematica formula using Sum & Mod that also runs in WolframAlpha.
#24 Re: Maths Is Fun - Suggestions and Comments » Avatar » 2024-12-15 23:17:53
Hi;
Whether I'm logged in or out, I get this message: "You do not have permission to access this page."
#25 Re: Help Me ! » Calculate the area of a triangle » 2024-12-14 14:05:30
Hi Kerim;
...there are more than one value for the triangle area that satisfies the given condition.
Reading the question on the OP, one has the impression that there is just one.
Yes, I have the same impression.
That's why I wrote these:
Post #2 - "or maybe there's some info missing"
Post #4 - "the OP's problem doesn't say anything about the sought area size"
Post #7 - "I would've thought that, ideally, there'd only be one location for the smallest AE+BG, and that we'd only need to report the area of CEG at that location.
So maybe the OP's wording in post #1 is missing some information we need?"
The only satisfactory goal (for when AE+BG is smallest) has to be to find either:
(a) the largest CEG area; or
(b) the smallest CEG area.
The number of different CEG areas in between (a) & (b) is infinite.
I'm opting for (b), as (a) is too easy. But maybe it's supposed to be an easy puzzle?! ![]()
Unfortunately, the OP hasn't returned to the thread to clarify...