Posts by mikau

mikau · Dark Discussions at Cafe Infinity

one of my scholarship search websites asks you to provide an answer to this question as part of your profile information. But its such a great question, I thought its worth posting elsewhere!

Here are several ways in which i would move mount Fuji:

-first try diplomacy

-find out what mountains eat and leave a trail of those in the desired direction

-move everything that isn't Mount Fuji in the opposite direction

-find another mountain and swap their names

-cut and paste

-cite is as illegally parked and have it towed (or just install a parking meter beside it)

-use a shovel

How would YOU move mount Fuji?

mikau · This is Cool

here we go, a quick modification to the playGame function:

public static int playGame()
{
  // simulates a game, returns the number of rolls

  int location=0;
  int diceRolls=0;
  boolean gameover=false;
  int roll=0;

  while (!gameover)
  {

      roll=diceRoll();
      diceRolls++;

      if (roll + location <= 100)
      {
		  location+=roll;
      	  location=additionalJumps(location); // jump forward if necessary


      	  if (location == 100)
      	  gameover=true;
       }

   }

   return diceRolls;

}

result of 10 million games:

Finished! average number of rolls: 39.2347894
Press any key to continue . . .

Looks like 39 rolls was correct after all!

mikau · This is Cool

good point.. but is that an official rule?

well if you consider that it takes approximately 36 moves to cross the board, according to my program, and it should take on average, 6 more rolls to land exactly on the finish line, that comes out to be 42. A hasty and imperfect analysis but the 42 answer would make sense.

I'll modify my program tomorrow to prevent it from going beyond 100.

mikau · This is Cool

39.59? Are you sure?

I wrote a simple simulation, and ran it twice, playing 1 million games each time. The average was about 35.8 with the 4th significant digit varying. Then I ran it twice, playing ten million games each time, and it also produced 35.8 with a varying 4th digit. The consistency seems pretty convincing..

Anyway, here is my program for anyone who is curious. The real meat of the program is the first two functions. Its written in Java, and pretty easy to read.

public class ChutesAndLadders
{
   // a program to simulate chutes and ladders games
   // and measure the average number of rolls to win

public static int playGame()
{
  // simulates a game, returns the number of rolls

  int location=0;
  int diceRolls=0;
  boolean gameover=false;


  while (!gameover)
  {

      location+=diceRoll();
      diceRolls++;
      location=additionalJumps(location); // jump forward if necessary


      if (location >= 100)
      gameover=true;

   }

   return diceRolls;

}

public static void main(String[] args)
{

	// play this many games
	int numGames=10000000; // ten million

	long totalRolls=0;

	for (int i = 0; i < numGames; i++)
	{
		totalRolls+=playGame();
	}

	double average=totalRolls/(double)(numGames);
	System.out.println("Finished! average number of rolls: " + average);
}

public static int diceRoll()
{
	// simulates a dice roll
	return 1 + (int)(6*Math.random());
}

public static int additionalJumps(int location)
{
	/* returns the location of the other end of a slide or ladder
	// if 'location' falls on one,
	// Returns the original location otherwise*/

	switch(location)
	{

	case 1: location=38; break;
	case 4: location= 14; break;
	case 9: location= 31; break;
	case 16: location= 6; break;
	case 21: location= 42; break;
	case 28: location= 84; break;
	case 36: location= 44; break;
	case 47: location=26; break;
	case 49: location= 11; break;
	case 51: location= 67; break;
	case 56: location= 53; break;
	case 62: location= 19; break;
	case 64: location= 60; break;
	case 71: location=91; break;
	case 80: location= 100; break;
	case 87: location= 24; break;
	case 93: location= 73; break;
	case 95: location= 75; break;
	case 98: location= 78; break;


	}


	return location;
}



}

output:

Finished! average number of rolls: 35.8300908
Press any key to continue . . .

mikau · This is Cool

we just need to write a truly random number generator first! ;]

that sounds like fun though, i think i'm going to do it! thanks for the suggestion, i'll post my results later.

mikau · This is Cool

An interesting problem that occured to me..

In the classic game of chutes and ladders, what is the average number of dice rolls to win?

mikau · Dark Discussions at Cafe Infinity

You seem to be under the impression that a calculator understands which decimals are correct and which are not.

I am under the impression that there are methods to determine how accurate an approximation (such as a taylor series) is, and how many terms are needed fora given error bound. So if we have a calculator with n digits, take the error bound to be 10^(-n) and add as many as necessary. Do calculators seriously not do this? If not, that's depressing!

In any case, i'd say there's a fundamental difference in the situations here:

in your case, i believe there are 6 operations (square root, multiplication, addition, square root, division) and thus an accumulation of errors.

what I was saying (although i didn't make it precise enough) is if f(x) is a function on the calculator, and you take f(a), (with 'a' a decimal number with n or less digits, n the number of digits on the display) then the result (on a good calculator) should be correct to the first n-1 digits.

I'm not saying that ln(sqrt(2)) is necessarily going to give good results on a 6 digit calculator, but it should give the natural log of '1.41421' (which is not the same thing) correct to 5 decimal places.

In otherwords, I think the calculator accurately calculates f(x), given that x is a quantity that can be completely described with no more than n decimal places. Thus I'd say log(5.1^2) is accurate to at least n-1 decimal places, but log(sqrt(2)) may not be, because we end up taking the log of the approximation of root 2.

mikau · Dark Discussions at Cafe Infinity

but that maaay be a little harsh, Jane. This is the first time I've EVER caught this particular teacher making a mistake on a proof. He's usually extremely good, which is perhaps why he didn't think to recheck his argument when my calculator disagreed, he's almost always right.

like i said i can forgive him for an honest mistake, i'm just a bit perplexed by what little regard he has for the accuracy of a modern calculator...

(edit) and i don't know why but i'm just loving the font i used in that diagram.. talk about style!

mikau · Dark Discussions at Cafe Infinity

Sure! Here was his argument:

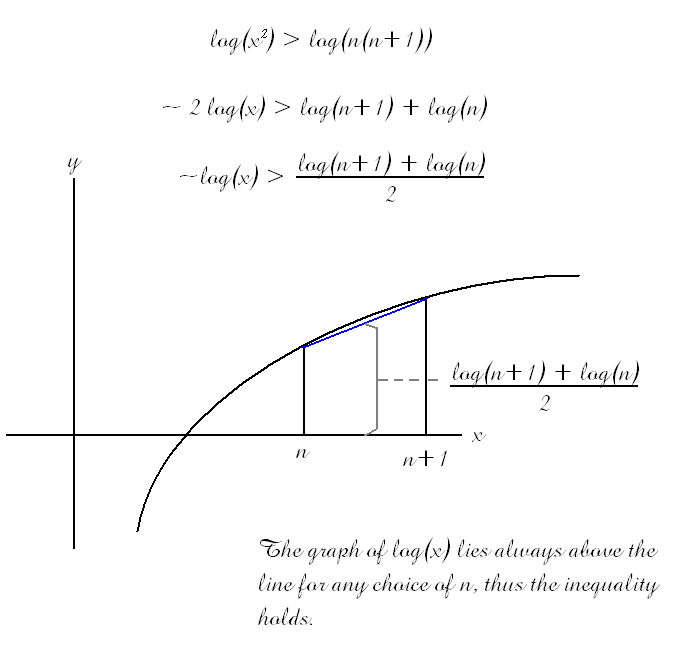
that last sentence is copied directly from his proof. Can you spot the error? Its kind of a fun problem, actually... one of my old calculus teachers used to give 'spot the error' problems, i tend to enjoy them.

mikau · Dark Discussions at Cafe Infinity

so on my last discrete math II class we were given the following question:

for all n ∈ N and x ∈ R, with n < x < n+1, prove that log(x^2) > log(n^2 + n)

I tackled the problem for 20 minutes without success, and then suddenly realized, it was definitely wrong. I grabbed my calculator and chose n = 5, and x = 5.1, and computed:

log(x^2) = log(5.1^2)=3.258...

log(n^2+n) = log(30) = 3.401...

i then wrote 'The claim is false' on the exam sheet, and gave the above calculations to support it, to receive credit for the problem.

After getting the exam back, my teacher laughed at me and said my 'disproof by calculator' was garbage, and reprimanded me for trusting the accuracy of its calculations. He then gave us his own 'proof' of the claim.

but I trusted my calculator more than that, however, i had to play by his rules. So this time i said:
4 < 6 < 9 ⇒ 2 < sqrt(6) < 3

so take n = 2 and x = sqrt(6)

and the claim:
log(x^2) > log(n^2 + n) ⇒ log(6) > log(6) which is obviously false, no calculators needed.

THIS the teacher couldn't ignore, although he was puzzled since he had his own proof of the claim. THEN I discovered and pointed out the error in his proof, which he acknowledged. He gave the whole class full credit for the problem (which was a big deal since not one person managed to do it, and many people did poorly on the test as it was) however he was still puzzled because he was sure this was true by another line of reasoning, and he was so distressed by it that he dismissed the class early.

I don't hold him in contempt for making this mistake, but i do find it surprising that he distrusted the accuracy of a calculator so much, that he didn't even bother to recheck the validity of his claim and instead assumed my calculator was inaccurate to as little as 2 decimal places. In fact, my calculator gives me 9 digits after the decimal place.. why would it bother to give me 9 if the first 2 were not reliable?

so after the test i argued that although calculators may use series approximations, we have methods by which we can determine the error bound, and i am certain our calculators use them to ensure it is accurate to as many digits as are given on the display. He, however, greatly doubted calculators were this sophisticated, and insisted they can never be trusted.

Now i understand that a calculator only gives an approximation, but I at least trust the first n-1 digits if n are given. Is this unreasonable? what do YOU think?

mikau · Help Me !

mikau · Help Me !

Set up the limits of integration for ∫ dV over R where R is the solid formed by the intersection of the parabolic cylinder: z=4-x[sup]2[/sup], the planes z=0, y = x, and y = 0.

Use the following orders of integration:

(1) dx dy dz
(2) dz dx dy

(1)
begining with z, z sweeps from 0 to 4

y then sweeps from 0 to the y height of the intersection of the cylinder z=4-x[sup]2[/sup] and the plane y=x, and so we have z=4-y[sup]2[/sup] so y = sqrt(4-z). So y sweeps from 0 to sqrt(4-z)

laslty, x (to my understanding) should sweep from the plane y=x, to the cylinder z=4-x[sup]2[/sup], and so x should sweep from y to sqrt(4-z)

my textbook gives x sweeping from 0 to 2.

(2)
starting with y, y sweeps from 0 to 2

x then sweeps from the plane y=x to 2, that is, from y to 2 (my textbook says from 0 to y)

lastly, z sweeps from 0 to the cylinder z=4-x[sup]2[/sup] so z sweeps from 0 to 4-x[sup]2[/sup]

again, disagreement with the textbook. What am I doing wrong?

mikau · Help Me !

The following is a homework assignment i need to turn in. I am allowed to seek help.

The prices of two articles, tax included are (a)$ and (b)$ respectively. Find the least and the largest number of units of each that can be bought with (c)$.

So in effect we must solve:
ax + by = c

in the actual problem the values are given but i'd rather solve it myself, moreover, I'd prefer hints, to a direct solution.

My biggest problem is I don't understand what is meant by the 'least' and 'largest' number of units of each.

I think i can solve it by considering that both x and y must be positive, and divisibility, but I believe we are supposed to use the Euclidean algorithm to solve this. But I thought that only finds one particular solution, with no special properties.

mikau · Help Me !

Incidentally, remember how i asked you what the difference between Vector and Multivariable Calculus was?? well, for some reason my school (attempts) to teach both in one course. So maybe the problems wouldn't be so different? I don't know.

Anyway, so from the above discussion, we have the derivative of T would be an (m*n)x(n) matrix, which i presume we could multiply by an nx1 vector (the point in question) to get an (m*n)x1 vector, which techinically represents an m x n matrix ( i guess?). And we could multiply this by an nx1 vector again to obtain a vector in R^m. Do these operations mean anything?

I ask because my book points out that we can right multiply D[sub]x0[/sub](T) = D[sup]2[/sup][sub]x0[/sub](f) first by x1 in R^n to obtain an element of L(R^n, R^m), and then right multiply again by x2 in R^n, to obtain an element in R^m, and thus construct a bilinear mapping B:

R[sup]n[/sup] x R[sup]n[/sup] -> L(R[sup]n[/sup], R[sup]m[/sup])
B: (x1, x2) -> D[sup]2[/sup][sub]x0[/sub](f)(x1,x2)

whats does this mapping represent? and um... shouldn't B go to R^m?

mikau · Help Me !

Thanks, Ricky. I didn't have time to look at this till just now. Trying to spend time actually understanding the underlying theory in this course has just been holding me back, as my teachers unpublished textbook is so riddled with error, I don't have time to clarify every detail and keep up with the pace of the course. It really makes me sad.. topics being presented for the first time really need to be straight in order to make sense. You can't learn this way...

i 'll have to buy a published textbook on vector calc and teach myself over the winter i guess. Seems to be the only proper way to learn anything these days..

But I will do my best to understand what you just explained, thank you for that.

mikau · Help Me !

as far as I can see, what you did was take a function:

f(x) = x^2,

took the derivative mapping:

f'(x) = [2x]

evaluated it at 2,

f'(2) = 4,

and constructed a new mapping from this:

g(x) = 4x

and took the derivative of this to get 4 again.
This seems, in no way, analogous to second, or even first derivative. I chose g(x), but you wrote f'(x) = 4x after saying f(x) = x^2, and that just makes me want to scream.

Furthermore, I'd have said the second derivative of f(x) = x^2 was 2, not 4.

"Remember that a linear map is just a special type of map, or rather, function. As such, it can be differentiated like any other function."
You see, the problem is i see T as a function that creates a linear map, not a linear map itself, and hence the notion of derivative escapes me. T, to my understanding, maps to a matrix, but to make a linear mapping (call it g), we need to grab the resulting matrix at a particular point, and say g(x) = Ax.

moreover, since the derivative of a linear map is just the linear map itself, it seems by this reasoning that the 2nd, 3rd, 4th, n'th derivative, with n > 1, is just A.

"A derivative is a matrix of partials, and if you plug in a point x_0, you get a matrix of real numbers. It is the real numbers which is an element of L(R^n, R^m). This is why the derivative T is a function from R^n to L(R^n, R^m)."

see, this is the part i don't get. I thought it said T was the function that produces an element of L(R^n, R^m). T maps x to D[sub]x[/sub](f), so we plug in a value of x, and we get a mapping in L(R^n, R^m). Makes sense, but i don't see why the derivative of T would be a function from R^n to L(R^n, R^m).

Goodness, I'm confounded..

mikau · Help Me !

Thanks for the response, Ricky. Its pretty late right now and i don't have the time or energy to read it now, but I'll check it tomorrow. Much appreciated!

mikau · Dark Discussions at Cafe Infinity

Is math a science? Isn't that entirely up to Zach?

mikau · Help Me !

my book lost me with this introduction of the second derivative:

to define an analogue for the second derivative, let us consider the following. Let

And there you lost me... I don't understand exactly how we are taking the derivative of a linear mapping, which to my understanding, is just a matrix thats a function of x[sub]0[/sub].

Particularly because of my following observation:
let f: R[sup]n[/sup] to R[sup]m[/sup].
Then the derivative of f is an m x n matrix such that when right multiplied by an element of the domain (an n x 1 vector) you obtain an element of the target set (an m x 1 vector).

Likewise, if T: R[sup]n[/sup] to M[sub] m x n[/sub] (meaning the space of mxn matrices, or equivalantly the space of linear maps from R[sup]n[/sup] to R[sup]m[/sup]), then the derivative of f should (by my understanding) be a matrix such that when right multiplied by an (n x 1) vector in the domain, gives you an m x n matrix. But obviously, right multiplication of any matrix by an n x 1 vector cannot produce an m x n matrix.

Hence, I lose grasp on the meaning of the derivative in this context. By my understanding, the derivative must produce a linear map from the departure space to the arrival space, but the linear map (appearantly) cannot be represented by a matrix, which simply can't be true!

Can someone clarify whats wrong with my reasoning here?

mikau · Euler Avenue

I find it interesting that so many of these challenges involve applying mathematics to biology. It would be cool if mathematicians could supply assistance to the important study of biology as much as possible, since I would assume most biologists are not advanced mathematicians, and that skill may be able to advance our understanding of the subject, or any subject, more than we realize.

mikau · Help Me !

I'm not sure but, but I think the integral can't be simplified much more unless you are given the velocity function (dx/dt).

mikau · Help Me !

let f(x,y,z) = x + y^2 -z^2

find the equation of the tangent plane to f at (1,2,3).

The book then proceeds to construct a plane in 3 variables by some logic that escapes me. I don't understand this geometrically. The graph of this is in 4 dimensions. How can a plane in 3 dimensional space, be tangent to a 4 dimensional graph.

Now, if we were to set: f(x,y,z) = K, now we've got a 3d surface that kinda makes sense to me. We then know that the gradient vector is perpendicular to this at the point (x,y,z), and we construct a tangent plane. However, if we're going to let f(x,y,z) = K, then we must let K = f(1,2,3) since we're assuming the graph passes though this point.

So is this problem really asking me to consider a 4 dimensional graph, or the graph of f(x,y,z) = f(1,2,3) ???

further, consider the next problem:
Find the direction of the greatest rate of increase of f(x,y,z) = xye^z at the point (2,1,2)

again, we seem to be considering a 3 dimensional surface, whereas the graph is, I think, in 4 dimensions. So whats going on? Am I not understanding, or is this being presented in a screwy manner?

mikau · Coder's Corner

At least as far as we know right now.

right now? so you mean, we don't know for sure that such an algorithm can't exist?

mikau · Coder's Corner

Suppose we had a function firstDivisor(unsigned int n) that returns the smallest divisor of n. Observe this number is always prime, and when n is prime, the output is n itself.

Is it possible that such an algorithm could be O(log n)? I was wondering if I could construct one today, (hoping to move another algorithm from O(n^2) to O(n log n) )

but since the output of firstDivisor is n when n is prime, we can create a primality test by the expression:
(n == firstDivisor(n));

and thus have a primality test thats O(log n). Is such an algorithm possible?

mikau · Help Me !

So yes, that step is valid, though written rather oddly.

how would you write it? (a non odd fashion)

Math Is Fun Forum

#26 Dark Discussions at Cafe Infinity » How would you move Mnt. Fuji? » 2009-06-27 18:19:46

#27 Re: This is Cool » Chutes and Ladders » 2009-05-19 08:05:35

#28 Re: This is Cool » Chutes and Ladders » 2009-05-18 19:57:19

#29 Re: This is Cool » Chutes and Ladders » 2009-05-18 18:52:58

#30 Re: This is Cool » Chutes and Ladders » 2009-05-18 17:05:00

#31 This is Cool » Chutes and Ladders » 2009-05-18 14:40:05

#32 Re: Dark Discussions at Cafe Infinity » using calculators as proof » 2009-04-17 17:12:09

#33 Re: Dark Discussions at Cafe Infinity » using calculators as proof » 2009-04-16 19:35:57

#34 Re: Dark Discussions at Cafe Infinity » using calculators as proof » 2009-04-16 15:34:48

#35 Dark Discussions at Cafe Infinity » using calculators as proof » 2009-04-16 13:41:43

#36 Re: Help Me ! » LaTeX - A Crash Course » 2009-02-14 09:53:41

#37 Help Me ! » limits of integration for Triple Integral » 2008-11-28 08:36:06

#38 Help Me ! » Diaphantine equations » 2008-11-03 00:47:43

#39 Re: Help Me ! » second derivative in multivariable functions » 2008-10-27 08:22:38

#40 Re: Help Me ! » second derivative in multivariable functions » 2008-10-27 07:33:51

#41 Re: Help Me ! » second derivative in multivariable functions » 2008-10-18 06:08:02

#42 Re: Help Me ! » second derivative in multivariable functions » 2008-10-16 17:38:08

#43 Re: Dark Discussions at Cafe Infinity » Debate #001: Is math a science? » 2008-10-16 13:23:07

#44 Help Me ! » second derivative in multivariable functions » 2008-10-16 09:25:23

#45 Re: Euler Avenue » DARPA Mathematical Challenges » 2008-09-30 03:18:51

#46 Re: Help Me ! » Integration Help » 2008-09-28 23:48:46

#47 Help Me ! » tangent plane to a curve » 2008-09-28 14:34:58

#48 Re: Coder's Corner » time complexity of divisibilty/primality » 2008-09-27 17:26:06

#49 Coder's Corner » time complexity of divisibilty/primality » 2008-09-27 11:31:51

#50 Re: Help Me ! » derivatives in multiple variables » 2008-09-26 17:49:27

Board footer