Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#1 2016-02-13 20:46:33
- BernardBeduya
- Guest
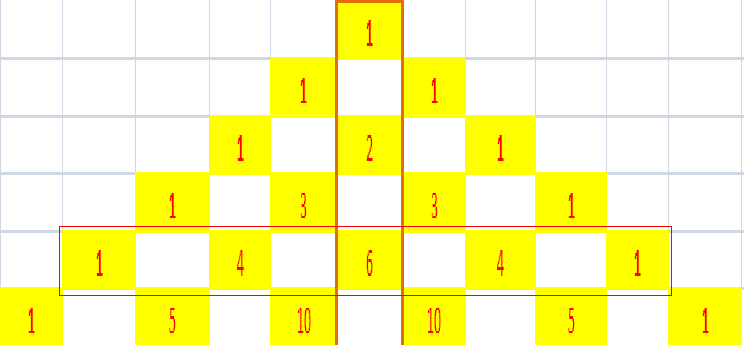
A Pascal's Triangle Hidden Inside the Pascal's Triangle
Hi! I was referred by Rod to this forum.
May I invite you to click the link below to my wordpress blog with the title `A Hiddren Pascal`s Triangle Hidden Inside the Pascal`s Triangle`.
https://bernardbeduya.wordpress.com/2016/02/06/a-pascals-triangle-hidden-inside-the-pascals-triangle/
Please help me make sense of my discovery because I`m not an expert mathematician as you. Thank you and warm regards.
#2 2016-02-13 22:41:58
- Nehushtan
- Member

- Registered: 2013-03-09
- Posts: 957
Re: A Pascal's Triangle Hidden Inside the Pascal's Triangle
I disagree with this statement from the website:
The same phenomenon appears where the row that bears the numbers 1-4-6-4-1 is the last palindromic sequence.
No, it is not! It is only the last because we are using base 10. If we use higher bases, the palindromic sequence will continue; e.g. in hexadecimal base, the next line would be 1-5-A-A-5-1; and in a still higher base (> 20) the next line would be 1-6-F-K-F-6-1. As you can see, any line in Pascal's triangle can be palindromic, if you choose a high-enough base.
As for the number 1001, it is of the form n³+1 = (n+1)(n²−n+1), where n is the base; hence it is composite regardless of the base chosen. If a number is composite, I'd say it has a good chance of appearing in Pascal's triangle.
Please help me make sense of my discovery because I`m not an expert mathematician as you. Thank you and warm regards.
All you need to know is that mathematics is always a very curious and interesting subject.
240 books currently added on Goodreads
Offline
#3 2016-02-13 23:11:50
- Nehushtan
- Member

- Registered: 2013-03-09
- Posts: 957
Re: A Pascal's Triangle Hidden Inside the Pascal's Triangle
On the subject of palindromic numbers, note the following:
[list=*]
[*]
[/list]
These are successive powers of n+1, where n is our base; they're palindromic up to some point depending on n. For base 10 (n=10) the palindromicity breaks down at the fifth power, when carrying-over starts to take over:
[list=*]
[*]
[/list]
To continue the palindromic sequence, all you need to do is choose a higher base (n>10). For example, consider the powers of 17 in hexadecimal:
[list=*]
[*]
[/list]
Ta da! Whereas (10+1)⁵ fails to be palindromic in base 10, (16+1)⁵ is palindromic in base 16. Choose n > 20 and (n+1)⁶ will be palindromic in base n too.
Last edited by Nehushtan (2016-02-13 23:18:31)
240 books currently added on Goodreads
Offline
#4 2016-02-14 07:27:52
- anonimnystefy
- Real Member

- From: Harlan's World
- Registered: 2011-05-23
- Posts: 16,049
Re: A Pascal's Triangle Hidden Inside the Pascal's Triangle
Hej, Bernard!
I am failing to see how the "hidden" triangle is different from just the Pascal's triangle multiplied by 1001 and inserted somewhere in-between the numbers of a regular Pascal triangle?
Here lies the reader who will never open this book. He is forever dead.
Taking a new step, uttering a new word, is what people fear most. ― Fyodor Dostoyevsky, Crime and Punishment
The knowledge of some things as a function of age is a delta function.
Offline
#5 2016-06-22 21:45:15
- beduya22
- Member
- Registered: 2016-06-22
- Posts: 2
Re: A Pascal's Triangle Hidden Inside the Pascal's Triangle
Thank you Nehushtan and anonimnystefy for helping me. Sorry I wasn't able to return to this forum soon because I was busy with work. I'm trying to edit my wordpress blog now. I really couldn't have realized that it was wrong for me to think of decimal digits only without your help. With regards to anonimnystefy's message, it's really no different from just a Pascal's triangle multiplied by 1001 but my goal in inserting this starting at the 13th row of the original Pascal's triangle was because I noticed that there are 4-digit palindromic numbers 1001, 2002 and 3003 in the 14th row, and 3003 and 5005 in the 15th and then 8008 in the 16th row, forming a shape of an inverted triangle. I then wondered why 4004, 6006, 7007 and 9009 are missing in this region of the original Pascal's triangle. That's why I conjectured that if I placed the 1st palindromic number 1001 on top of 2002 in the original Pascal's triangle and use that 1001 as the border numbers of my inserted Pascal's triangle, I might be able to locate those missing 4-digit palindromic numbers that I mentioned. So, when I did see the completed 4-digit palindromic numbers in my inserted Pascal's triangle, I just wondered why this is so. Anyways, thanks for all your help guys.
Offline