Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2016-10-13 05:45:39
- sisyphus
- Member
- Registered: 2016-05-15
- Posts: 26
Orders of Growth
I'm reading the "structure and interpretation of computer programs" book (that i probably should not touch) and i'm trying to understand an explanation for an exercise.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Provided we have n types of coins 1, 5,10 ,25 ,50 (so if n = 3, then the type-of-coin(n) = 10), how many ways can we make change of m dollars (in cents)?
for f(m, n):
if m = 0 -> 1
if m < 0 or n = 0 -> 0
else -> f( m, (n - 1) ) + f( (m - type-of-coin(n)), n)
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
So the problem is "What are the orders of growth of the space and number of steps used by f(m, n) as m increases? ". The answer in http://wiki.drewhess.com/wiki/SICP_exercise_1.14 says that "It's then straightforward to show that the number of steps required to evaluate f(m 5) is θ(m^5). "
I don't understand what θ(m^5) means here, because if i take 11 cents and put it into the function above, i get f(11, 5) = 4 in 55 steps. Now if i take 12 cents, i get that f(12, 5) = 4 in 63 steps. So how should i interpret θ(m^5) here, 11^5 is 161051, not 55?
http://wiki.drewhess.com/wiki/SICP_exercise_1.14
https://tobilehman.com/images/blogimg/cc_11_5.png
https://mitpress.mit.edu/sicp/full-text/sicp/book/node17.html
Last edited by sisyphus (2016-10-13 05:59:25)
Offline
#2 2016-10-13 06:22:41
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Orders of Growth
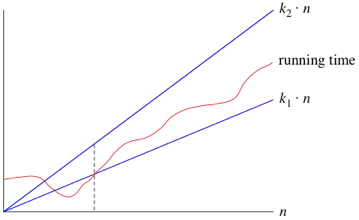
Supposedly that notation means that the process is bounded both above and below by m^5 but remember this is an asymptotic concept. This really only applies when n is very large.
The big Theta notation is less common than Big O. Rarely do we need the lower bound.
See if you can get a bit of help out of this:
https://www.khanacademy.org/computing/c … a-notation
Also, remember there are two constant multiples of m^5 that are left out.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#3 2016-10-13 07:01:30
- sisyphus
- Member
- Registered: 2016-05-15
- Posts: 26
Re: Orders of Growth
Ah, thanks for the link. I've tried bigger numbers for the function in my example and it seems to be slowly approaching m^5, although of course i could only try out numbers up to 700~, after that my cpu is done for. A supercomputer would be handy right now ![]() .
.
Offline
#4 2016-10-13 07:02:23
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Orders of Growth
Do not forget the constants, the graph shows that for low values f(n) can fall out of the bounds.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
Pages: 1