Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2022-05-06 15:03:48
- mathdrop
- Member
- Registered: 2022-03-07
- Posts: 75
Circle on hyperbola
This is about putting a circle on top of a hyperbola
(a*sqrt(b^2+x^2))/b, where a = semi major axis and b = semi minor axis,
so that they have one point in common,
while the center of the circle matches, or is close to, a given x.
How to do it ?
Offline
#2 2022-09-18 14:38:58
- mathdrop
- Member
- Registered: 2022-03-07
- Posts: 75
Re: Circle on hyperbola
It is that my PC was a little sketchy, using my approach,
But since there were no other suggestions,
I guess I will go down that route.
So, Imagine the friendly circle sitting peacefully on the arm of the hyperbola.
Now, let's see if it would help, if we draw a triangle into it.
It's hypotenuse goes from the center of the circle A
to the intersection with the hyperbola B.
Moving horizontally over B gives us C.
The hypotenuse is always perpendicular
to the slope of the hyperbola in point B
and the angle on A is just angle=atan(slope in B).
The above enables us to put an approximate procedure.
For getting the first test value,
I use the angle of the hyperbolas asymptotes (e.g. at 45°).
I use trigonometry to get the x value.
Then I check what slope the hyperbola at that x-value has
and convert it to an angle. It will be flatter.
Than I again use trigonometry to get the x value. And so forth.
This should converge to the desired x value
in ever smaller steps.
If the (angle)change falls under a certain threshold,
I stop it and take the value.
So much for now. Maybe later some more details and stuff.
Edit: I called a point wrong; "under A" => "over B" (complementary angle meant before)
Last edited by mathdrop (2022-11-20 17:28:36)
Offline
#3 2022-09-18 20:28:56
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: Circle on hyperbola
hi mathdrop,
I seem to have missed this thread; sorry ![]()
To make a graph, initially, I chose a=6 and b=4. That meant the circle would have to be under the hyperbola so I tried again with b = -4 and got this:

Is that the sort of thing you want?
Has both axes as lines of symmetry.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#4 2022-10-18 07:30:04
- mathdrop
- Member
- Registered: 2022-03-07
- Posts: 75
Re: Circle on hyperbola
Thank you, Bob :-)
We take your initial choice
and flip the circle to the inside of the hyperbola,
so it resembles a ball in a ditch.
Now we push it a little uphill and freeze.
What is it's Y-Value ?
Edit: Being more specific.
Last edited by mathdrop (2022-10-18 09:20:41)
Offline
#5 2022-10-18 22:48:46
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: Circle on hyperbola
Diagram 2:

Is this more like it?
You'd have to know the a and b values and the radius of the circle. AB is at right angles to the common tangent. That should help.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#6 2022-10-27 00:40:44
- mathdrop
- Member
- Registered: 2022-03-07
- Posts: 75
Re: Circle on hyperbola
You nailed the graph :-)
(One could consider, if one wants the radius of the circle
to be the same as in the apex of the hyperbola (called vertex),
but this is not fix and thus not required.
However, a bigger circle is limiting the range of the x-shifting.)
As you can see, I'm still trying
to improve making me understood ;-)
But it might be worth while, so of it is bearable,
I would probably go on with that for a while.
Nice Drawings, by the way.
Which Software do you use ?
Is there something comparable in Linux ?
I do not have B and just the x-value of A.
I however have the radius an thus
the distance between A and B.
I also have the hyperbola.
The y-value of A should be wherever he circle
has one single point in common with the hyperbola,
on which it also shares the same slope with the hyperbola.
For r_circle<=r_vertex:
If one would roll the ball trough the ditch,
its center would draw another hyperbola, right ?
Offline
#7 2022-10-27 21:14:23
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: Circle on hyperbola
I use Geometers Sketchpad. Other members prefer Geogebra which is free. It has some features that Sketchpad lacks, but I like the clear appearance of the diagrams I can produce.
Using A (p,q) and B (s,t) and radius r, I've had a 'play' with this. The equations get really horrible. It would be a lot easier if I could use numbers rather than letters.
My method:
Form an equation for the gradient of AB in terms of p,q,s,t.
Differentiate the hyperbola to get the gradient at B.
These two are perpendicular so product of gradients = -1.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#8 2022-10-27 21:17:21
- John John
- Member
- From: Umuahia, Abia state, Nigeria
- Registered: 2022-10-25
- Posts: 24
Re: Circle on hyperbola
Hello guys can i get some permutation questions
The golden rule in maths don't find x if you don't know where y is-jjc
Offline
#9 2022-10-27 21:26:16
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: Circle on hyperbola
hi John John
Yes but please be more specific. The MIF teaching pages has this:
https://www.mathsisfun.com/combinatoric … tions.html
At the bottom of the page you will find some test yourself questions.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#10 2022-10-27 21:55:05
- John John
- Member
- From: Umuahia, Abia state, Nigeria
- Registered: 2022-10-25
- Posts: 24
Re: Circle on hyperbola
Ok
The golden rule in maths don't find x if you don't know where y is-jjc
Offline
#11 2022-10-30 02:13:23
- mathdrop
- Member
- Registered: 2022-03-07
- Posts: 75
Re: Circle on hyperbola
It would be nice, if you could try to show me
the right y for a given x (q and p in your example),
with specific number pickings.
As a test, I would also run your numbers
through the approximate procedure,
which I outlined in my second post in this thread.
So, let's go ;-)
Offline
#12 2022-10-31 02:42:02
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: Circle on hyperbola
Took a while to find 'nice' numbers. I have
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#13 2022-11-02 09:28:13
- mathdrop
- Member
- Registered: 2022-03-07
- Posts: 75
Re: Circle on hyperbola
What does A and B mean in your last post ?
I would need an x-value for the center of the circle.
Offline
#14 2022-11-02 21:11:56
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: Circle on hyperbola
see post #5
B
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#15 2022-11-03 07:43:58
- mathdrop
- Member
- Registered: 2022-03-07
- Posts: 75
Re: Circle on hyperbola
At this point I have been looking for values to start out with.
It could probably help if you would denote your pickings and solutions, here.
Your x-value for the center of the circle is 0. What if it weren't 0 ?
In (a*sqrt(b^2+x^2))/b you have taken a=6 (also y-intercept) and b=3 (sqrt(9)).
Why have you picked such an uneven radius or is it part of a solution ?
According to your description,
there is no radius length in your equations.
Since the radius is constant, this could be a problem.
Following your approach a few steps:
A=(x1,y1); B(x2,y2)
m=((x2-x1)/(y2-y1))
A=(p,q); B(s,t)
m=((s-p)/(t-q))
g(x)=m*x+b
g(x):=((s-p)/(t-q))*x+b
g'(x):=(s-p)/(t-q)=d/dx(g(x)) // 1st derivative
f(x):=2*sqrt(9+x²)
f'(x):=2*x/sqrt(9+x²)=d/dx(f(x)) // 1st derivative
g'(x)*f'(x)=-1 // perpedicularity
(((s-p)/(t-q))*x+b)*(2*x*sqrt(9+x²))=-1
What have you done from there ?
I'm going to outline my approach in a separate posting.
Edit: Correcting mistake in f'(x)
Last edited by mathdrop (2022-11-06 14:47:28)
Offline
#16 2022-11-03 10:22:09
- mathdrop
- Member
- Registered: 2022-03-07
- Posts: 75
Re: Circle on hyperbola
It seems, that I just can not let go of your procedure yet.
How have you found what you call nice numbers ?
Another approach for what you gave me:
Where the distance between (a,b) and (c,d)
is the shortest, there is your circle.
Matching your second plot, it must be (6*sqrt(4²+x²))/4 <=> 3/2*sqrt(16+x²),
so a=6 and b=4, there. The x-value of the circles center is 4.
It's radius also is not a whole number. One could round it down to 2,
so I would pick 2. Such is what I thought about.
Can you give a solution to this, too ?
=> I'm not sure if it even is mathematically possible,
to answer such a question without an approximate procedure. <=
Or can you teach me otherwise ?
Altering the radius is the answer to another question,
but can your procedure find point B of your second plot,
if you alter the radius again (as drawn in the plot) ?
Edit: Remarking peak-value-approach for what you gave me.
Last edited by mathdrop (2022-11-03 11:02:01)
Offline
#17 2022-11-04 22:27:20
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: Circle on hyperbola
I started with
To keep the numbers small and whole (if possible) I chose b = 3 and the x coodinate of B as 4.
That gave y = 5a/3, so I further chose a = 6, giving y = 10.
Differentiating to get dy/dx at B gives a gradient at B of 8/5 and so AB has a gradient of -5/8.
So if A is on the y axis it has coordinates (0, 12.5)
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#18 2022-11-06 15:41:18
- mathdrop
- Member
- Registered: 2022-03-07
- Posts: 75
Re: Circle on hyperbola
(a*sqrt(b^2+x^2))/b = a/b*sqrt(b^2+x^2) // haven't initially seen this
Graphing your pickings (and my model of thinking) with GeoGebra: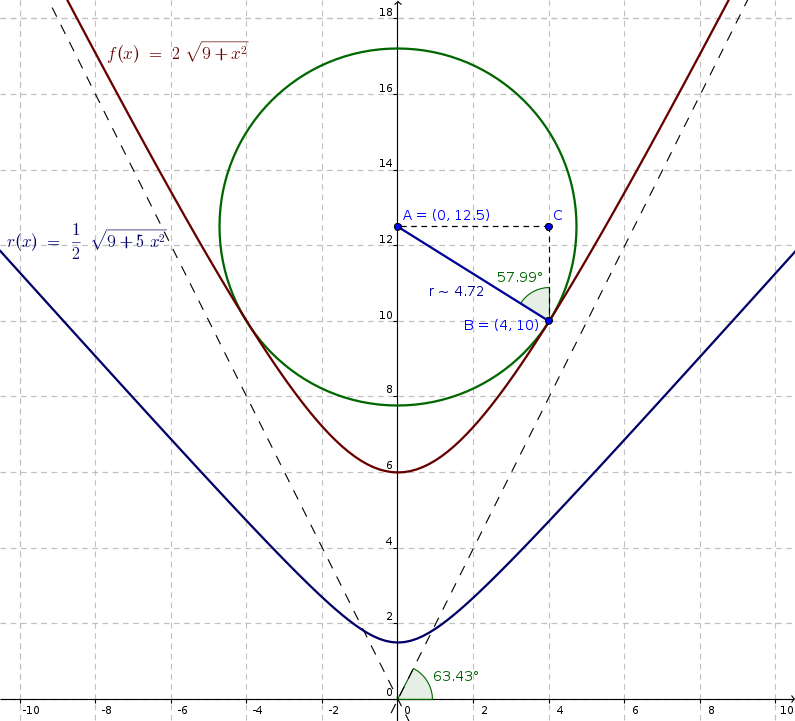
Old graph, which Bob referred to
Following your proceeding:
f'(x)=2*x/sqrt(9+x²)
f'(4)=2*4/sqrt(9+4²)=8/sqrt(9+16)=8/sqrt(25)=8/5
y=m*x+b <=> y-m*x=b | m=(8/5)^(-1)=-5/8, x=4, y=10
b=10-(-5/8*4)=10-(-20/8)=10-(-2.5)=10+2.5=12.5 // y-intercept
This ignores "while the center of the circle matches, or is close to, a given x"
in my questioning. And the radius is constant, as I mentioned later.
Edit: your radius. vector: r=(0-4,12.5-10)=(-4|2.5) |r|=sqrt((-4)²+2.5²)=sqrt(16+6.25)=sqrt(22.25)=sqrt(89)/2~4.716991, new graph
Last edited by mathdrop (2022-11-21 18:13:14)
Offline
#19 2022-11-06 19:26:02
- mathdrop
- Member
- Registered: 2022-03-07
- Posts: 75
Re: Circle on hyperbola
Thank you for the example with the nice numbers and the hint regarding GeoGebra.
Once, I looked at it shortly, but haven't thought it is that powerful.
Why are you almost the only one who is answering me ?
For my approach I would start out with the angle of the hyperbolas asymptotes alpha.
In English, you probably have a special word for them. Which is it again ?
Applying my approach:
alpha=atan(slope)
alpha=atan(+/- a/b)
alpha=atan(6/3)=atan(2)~63.4
sin(a)=opposite/hypotenuse
sin(a)*hypotenuse=opposite
sin(a)*r=x_offset
sin(atan(2))*sqrt(22.25)=~4.22
x_circle:=0
x_circle+x_offset=x_test_1
I'm going to continue here later.
Edit: alpha in degrees instead of radians, sine instead of cosine
Last edited by mathdrop (2022-11-21 12:21:51)
Offline
#20 2022-11-06 23:06:59
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: Circle on hyperbola
hi mathdrop
Great diagram!
I call them asymptotes too. I've looked around the internet and that looks like the correct term.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#21 2022-11-20 16:55:10
- mathdrop
- Member
- Registered: 2022-03-07
- Posts: 75
Re: Circle on hyperbola
f(x)=2*sqrt(9+x²)
f'(x)=2*x/sqrt(9+x²)
x_test_1 ~ sin(63.4)*4.72 = sin(atan(2))*sqrt(22.25) ~ 4.22
(sin(atan(2))*sqrt(22.25))² = 17.8
9+17.8 = 26.8
f'(~4.22) = 2*sin(atan(2))*sqrt(22.25)/sqrt(9+(sin(atan(2))*sqrt(22.25))²)
= 2*sin(atan(2))*sqrt(22.25)/sqrt(26.8)
~ 1.62
atan(~1.62)=atan(2*sin(atan(2))*sqrt(22.25)/sqrt(26.8))~58.5
x_test_2 ~ sin(58.5)*4.72 = sin(atan(2*sin(atan(2))*sqrt(22.25)/sqrt(26.8)))*sqrt(22.25)~4.02
(sin(atan(2*sin(atan(2))*sqrt(22.25)/sqrt(26.8)))*sqrt(22.25))² = 16 + 81/490
9 + 16 + 81/490 = 25 + 81/490
f'(~4.02) = 2*sin(atan(2*sin(atan(2))*sqrt(22.25)/sqrt(26.8)))*sqrt(22.25)/sqrt(9+(sin(atan(2*sin(atan(2))*sqrt(22.25)/sqrt(26.8)))*sqrt(22.25))²)
= 2*sin(atan(2*sin(atan(2))*sqrt(22.25)/sqrt(26.8)))*sqrt(22.25)/sqrt(25+81/490)
~ 1.60
atan(~1.60)=atan(2*sin(atan(2*sin(atan(2))*sqrt(22.25)/sqrt(26.8)))*sqrt(22.25)/sqrt(25+81/490))~58.0
x_test_3 ~ sin(58.0)*4.72 = sin(atan(2*sin(atan(2*sin(atan(2))*sqrt(22.25)/sqrt(26.8)))*sqrt(22.25)/sqrt(25+81/490)))*sqrt(22.25)~4.00
I don't mean to brag, but you see how fast it converges ? ;-)
With 3 significant digits it rounds to your exact number solution after only 3 iterations.
And it is applicable to another range of problems,
where exact numbers are perhaps not possible
(but very close ones probably are).
Do you follow my approach ?
The computer gives me wrong values, if I automate it completely.
Then I thought I could ask if I'm doing it right, but obviously it works on paper.
Regarding the word I heath some especially for hyperbolas.
I can put it if I come across it again.
Edit: saving in between
Last edited by mathdrop (2022-11-20 17:53:32)
Offline
#22 2022-11-21 10:44:18
- mathdrop
- Member
- Registered: 2022-03-07
- Posts: 75
Re: Circle on hyperbola
I'm trying to do the peakvalue-approach with your example here:
Tangent line: y=m*x+b
Normal line with m=-1/m <= m of tangent line
f(x)=2*sqrt(9+x²)
f'(x)=2*x/sqrt(9+x²)
n(x)=-1/f'(t)*(x-t)+f(t) // general normal line equation
n(x,t)=-1/(2*t/sqrt(9+t²))*(x-t)+2*sqrt(9+t²)
=2*sqrt(t^2+9)-(sqrt(t^2+9)*(x-t))/(2*t)
=(5*sqrt(t^2+9))/2 - (sqrt(t^2+9)*x)/(2*t)
=+/- (sqrt(t^2+9)*(5*t-x))/(2*t)
n(x,t):=(sqrt(t^2+9)*(5*t-x))/(2*t)
n(0,t)=(5/2)*sqrt(t^2+9)
n(t,t)=2*sqrt(t^2+9)=f(t)
t²+(n(0,t)-n(t,t))² = r² // pythagoras
r(t)=sqrt(t²+(n(0,t)-n(t,t))²)
r(t)=sqrt(t²+((5/2)*sqrt(t^2+9)-2*sqrt(t^2+9))²)=1/2*sqrt(5*t^2+9)
<=>
t(r)=+/- sqrt(4*r^2-9)/sqrt(5)
r(t): r(4)=1/2*sqrt(5*4^2+9)=sqrt(89)/2=sqrt(22.25)~4.72 gives your radius, see ?
n(x,r)=sqrt(r^2+9)*(sqrt(5)-x/sqrt(4*r^2-9))
=sqrt(5)*sqrt(r^2 + 9)-(sqrt(r^2+9)*x)/sqrt(4*r^2-9)
n(0,r)=sqrt(5)*sqrt(r^2+9)
n(0,~4.72)=sqrt(5)*sqrt((sqrt(89)/2)^2+9)=12.5 your y-circlecenter, see ?
Bob, it seems, that you had the critical hint, this time. Thank you.
Regarding peekvalue, the minimal radius is the one
of a circle with the curvature of the hyperbola in x=0 (see graph).
Edit: saving in between
Last edited by mathdrop (2022-11-21 15:54:38)
Offline
#23 2022-11-21 14:09:39
- mathdrop
- Member
- Registered: 2022-03-07
- Posts: 75
Re: Circle on hyperbola
More general approach:
Tangent line: y=m*x+b
Normal line with m=-1/m <= m of tangent line
f(x):=a/b*sqrt(b^2+x^2)
f'(x):=a*x/(b*sqrt(b^2+x^2))
j=:x0
n(x)=-1/f'(t)*(x-t)+f(t) // general normal line equation
n(x,t)=-1/(a*t/(b*sqrt(b^2+t^2)))*(x-t)+a/b*sqrt(b^2+t^2)
= sqrt(b^2+t^2)*(a/b-(b*(x-t))/(a*t))
= (sqrt(b^2+t^2)*(a^2*t+b^2*(t-x)))/(a*b*t)
=-b*x*sqrt(b^2+t^2)/(a*t) + a*sqrt(b^2+t^2)/b + b*sqrt(b^2+t^2)/a
q=:A1 // q=0 => circlecenter on y-axis
t=:C1
n(0,t)=((a^2+b^2)*sqrt(b^2+t^2))/(a*b)
=(a*sqrt(b^2+t^2))/b+(b*sqrt(b^2+t^2))/a
n(t,t)=a/b*sqrt(b^2+t^2)=f(t)
t²+(n(0,t)-n(t,t))² = r² // pythagoras
<=>
r(t)=sqrt(t²+(n(0,t)-n(t,t))²)
r(t)=sqrt((b^4+a^2*t^2+b^2*t^2)/a^2)
=sqrt((b^4+(a^2+b^2)*t^2)/a^2) // a,b,r real and positive
t(r)=+/- sqrt(-b^4+a^2*r^2)/sqrt(a^2+b^2)
=+/- sqrt((a^2*r^2-b^4)/(a^2+b^2)) // a,b,r real
r(0)=r(t), a=6, b=3, t=4 gives sqrt(89)/2~4,72
n(x,r)=sqrt((a^2*(b^2+r^2))/(a^2+b^2))*((b*(sqrt((a^2*r^2-b^4)/(a^2+b^2))-x))/(a*sqrt((a^2*r^2-b^4)/(a^2+b^2)))+a/b)
n(0,~4.72), a=6,b=3 = n(x,r), a=6, b=3, x=0, r=sqrt(89)/2 = 12.5
Still more general with shifting of the circle:
Tangent line: y=m*x+b
Normal line with m=-1/m <= m of tangent line
f(x):=a/b*sqrt(b^2+x^2)
f'(x):=a*x/(b*sqrt(b^2+x^2))
j=:x0
n(x)=-1/f'(t)*(x-t)+f(t) // general normal line equation
n(x,t)=-1/(a*t/(b*sqrt(b^2+t^2)))*(x-t)+a/b*sqrt(b^2+t^2)
= sqrt(b^2+t^2)*(a/b-(b*(x-t))/(a*t))
= (sqrt(b^2+t^2)*(a^2*t+b^2*(t-x)))/(a*b*t)
=-b*x*sqrt(b^2+t^2)/(a*t) + a*sqrt(b^2+t^2)/b + b*sqrt(b^2+t^2)/a
q=:A1 // q=0 => circlecenter on y-axis
t=:C1
n(q,t)=-b*q*sqrt(b^2+t^2)/(a*t) + a*sqrt(b^2+t^2)/b + b*sqrt(b^2+t^2)/a
n(t,t)=a/b*sqrt(b^2+t^2)=f(t)
t²+(n(q,t)-n(t,t))² = r² // pythagoras
<=>
r(q,t)=sqrt(t²+(n(q,t)-n(t,t))²)
r(q,t)=sqrt(t²+(-b*q*sqrt(b^2+t^2)/(a*t) + a*sqrt(b^2+t^2)/b + b*sqrt(b^2+t^2)/a-a*sqrt(b^2+t^2)/b)²)
=sqrt((a^2*t^4+b^4*(t-q)^2+b^2*t^2*(t-q)^2)/(a^2*t^2))
=sqrt(a^2*t^4+b^4*(t-q)^2+b^2*t^2*(t-q)^2)/(a*t) // a,b,q,t positive
t(r,q) = four long equations. taking the last where everything goes in positive:
t(r,q) = (q*b^2)/(2*(a^2+b^2))+1/2*sqrt((q^2*b^4)/(a^2+b^2)^2-(2*(b^4+q^2*b^2-a^2*r^2))/(3*(a^2+b^2))+(108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3+sqrt((108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3)^2-4*(-12*q^2*b^6+12*(a^2+b^2)*q^2*b^4+(b^4+q^2*b^2-a^2*r^2)^2)^3))^(1/3)/(3*2^(1/3)*(a^2+b^2))+(2^(1/3)*(-12*q^2*b^6+12*(a^2+b^2)*q^2*b^4+(b^4+q^2*b^2-a^2*r^2)^2))/(3*(a^2+b^2)*(108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3+sqrt((108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3)^2-4*(-12*q^2*b^6+12*(a^2+b^2)*q^2*b^4+(b^4+q^2*b^2-a^2*r^2)^2)^3))^(1/3)))+1/2*sqrt((2*q^2*b^4)/(a^2+b^2)^2-(4*(b^4+q^2*b^2-a^2*r^2))/(3*(a^2+b^2))-(108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3+sqrt((108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3)^2-4*(-12*q^2*b^6+12*(a^2+b^2)*q^2*b^4+(b^4+q^2*b^2-a^2*r^2)^2)^3))^(1/3)/(3*2^(1/3)*(a^2+b^2))-(2^(1/3)*(-12*q^2*b^6+12*(a^2+b^2)*q^2*b^4+(b^4+q^2*b^2-a^2*r^2)^2))/(3*(a^2+b^2)*(108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3+sqrt((108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3)^2-4*(-12*q^2*b^6+12*(a^2+b^2)*q^2*b^4+(b^4+q^2*b^2-a^2*r^2)^2)^3))^(1/3))+((8*q^3*b^6)/(a^2+b^2)^3+(16*q*b^4)/(a^2+b^2)-(8*q*(b^4+q^2*b^2-a^2*r^2)*b^2)/(a^2+b^2)^2)/(4*sqrt((q^2*b^4)/(a^2+b^2)^2-(2*(b^4+q^2*b^2-a^2*r^2))/(3*(a^2+b^2))+(108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3+sqrt((108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3)^2-4*(-12*q^2*b^6+12*(a^2+b^2)*q^2*b^4+(b^4+q^2*b^2-a^2*r^2)^2)^3))^(1/3)/(3*2^(1/3)*(a^2+b^2))+(2^(1/3)*(-12*q^2*b^6+12*(a^2+b^2)*q^2*b^4+(b^4+q^2*b^2-a^2*r^2)^2))/(3*(a^2+b^2)*(108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3+sqrt((108*q^4*b^8+108*(a^2+b^2)*q^2*b^8-36*q^2*(b^4+q^2*b^2-a^2*r^2)*b^6-72*(a^2+b^2)*q^2*(b^4+q^2*b^2-a^2*r^2)*b^4+2*(b^4+q^2*b^2-a^2*r^2)^3)^2-4*(-12*q^2*b^6+12*(a^2+b^2)*q^2*b^4+(b^4+q^2*b^2-a^2*r^2)^2)^3))^(1/3)))))
n(x,t(r,q)) should give the y-value of the circlecenter on x=q
n(x,t(r,q)), a=6, b=3, q=0, r=sqrt(89)/2 and wxMaxima says "division by zero" :-(
What it seems to say is that i should use the approximate procedure, when there is circleshifting
and the exact procedure if the center of the circle lies on the y-axis. So I was not that wrong.
Last edited by mathdrop (2022-11-22 18:49:32)
Offline
Pages: 1