Math Is Fun Forum

mathdrop

Member

Registered: 2022-03-07

Posts: 75

Circle in an angle

This is supposed to be a simpler 2D version
of a ball/torus resting in the tip of a pyramid.

It is about a circle resting in an angle.

Relative to the corner of the angle:
Where is the center of the Circle ?
Where does the Circle touch the angle ?

Bob

Administrator

Registered: 2010-06-20

Posts: 10,619

Re: Circle in an angle

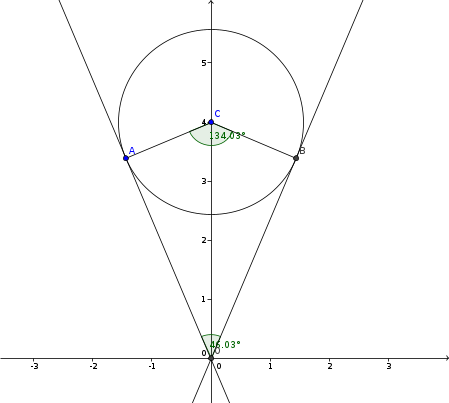
Let O be the vertex of the cone; C the centre of the circle and A be the point of contact.

OA will be a tangent so angle CAO is 90. Angle AOC is half the angle of the cone.

If you know AC then you can use trig to find OC.

Bob

---

Children are not defined by school ...........The Fonz
You cannot teach a man anything;  you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you!  …………….Bob

mathdrop

Member

Registered: 2022-03-07

Posts: 75

Re: Circle in an angle

This time we seem to have more or less the same approach.

You took O for origin, C for center and A for angle ?

The basic trigonometry formulas:
sin(alpha)=opposite/hypotenuse
cos(alpha)=adjacent/hypotenuse
tan(alpha)=opposite/adjacent
cot(alpha)=adjacent/opposite

(cause of the numerator/denominator flip
the 4th is not very worn out.)

In Germany, we often remember this
with somewhat funny abbreviations.

GAGA (=> crazy)
--------- (fraction line)
HHAG (Hummel Hummel AG => working like a bee, working like a bee - semi-public enterprise)

G => opposite.
A => adjacent
H => hypotenuse

With this you have those fractions after the equal sign.
The order sine, cosine, tangent cotangent needs to be
remembered by rote learning, here.

How is it being done in the UK ?

Now the trigonometry:

O->C:
sin(a)=G/H
H=G/sin(a)
H=r/sin(a/2)

O->A:
tan(a)=G/A
A=G/tan(a)
A=r/tan(a/2)

Edit: Correcting mistake.

Last edited by mathdrop (2022-11-03 16:09:11)