Math Is Fun Forum

lijon

Member

Registered: 2010-02-11

Posts: 4

Urgent: Help on calculus pyramid question

The problem I'm trying to solve:

In this problem you are asked to find the volume of a height h pyramid with a square base of width
w. (This is related to the Cheops pyramid problem, but we will use calculus.) Let the variable z
stand for distance down the axis of the pyramid with z = 0 at the top, and consider “slicing” the
pyramid along this axis (into horizontal slices). This will produce square “slices” (having area A(z)
and some width delta z). Calculate the volume of the pyramid as an integral by figuring out how A(z)
depends on z and integrating this function.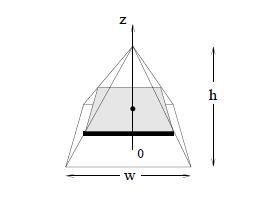

I have no idea where to even begin!
Any help is greatly appreciated

TheDude

Member

Registered: 2007-10-23

Posts: 361

Re: Urgent: Help on calculus pyramid question

What you're really interested in is the length of a side of the pyramid at height z, since A(z) is just that number squared.  Let's call this length L(z), and note that it is simply a linear function.  You have L(0) = 0 and L(h) = w, so L(z) = zw/h, giving us A(z) = (zw/h)^2.  Integrate this over 0 to h and you get your answer.

---

Wrap it in bacon

lijon

Member

Registered: 2010-02-11

Posts: 4

Re: Urgent: Help on calculus pyramid question

Simple and easy to understand explanation~ You were a great help. Thanks!