Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2011-02-09 09:50:34
- priyankshah
- Member
- Registered: 2011-02-08
- Posts: 5
Big O notation
hello everybody,
How can i prove by definition of big O that 2^n = O (n!).
thanks for help
Last edited by priyankshah (2011-02-09 10:00:19)
Offline
#2 2011-02-09 10:00:43
- priyankshah
- Member
- Registered: 2011-02-08
- Posts: 5
Re: Big O notation
Should i solve it by induction
Last edited by priyankshah (2011-02-09 10:10:36)
Offline
#3 2011-02-09 11:35:39
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Big O notation
Hi;
Why not use the definition of big O. If there exist c1 and c2 such that
f(n) ≤ c1 * g(n) when n> c2 then f(n) is O(g(n))
For yours why not c1 = 1 and c2 = 4.
2^n < n! when n > 4 so
2^n is O(n!)
Download this:
http://www.cs.utexas.edu/users/tandy/big-oh.pdf
If I got this right then please understand that Landau notation is all about definitions, that is why I hate it so much. Please brush up on yours by covering the first paragraph of the pdf.
Welcome to the forum.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#4 2011-02-09 17:34:18
- priyankshah
- Member
- Registered: 2011-02-08
- Posts: 5
Re: Big O notation
thanks for help i did it by induction and used limit formula of big O
lim n ->infinity f(x)/g(x) = 0
Offline
#5 2011-02-09 18:23:18
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Big O notation
Hi;
lim n ->infinity f(x)/g(x) = 0
You mean lim n ->infinity f(n)/g(n) = 0 Which is certainly true.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#6 2011-02-09 19:15:47
- gAr
- Member

- Registered: 2011-01-09
- Posts: 3,482
Re: Big O notation
Hi,
lim n ->infinity f(x)/g(x) = 0
Isn't that definition used for little-o?
"Believe nothing, no matter where you read it, or who said it, no matter if I have said it, unless it agrees with your own reason and your own common sense" - Buddha?
"Data! Data! Data!" he cried impatiently. "I can't make bricks without clay."
Offline
#7 2011-02-09 19:26:29
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Big O notation
Hi gAr;
Yes you are right, I did not notice that was incorrect too. His question read, prove it by the definition which I did in post #3.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#8 2011-02-09 19:53:40
- gAr
- Member

- Registered: 2011-01-09
- Posts: 3,482
Re: Big O notation
Hi bobbym,
I read your post #3, which is correct indeed. I just wanted to inform about the definition.
"Believe nothing, no matter where you read it, or who said it, no matter if I have said it, unless it agrees with your own reason and your own common sense" - Buddha?
"Data! Data! Data!" he cried impatiently. "I can't make bricks without clay."
Offline
#9 2011-02-10 02:46:17
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Big O notation
Hi gAr;
It is okay, you did the right thing. I got caught up in the fact that the OP used n and then x and forgot the other error. Thanks for pointing that out.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#10 2012-04-14 03:02:44
- cadmanapp
- Member
- Registered: 2012-04-14
- Posts: 3
Re: Big O notation
Can someone help me answer the following questions:
1. Is 2^(n+1)=O(2^n) ?
2. Is 2^(2n) = O(2^n)?
Offline
#11 2012-04-14 05:02:24
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Big O notation
Hi;
1. Is 2^(n+1)=O(2^n)
Now you can drop the constant 2. So I would say yes.
Or using the formal definition, we say
f(n) = O(g(n)) when
0 ≤ f(n) ≤ c g(n) when n > k and c and k are positive constants. So isn't
therefore
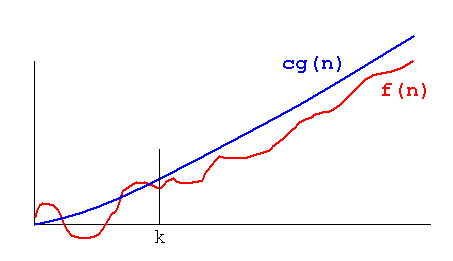
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#12 2012-04-14 05:31:34
- cadmanapp
- Member
- Registered: 2012-04-14
- Posts: 3
Re: Big O notation
Thank you for the response. Your response confirm what I did.
Can you help with the second question?
Offline
#13 2012-04-14 05:41:13
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Big O notation
Hi cadmanapp;
This is the way I think about it. 2^(2n) = (2^n)(2^n). For this to be big O to 2^n there would need to be some constant c that would always be greater than 2^n for all n. The graph of a constant is a horizontal line. 2^n will always surpass it for some n. Therefore I would say it is not big O to 2^n.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#14 2012-04-14 10:54:49
- cadmanapp
- Member
- Registered: 2012-04-14
- Posts: 3
Re: Big O notation
Thank you very much. Your explanation makes sense.
Offline
#15 2012-04-14 16:02:16
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Big O notation
Hi cadmanapp;
Your welcome!
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
Pages: 1