Graphing implicit polar equation?

benice · 2011-07-04 16:48:25

Hi All,

Could you please tell me what software can plot implicit polar equations?

Thanks!

bobbym · 2011-07-04 17:11:45

Hi benice;

Do you have an example?

benice · 2011-07-05 11:43:19

Hi bobbym,

Thanks for your reply!
Please see the Equation Grapher examples with x & y replaced by r & t.
My purpose is to make art with implicit polar equations, not to solve a specific math problem.

It is better if the software can also plot inequalities of the following types:
f(r,t) > 0, f(r,t) >= 0, f(r,t) < 0, f(r,t) <= 0.

Someone recommended me Mathematica. But it's too expensive!.

bobbym · 2011-07-05 15:03:14

Hi benice;

examples with x & y replaced by r & t.

Not to confuse you but polar coordinates are not quite the same as replacing the rectangular coordinates x, y with r and t.

My purpose is to make art with implicit polar equations, not to solve a specific math problem.

In mathematics the terms polar and implicit have an exact meaning which is very likely different than what you mean. That is why I asked to see an equation you are trying to graph.

You are talking about art and I, hopefully about mathematics. We must speak the same language. You might be able to get away with just an implicit plotter.

Someone recommended me Mathematica. But it's too expensive!

Are you a student? If so the price is drastically reduced. There are freeware alternatives but like mathematica they can overwhelming if you are just a casual user.

I have been to your page and some of that looks to me like it could be done by an implicit rectangular plotter. There is one over here.

If you are using polar coordiantes I could do a transformation to rectangular coordinates then any old plotter could do them.

benice · 2011-07-06 21:19:33

Hi bobbym,

Thanks for your kind reply!

Below is an example function
f(r,t) = sin(mr)*cos(nt - pi) - (3/4)*cos(kt - pi/2) - r³ + 3r - 3/4.

The plotter I use to experiment is Graph 4.3. It transforms the coordinates and then
plots implicit rectangular equations. The plotter works fine if n, k are integers or
rational numbers with small denominators.

The plotting speed is very slow if n, k are irrational numbers or rational numbers
with large denominators (e.g. k = 3/128). And this is why I am looking for a plotter
which can plot implicit polar equations directly and quickly.

m=8, n=6, k=5: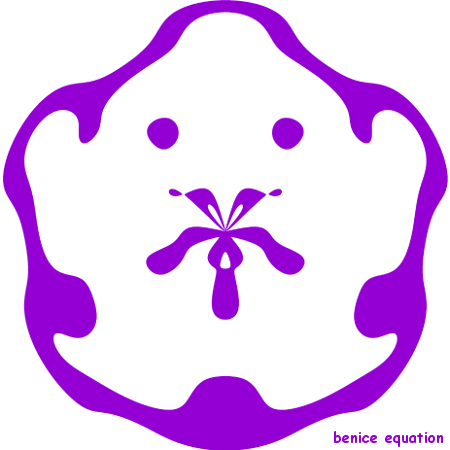

m=8, n=6, k=6:

bobbym · 2011-07-07 01:58:11

Hi;

For the first one:

m=8, n=6, k=5:

What intervals do you use for r and t?

benice · 2011-07-08 10:38:01

Hi bobbym,

I use the interval [-2,2] for both x and y, not for r and t.

bobbym · 2011-07-08 15:40:28

Hi benice;

I have been able to plot those functions with just an implict grapher in rectangular coordinates ( x, y ). You will no longer need a polar plotter. This might speed things up a bit.

The strange thing is your two graphs seem backwards. The bottom one is for m=8, n=6, k=5. And the top one is for m=8, n=6, k=6.

benice · 2011-07-08 16:55:16

bobbym wrote:

The strange thing is your two graphs seem backwards. The bottom one is for m=8, n=6, k=5. And the top one is for m=8, n=6, k=6.

Sorry! The equation should be
f(r,t) = sin(mr)*cos(nt - pi) + (3/4)*cos(kt - pi/2) - r³ + 3r - 3/4,
not
f(r,t) = sin(mr)*cos(nt - pi) - (3/4)*cos(kt - pi/2) - r³ + 3r - 3/4.

Last edited by benice (2011-07-08 20:12:32)

bobbym · 2011-07-08 20:16:00

Hi

Oh no! I did not see your edit when I did this post here. I will rework the problem with the new equation.

benice · 2011-07-08 21:43:48

Hi bobbym,

Here is what I use in the plotting process.

Define the following functions:

f0(x,y) = f( sqrt(x^2 + y^2), atan2(x,y) )
f1(x,y) = f( sqrt(x^2 + y^2), atan2(x,y) + 2*pi )
f2(x,y) = f( sqrt(x^2 + y^2), atan2(x,y) + 4*pi )
f3(x,y) = f( sqrt(x^2 + y^2), atan2(x,y) + 6*pi )
. . . . . .

g0(x,y) = f( -sqrt(x^2 + y^2), atan2(x,y) + pi )
g1(x,y) = f( -sqrt(x^2 + y^2), atan2(x,y) + 3*pi )
g2(x,y) = f( -sqrt(x^2 + y^2), atan2(x,y) + 5*pi )
g3(x,y) = f( -sqrt(x^2 + y^2), atan2(x,y) + 7*pi )
. . . . . .

Examples of plotting f(r,t) = 0:

m=8, n=6, k=5:
Plot f0(x,y) = 0, g0(x,y) = 0.

m=8, n=6, k=2.5:
Plot f0(x,y) = 0, f1(x,y) = 0, g0(x,y) = 0, g1(x,y) = 0.

m=8, n=6, k=1.25:
Plot f0(x,y) = 0, f1(x,y) = 0, f2(x,y) = 0, f3(x,y)=0,
and g0(x,y) = 0, g1(x,y) = 0, g2(x,y) = 0, g3(x,y) = 0.

Last edited by benice (2011-07-08 21:52:25)

bobbym · 2011-07-08 22:08:37

Hi;

I have some questions for later on your last post but for now would you plot this on your grapher.

benice · 2011-07-09 00:22:48

Hi bobbym,

-(x^2 + y^2)^(1.5) + 3*sqrt(x^2+y^2) - sin(8*sqrt(x^2+y^2))*cos(6*atan(y/x))
+ 0.75*sin(6*atan(y/x)) - 0.75 = 0

bobbym · 2011-07-09 04:36:25

Hi;

Regarding your post #11. It looks like you are already changing from polar to rectagular, which is what I am doing.

Why do you need all those equations. Mine is one equation. Why did you choose the atan2 command?

benice · 2011-07-09 11:49:41

bobbym wrote:

Why do you need all those equations. Mine is one equation.

Because the polar coordinate representation of a given point in the plane is not unique:
(r, t) = (r, t ± 2n*pi) = (-r, t ± (2n+1)*pi), where n is any integer.
I define f0, f1, f2, ... for (r, t ± 2n*pi) and g0, g1, g2, ... for (-r, t ± (2n+1)*pi).

bobbym wrote:

Why did you choose the atan2 command?

My idea came from this page. (See the section on 'Converting between polar and Cartesian coordinates'.)

bobbym · 2011-07-09 12:28:12

Hi benice;

Thanks for your patience. I did not think about the lack of uniqueness with the polar coordinates although it seems obvious now. But since you are using atan2 already why not restrict the interval you are graphing to be [ - π / 2 , π/2 ] instead of [-2,2]? Then the problem on non uniqueness disappears.

Let's say you can not do that, then are you saying that you graph all those functions for each drawing?

benice · 2011-07-09 16:17:00

Hi bobbym,
Thanks again for your reply.

bobbym wrote:

Let's say you can not do that, ...

Yes, I can't do that. Graph 4.3 does not support script. It plots equations of the type F(x,y) = 0 with variables x and y (not r and t).

bobbym wrote:

... , then are you saying that you graph all those functions for each drawing?

I graph those functions one at a time.
Please see the attached images plot_1.png ~ plot_4.png for the case m=8, n=6 and k=2.5.

The image plot_5.png shows that the graph of f2(x,y)=0 coincides with the graph of f0(x,y)=0.
There is thus no need to plot f2, f3, ... and g2, g3, ... .

Last edited by benice (2011-07-09 16:26:13)

bobbym · 2011-07-09 16:29:52

Hi;

Okay, let me look at what you have shown me.

In the assignment here:

f3(x,y) = f( sqrt(x^2 + y^2), atan2(x,y) + 6*pi )

What is f(...) equal to?

gAr · 2011-07-10 20:47:35

Hi benice,

For the equations in #5, did you edit the image for k=5?
I'm not getting a symmetry like that.
Here are the images I plotted using sagemath.

Update: I used atan() command there, for atan2() I get the same as yours.(3rd and 5th images)
1st image is for k = 3/128.
All of them took almost the same time (about 9.35s, using atan2() command)

Using atan() command is a lot quicker and incorrect!

Last edited by gAr (2011-07-10 23:12:03)

benice · 2011-07-11 20:31:43

bobbym wrote:

In the assignment here:
f3(x,y) = f( sqrt(x^2 + y^2), atan2(x,y) + 6*pi )
What is f(...) equal to?

-π < atan2(x,y) <= π
5π < atan2(x,y) + 6π <= 7π
The set of polar coordinates A = { (r,t) | f(r,t) = 0 , r∈[0,∞) , t∈(5π,7π] }
is transformed to the set of rectangular coordinates B = { (x,y) | f3(x,y) = 0, x∈R, y∈R }.
That is, A and B represent the same figure (curve) in the plane.

benice · 2011-07-11 20:39:49

Hi gAr,

gAr wrote:

Here are the images I plotted using sagemath.

Could you tell me which package did you use to make these images? Is it Matplotlib?

gAr · 2011-07-11 20:45:09

Hi benice,

Yes, sagemath uses matplotlib.
http://wiki.sagemath.org/plot

But I have not tried matplotlib separately.

benice · 2011-07-11 21:24:56

gAr wrote:

Yes, sagemath uses matplotlib.
http://wiki.sagemath.org/plot.

Thanks for the link!

gAr · 2011-07-11 21:30:50

Hi benice,

Since sage doesn't have a windows installer,
someone has created a livecd: https://groups.google.com/group/sage-de … 709f252bf6

Matplotlib is very capable, but got some learning curve.

Math Is Fun Forum

#1 2011-07-04 16:48:25

Graphing implicit polar equation?

#2 2011-07-04 17:11:45

Re: Graphing implicit polar equation?

#3 2011-07-05 11:43:19

Re: Graphing implicit polar equation?

#4 2011-07-05 15:03:14

Re: Graphing implicit polar equation?

#5 2011-07-06 21:19:33

Re: Graphing implicit polar equation?

#6 2011-07-07 01:58:11

Re: Graphing implicit polar equation?

#7 2011-07-08 10:38:01

Re: Graphing implicit polar equation?

#8 2011-07-08 15:40:28

Re: Graphing implicit polar equation?

#9 2011-07-08 16:55:16

Re: Graphing implicit polar equation?

#10 2011-07-08 20:16:00

Re: Graphing implicit polar equation?

#11 2011-07-08 21:43:48

Re: Graphing implicit polar equation?

#12 2011-07-08 22:08:37

Re: Graphing implicit polar equation?

#13 2011-07-09 00:22:48

Re: Graphing implicit polar equation?

#14 2011-07-09 04:36:25

Re: Graphing implicit polar equation?

#15 2011-07-09 11:49:41

Re: Graphing implicit polar equation?

#16 2011-07-09 12:28:12

Re: Graphing implicit polar equation?

#17 2011-07-09 16:17:00

Re: Graphing implicit polar equation?

#18 2011-07-09 16:29:52

Re: Graphing implicit polar equation?

#19 2011-07-10 20:47:35

Re: Graphing implicit polar equation?

#20 2011-07-11 20:31:43

Re: Graphing implicit polar equation?

#21 2011-07-11 20:39:49

Re: Graphing implicit polar equation?

#22 2011-07-11 20:45:09

Re: Graphing implicit polar equation?

#23 2011-07-11 21:24:56

Re: Graphing implicit polar equation?

#24 2011-07-11 21:30:50

Re: Graphing implicit polar equation?

Board footer