Circumscribed triangle!!!

anonimnystefy · 2012-04-03 10:57:10

Hi guys

I need help with this problem:

Given an arbitrary triangle find the equilateral triangle circumscribed around the original one such that the area of that equilateral triangle is maximized.

Can anyone help?

Bob · 2012-04-03 19:12:02

hi Stefy,

Not sure what you are after. Explain "circumscribed around".

Bob

also, what was your solution to the other triangle problem?

anonimnystefy · 2012-04-04 01:06:59

hi bob

It means that every vertex of the original triangle is on one different edge of the equilateral triangle.

As for the other problem-you need to draw three parallel line through P and then watch the smaller triangles.

bobbym · 2012-04-04 01:24:54

Supposing you have a 3,4,5 right triangle. How do you get an equilateral triangle cicumscribed around that?

anonimnystefy · 2012-04-04 02:08:14

hi bobbym

I am attaching a pic.On it you should see the given triangle ABC and the circumscribed triangle PQR.

bobbym · 2012-04-04 05:09:32

Hi;

I know of two possible ways to get this answer but neither of them is simple.

anonimnystefy · 2012-04-04 05:14:07

Nevermind,post away!

Btw,I recently took a look at that completing the cubes thread and that method is cool,but very complex,especially for remembering!

bobbym · 2012-04-04 05:17:59

1)There is a theorem that says about forming the largest altitude of the equilateral triangle.

2)Nonlinear programming.

anonimnystefy · 2012-04-04 05:23:45

We will go with the first one.What's the theorem?

bobbym · 2012-04-04 05:27:46

Here is something else which will help more.

1)Find the Fermat point of the interior triangle.

2)The antipedal triangle of that Fermat point is the equilateral triangle of maximum area that circumscribes the smaller interior triangle.

Theorem:If the inscribed triangle has area A, then the circumscribed triangle has areo of no more than 2A.

bobbym · 2012-04-04 05:33:01

The completing the cube method is total garbage and is typical of the type of math I hate!

anonimnystefy · 2012-04-04 05:46:16

hi bobbym

Can you prove:

2)The antipedal triangle of that Fermat point is the equilateral triangle of maximum area that circumscribes the smaller interior triangle.

bobbym · 2012-04-04 05:49:11

Hi;

No I can not. At this point I am not even sure what an antipedal triangle is. This is supposed to be proven already.

anonimnystefy · 2012-04-04 05:58:22

hi bobbym

Antipedal Triangle

bobbym · 2012-04-04 06:02:26

Yes, I know. If you use the Fermat point the antipedal triangle will circumscribe the interior triangle and be equilateral.

anonimnystefy · 2012-04-04 06:18:14

But why will it be maximum?

bobbym · 2012-04-04 06:21:50

Right now, I do not know. But it will have the biggest altitude and how many equilateral triangles like that are possible?

hammana · 2012-04-04 07:54:32

Hi bobbeam

This hint may help:
If we build three equilateral triangles on sides AB, BC , CA, and the three circles circumscribed to these tiangles, the vertexes of any equilateral triangle circumscribed to ABC should lie on these circles. The problem becomes the following: If M is an intersection of any 2 circles, a line passing by M intersects thes circles in 2 points, P and Q. How to choose this line to maximize PQ

bobbym · 2012-04-04 08:03:32

Hi hammana;

I am looking at that too, I do not know the best way yet.

anonimnystefy · 2012-04-04 08:07:00

hi bobbym

I figured that as well,but it looks hard.I will try to prove what you posted.

bobbym · 2012-04-04 08:30:31

Hi;

See you a little later will be busy for awhile.

anonimnystefy · 2012-04-04 10:24:16

Hi bobbym

We could prove the equivalent problem:

Given two intersecting circles,which have common points A and B,prove that the largest line that has one point on the first and second point on the second circle and goes through A is perpendicular to AB.

bobbym · 2012-04-04 10:31:25

I am not following you but if you can see your way through with it then go ahead.

I am halfway through the Fermi point and whatever that triangle is called.

anonimnystefy · 2012-04-04 10:41:28

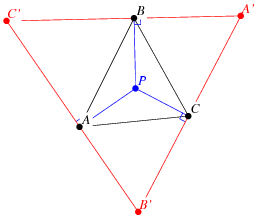
hi bobbym

See the attached pic.

bobbym · 2012-04-04 18:37:49

Hi;

Still am not following how that is going to answer the question.

Math Is Fun Forum

#1 2012-04-03 10:57:10

Circumscribed triangle!!!

#2 2012-04-03 19:12:02

Re: Circumscribed triangle!!!

#3 2012-04-04 01:06:59

Re: Circumscribed triangle!!!

#4 2012-04-04 01:24:54

Re: Circumscribed triangle!!!

#5 2012-04-04 02:08:14

Re: Circumscribed triangle!!!

#6 2012-04-04 05:09:32

Re: Circumscribed triangle!!!

#7 2012-04-04 05:14:07

Re: Circumscribed triangle!!!

#8 2012-04-04 05:17:59

Re: Circumscribed triangle!!!

#9 2012-04-04 05:23:45

Re: Circumscribed triangle!!!

#10 2012-04-04 05:27:46

Re: Circumscribed triangle!!!

#11 2012-04-04 05:33:01

Re: Circumscribed triangle!!!

#12 2012-04-04 05:46:16

Re: Circumscribed triangle!!!

#13 2012-04-04 05:49:11

Re: Circumscribed triangle!!!

#14 2012-04-04 05:58:22

Re: Circumscribed triangle!!!

#15 2012-04-04 06:02:26

Re: Circumscribed triangle!!!

#16 2012-04-04 06:18:14

Re: Circumscribed triangle!!!

#17 2012-04-04 06:21:50

Re: Circumscribed triangle!!!

#18 2012-04-04 07:54:32

Re: Circumscribed triangle!!!

#19 2012-04-04 08:03:32

Re: Circumscribed triangle!!!

#20 2012-04-04 08:07:00

Re: Circumscribed triangle!!!

#21 2012-04-04 08:30:31

Re: Circumscribed triangle!!!

#22 2012-04-04 10:24:16

Re: Circumscribed triangle!!!

#23 2012-04-04 10:31:25

Re: Circumscribed triangle!!!

#24 2012-04-04 10:41:28

Re: Circumscribed triangle!!!

#25 2012-04-04 18:37:49

Re: Circumscribed triangle!!!

Board footer