Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2012-05-31 02:39:10
- jimi70
- Member
- Registered: 2012-04-04
- Posts: 22
Vector geometry
I came across this problem the other day. I understand the vectors behind it but don't really have a definite strategy in solving it. My approach is a bit random. Can someone please advise me of the best way to approach it?
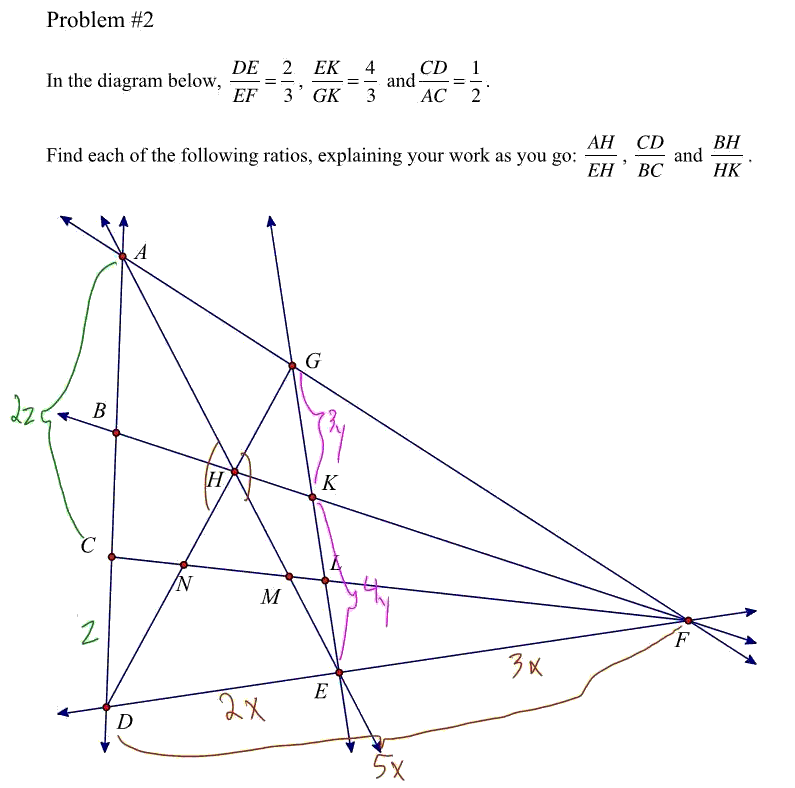
Offline
#2 2012-05-31 02:48:41
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,811
Re: Vector geometry
hi jimi70
I would do this one like the last.
Choose two non parallel vectors to form the basis for all the rest.
looking at the problem and the information I'd have FD = d and FA = a
As before you can write everything else in terms of a and d.
Start with
AC = ?
CD = ?
FE = ?
FG = ? This one looks tricky because you haven't been told how far G is along FA. So let FG = gFA and the value of g should come out later.
EG = ?
EK = ?
DG = ?
Now you can find H.
Bob
EA = ?
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#3 2012-06-02 10:19:07
- jimi70
- Member
- Registered: 2012-04-04
- Posts: 22
Re: Vector geometry
Hi bob
I got the following:
AC = 2/3(-a + d)
CD = 1/3(-a + d)
FE = 3d/5
FG = na
EG = -3d/5 + na
EK = 4/7(-3d/5 + na)
DG = -d + na
but I still don't know what to do next.
Offline
#4 2012-06-02 19:46:54
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,811
Re: Vector geometry
hi jimi70
This is the nastiest problem of this type that I have seen. The algebra gets horrid so you'll need to be careful.
One of my suggested vectors somehow got below my signature.
I agree with all the ones you have found.
Carry on by finding EA.
Now H is at the crossover of AE and DG.
So you can find FH two ways, which will give you a pair of simultaneous equations.
Write AH as 'lambda' AE and get FH that way.
Write GH as 'mu' GD and write FH that way.
But there are three unknowns, lambda, mu and n.
So another constraint is required.
I began to think that G is free to float along FA, so I thought I'd use my program Sketchpad to draw it out.
I marked points in this order: F, A, D, C, E. All these are determined by the given constraints.
Then I placed G anywhere along FA and continued with: K, B, H
At this point DH could be produced to cross FA at G.
See my diagram below. It didn't coincide with where I had put G.
So I moved G along until it met DH produced. G is then fixed.
So the extra constraint is that EG and DH meet at G.
So write DH = 'nu' DG and form two expressions for FG.
Setting them equal give two more equations, but only one new unknown, 'nu'.
So with all four equations you can find lambda, mu, nu and n.
That fixes everything and the questions are easy (huh! relatively!!).
There are variations by starting with different base vectors, but they'll all come up against the same intersection constraints so I don't think any other will be quicker or easier.
Hope you are good at simultaneous equations! ![]()
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#5 2012-06-06 09:22:28
- hammana
- Member
- Registered: 2012-03-02
- Posts: 48
Re: Vector geometry
Hi!
It seems to me that some data is missing, because I can draw a figure satisfying the conditions for DE/EF, EK/GK, CD/AC, with an arbitrary value for CD/BC.
Offline
#6 2012-06-06 11:44:31
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,811
Re: Vector geometry
hi hammana
Are you sure? This is a vector geometry problem not Euclidean.
You may change the base vectors, but the ratios are fixed.
Have a look at my two diagrams below.
In Sketchpad it is possible to build in the constraints (like E lies on CF)
All I did to get the second diagram was to move A and D. The ratios were unchanged.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
Pages: 1