amc problems

mathstudent2000 · 2013-10-25 11:41:55

1. A cube is sliced with one straight slice which passes through two opposite edges. The result is two solids, as shown. The area of the largest face on one of these two solids is 242\sqrt {2} square units. What was the exact surface area of the original cube?

2. A rectangle contains two circles of radius 6 that are each tangent to the rectangle in exactly 3 points. If the distance between the centers of the circles is 10, what is the area of the rectangle?

3. The rectangle below has height 8 and width 9. What value of k would make the shaded triangle's area 12\frac12% of the rectangle's area?

4. A 4" by 6" by 8" rectangular solid is cut by slicing through the midpoint of three adjacent edges. What is the number of inches in the sum of the lengths of the edges of the tetrahedron that is cut?

5. A cube of volume 27 has 1 x 1 square holes drilled through the center of each face and passing through the center of the cube. What is the volume of the figure that remains?

6. The circle is inscribed in a square with sides 8 cm. What is the area of the shaded part in square centimeters? Express your answer in terms of \pi.

bobbym · 2013-10-25 16:34:28

Hi;

5) I am getting that 7 1 x 1 cubes are removed so the resulting volume is 20

Where are the drawings? For instance #6, which area do you want?

mathstudent2000 · 2013-10-27 15:26:57

the picture is here: http://classroom.artofproblemsolving.com/latex/e/4/4/e44183c89cddb01c6e653eb0a08526a673fb8717.png

mathstudent2000 · 2013-10-27 15:30:16

got another question: The triangle ABC shown is a right triangle. The semicircles have the sides of the triangle as diameters. The areas of two of the semicircles are shown. What is the area of the third semicircle?

https://www.google.com/search?tbs=sbi:A … tDeOQ2gUs#

the image is the one in the search

bobbym · 2013-10-27 15:35:06

Hi;

That link gets me to google's front page?

Nehushtan · 2013-10-27 22:06:26

I get the following thumbnail but I cant open it on the Google page.

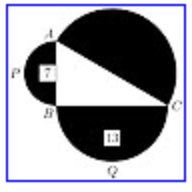
Use Pythagorass theorem and this formula:

where d is semicircle diameter / triangle side and A and is semicircle area. Thus

Hence the area of the third semicircle is 20.

mathstudent2000 · 2013-11-07 12:41:37

i'm pretty much sure it gets to the main pic

bobbym · 2013-11-07 13:26:11

Hi;

6) 32 pi - 32

Nehushtan · 2013-11-08 11:15:46

Monox D. I-Fly · 2019-07-29 15:26:43

mathstudent2000 wrote:

4. A 4" by 6" by 8" rectangular solid is cut by slicing through the midpoint of three adjacent edges. What is the number of inches in the sum of the lengths of the edges of the tetrahedron that is cut?

I got

. Am I doing this right?

Math Is Fun Forum

#1 2013-10-25 11:41:55

amc problems

#2 2013-10-25 16:34:28

Re: amc problems

#3 2013-10-27 15:26:57

Re: amc problems

#4 2013-10-27 15:30:16

Re: amc problems

#5 2013-10-27 15:35:06

Re: amc problems

#6 2013-10-27 22:06:26

Re: amc problems

#7 2013-11-07 12:41:37

Re: amc problems

#8 2013-11-07 13:26:11

Re: amc problems

#9 2013-11-08 11:15:46

Re: amc problems

#10 2019-07-29 15:26:43

Re: amc problems

Board footer