Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2014-03-06 04:25:30
- PHRU
- Member
- Registered: 2014-03-06
- Posts: 6
Golden Ratio Rectangle: 1/2 + √5/2
Hello,
I'm a beginner and would need help to understand the drawing of a rectangle based on the golden ratio:
Why is the length of one side 1/2 + √5/2 ?
Thanks a lot!
Offline
#2 2014-03-06 04:28:52
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Golden Ratio Rectangle: 1/2 + √5/2
Hi;
What part do you not understand? The construction?
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#3 2014-03-06 04:38:33
- PHRU
- Member
- Registered: 2014-03-06
- Posts: 6
Re: Golden Ratio Rectangle: 1/2 + √5/2
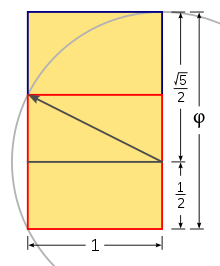
Yes, the construction - on mathsisfun.com (I cannot post the link) the step-by-step instructions are:
"Here is one way to draw a rectangle with the Golden Ratio:
Draw a square (of size "1")
Place a dot half way along one side
Draw a line from that point to an opposite corner (it will be √5/2 in length)
Turn that line so that it runs along the square's side
Then you can extend the square to be a rectangle with the Golden Ratio."
My question relates to the 3rd bullet point. Why is the line √5/2 in length?
Thanks!
Offline
#4 2014-03-06 04:39:56
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Golden Ratio Rectangle: 1/2 + √5/2

Do you see the line with the arrow head at the end? That is what is √ 5 / 2 and it is computed using the Pythagorean theorem.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#5 2014-03-06 04:41:53
- PHRU
- Member
- Registered: 2014-03-06
- Posts: 6
Re: Golden Ratio Rectangle: 1/2 + √5/2
Yes - I do not understand why it's √5/2 in length
Offline
#6 2014-03-06 04:42:59
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Golden Ratio Rectangle: 1/2 + √5/2
Do you see that it is the hypotenuse of a right triangle? Or do you need a better diagram?
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#7 2014-03-06 04:50:09
- PHRU
- Member
- Registered: 2014-03-06
- Posts: 6
Re: Golden Ratio Rectangle: 1/2 + √5/2
Yes, I see it:
so 1² + 1/2²=
1+1/4 = 5/4
√ 5/4 = √5/2 ?
Offline
#8 2014-03-06 04:53:04
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Golden Ratio Rectangle: 1/2 + √5/2
That is correct! That is using the Pythagorean theorem. That line segment is used to sweep out until it makes a rectangle with sides 1 and ( 1 / 2) + √ 5 / 2.
Everything better or more work needed?
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#9 2014-03-06 05:02:34
- PHRU
- Member
- Registered: 2014-03-06
- Posts: 6
Re: Golden Ratio Rectangle: 1/2 + √5/2
Great, thanks!
Offline
#10 2014-03-06 05:03:53
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Golden Ratio Rectangle: 1/2 + √5/2
You are welcome and welcome to the forum.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#11 2014-03-06 05:10:06
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,803
Re: Golden Ratio Rectangle: 1/2 + √5/2
hi PHRU,
Welcome to the forum.
This is how I've introduced this to classes in the past.
Start with a rectangle, say 4 x 1. Chop off a square ( 1x1 ) and you're left with a differently proportioned rectangle, 3 x 1
Start with a different rectangle, let's say 2 x 1. Chop off the 1 x 1 square and you're left with a rectangle 1 x 1. Again the proportion of length to width has changed ( from 2:1 into 1:1)
So, can you find a rectangle in a certain proportion, say x:1, so that when you cut off a square, what's left is still in the same ratio?
See diagram below.
The start rectangle is x by 1. After a square is removed, the rectangle that is left now has measurements 1 by (x-1). If these must be in the same ratio then
If you use the quadratic formula to solve this the larger root is
which is the golden ratio. The other root is the reciprocal of the golden ratio.
And if you start with that rectangle and chop off a square you get another rectangle in the ratio; and if you start with that rectangle ......... for ever. ![]()
That's why you get a neat spiral if you join up corresponding points in all the recatngles.
But how do snails know this?
http://io9.com/5985588/15-uncanny-examp … -in-nature
Bob
Last edited by Bob (2014-03-06 05:17:42)
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#12 2014-03-06 05:20:05
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Golden Ratio Rectangle: 1/2 + √5/2
Hi Phillip;
Here is the drawing that you can look at.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#13 2014-03-06 22:42:59
- PHRU
- Member
- Registered: 2014-03-06
- Posts: 6
Re: Golden Ratio Rectangle: 1/2 + √5/2
Thank you for all replies which were very helpful!
Do you maybe have also a short introduction on how to solve a quadratic equation?
hi PHRU,
Welcome to the forum.
This is how I've introduced this to classes in the past.
Start with a rectangle, say 4 x 1. Chop off a square ( 1x1 ) and you're left with a differently proportioned rectangle, 3 x 1
Start with a different rectangle, let's say 2 x 1. Chop off the 1 x 1 square and you're left with a rectangle 1 x 1. Again the proportion of length to width has changed ( from 2:1 into 1:1)
So, can you find a rectangle in a certain proportion, say x:1, so that when you cut off a square, what's left is still in the same ratio?
See diagram below.
The start rectangle is x by 1. After a square is removed, the rectangle that is left now has measurements 1 by (x-1). If these must be in the same ratio then
If you use the quadratic formula to solve this the larger root is
which is the golden ratio. The other root is the reciprocal of the golden ratio.
And if you start with that rectangle and chop off a square you get another rectangle in the ratio; and if you start with that rectangle ......... for ever.
That's why you get a neat spiral if you join up corresponding points in all the recatngles.
But how do snails know this?
Bob
Offline
#14 2014-03-06 23:38:44
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Golden Ratio Rectangle: 1/2 + √5/2
Hi;
http://www.mathsisfun.com/algebra/quadr … ation.html
When you have gone over that as best as you can we will do a few of them.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
Pages: 1