Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2014-10-23 00:56:52
- TeoLeo
- Member
- Registered: 2014-10-23
- Posts: 3
A question about limits
Ok guys, I can't work out this sequence limit:
lim sin( π√(4n^2+n) ) = ?
n⇒∞
I'm sure it's not really that hard, but...help, please!! ![]()
Offline
#2 2014-10-23 03:20:29
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: A question about limits
Hi;
I would say that limit does not exist.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#3 2014-10-23 03:20:59
- Olinguito
- Member

- Registered: 2014-08-12
- Posts: 649
Re: A question about limits
This is a tricky one. Consider
[list=*]
[*]
[/list]
Hence
[list=*]
[*]
[/list]
Last edited by Olinguito (2014-10-23 03:22:28)
Bassaricyon neblina
Offline
#4 2014-10-23 03:56:33
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: A question about limits
Hi;
Are you sure you are allowed to take the limit inside the sin() like that?
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#5 2014-10-23 04:11:24
- Olinguito
- Member

- Registered: 2014-08-12
- Posts: 649
Re: A question about limits
For continuous functions f, yes:
[list=*]
[*]
[/list]
In fact this is part of the definition of continuousness!
Bassaricyon neblina
Offline
#6 2014-10-23 04:17:09
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: A question about limits
Hi;
But this is not a continuous function. It says a sequence limit, implying a discrete function. I am not trying to be a nit, the experts agree with your answer. I am just trying to see if I can understand the question like you do. Thanks.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#7 2014-10-23 04:32:11
- Olinguito
- Member

- Registered: 2014-08-12
- Posts: 649
Re: A question about limits
But this is not a continuous function.
Of course the it is! It’s the sine function.
For any continuous function f, if then .
http://en.wikipedia.org/wiki/Limit_of_a … Properties
Last edited by Olinguito (2014-10-23 04:35:31)
Bassaricyon neblina
Offline
#8 2014-10-23 04:33:48
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: A question about limits
Hi;
Okay, thanks for the help.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#9 2014-10-23 04:57:30
- Olinguito
- Member

- Registered: 2014-08-12
- Posts: 649
Re: A question about limits
Here’s what I did on Excel:
[list=*]
[*]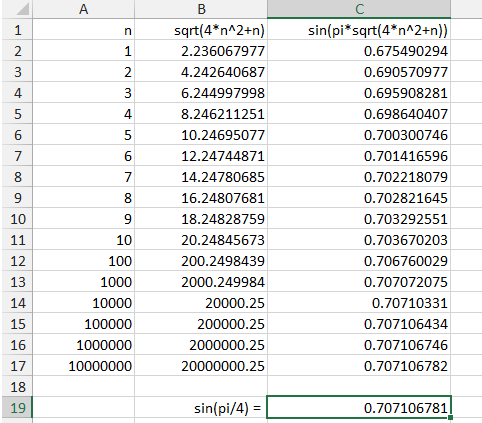 [/*]
[/*]
[/list]
Bassaricyon neblina
Offline
#10 2014-10-23 05:01:46
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: A question about limits
Hi;
Yes, that is true but notice that you also made the decision to treat n as an integer. If you did not then the limit would not exist.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#11 2014-10-23 05:10:40
- Olinguito
- Member

- Registered: 2014-08-12
- Posts: 649
Re: A question about limits
Hi;
Yes, that is true but notice that you also made the decision to treat n as an integer. If you did not then the limit would not exist.
I agree.
[list=*]
[*]
[/list]
definitely does not exist. But
[list=*]
[*]
[/list]
does – since in this case we ignore all values that are not the image of integer n.
Bassaricyon neblina
Offline
#12 2014-10-23 05:11:41
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: A question about limits
So why choose n as an integer?
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#13 2014-10-23 05:14:50
- Olinguito
- Member

- Registered: 2014-08-12
- Posts: 649
Re: A question about limits
Why not? We’re dealing with sequences here, aren’t we?
Last edited by Olinguito (2014-10-23 05:18:26)
Bassaricyon neblina
Offline
#14 2014-10-23 05:21:14
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: A question about limits
That is the answer. I did not see that and assumed a function limit.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#15 2014-10-23 05:28:12
- Olinguito
- Member

- Registered: 2014-08-12
- Posts: 649
Re: A question about limits
Let’s see what the OP says.
Bassaricyon neblina
Offline
#16 2014-10-23 07:28:12
- TeoLeo
- Member
- Registered: 2014-10-23
- Posts: 3
Re: A question about limits
Hi, Olinguito.
I don't really understand the first part with "Consider: √(4n^2+n) - 2n" .
What's with that 2n?
understand everything else after that...so is "-2n" added there just randomly to help us? Or why did you chooose it?
Last edited by TeoLeo (2014-10-23 07:45:06)
Offline
#17 2014-10-23 20:36:29
- Olinguito
- Member

- Registered: 2014-08-12
- Posts: 649
Re: A question about limits
Notice that
[list=*]
[*]
[/list]
That’s pretty useless to us. What we need is more than that: we need to show
[list=*]
[*]
[/list]
In order to do that we show
[list=*]
[*]
[/list]
Last edited by Olinguito (2014-10-23 20:42:43)
Bassaricyon neblina
Offline
Pages: 1