Math Is Fun Forum

renjer

Member

Registered: 2006-04-29

Posts: 50

Surface Integral Question

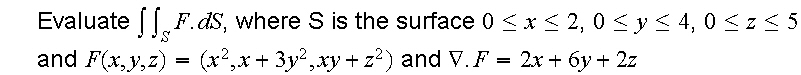
Thanks for the prompt reply of my other question today. Here's another one.
The problem with this one is that, the surface integral formula only has 2 variables in it, x and y. But this one has another z variable (the k term).

So how do I go about doing this? (I did grad . F already before this)

And no, I can't use the divergence theorem here because I'm supposed to prove it.

Ricky

Moderator

Registered: 2005-12-04

Posts: 3,791

Re: Surface Integral Question

What you are doing is integrating over the surfaces of a block.  So you can set up 6 different integrals, each with respect to two variables, and add them all together.

Ugly, but I think it will work.

Last edited by Ricky (2006-04-30 03:34:07)

---

"In the real world, this would be a problem.  But in mathematics, we can just define a place where this problem doesn't exist.  So we'll go ahead and do that now..."

renjer

Member

Registered: 2006-04-29

Posts: 50

Re: Surface Integral Question

What 6 integrals do I need to set up? I know these:
a) between the x and y (limits 2,0 and 4,0)
b) between x and z (limits 2,0 and 5,0)
c) between y and z (limits 4,0 and 5,0)

What are the other 3 integrals I need to set up?

George,Y

Member

Registered: 2006-03-12

Posts: 1,379

Re: Surface Integral Question

z=0, 0<x<2, 0<y<4
z=5, 0<x<2, 0<y<4
......

Last edited by George,Y (2006-05-03 02:52:52)

---

X'(y-Xβ)=0

renjer

Member

Registered: 2006-04-29

Posts: 50

Re: Surface Integral Question

Actually my lecturer told me to use a flux integral F.ndS. He talked about normal to the surface and something like that, eg the right most surface of the box has a positive j component. In that case I'd use dx and dz he says. But I still don't really understand this concept.  (by the way I can't ask him too much because this is an assignment question).

George, I tried your method, it seems like whether z=0 or z=5, it doesn't affect the equation at all because when I take the partials of x and y, the z part disappears.

Last edited by renjer (2006-05-05 19:57:50)

renjer

Member

Registered: 2006-04-29

Posts: 50

Re: Surface Integral Question

Anyone knows how to solve this problem?

Ricky

Moderator

Registered: 2005-12-04

Posts: 3,791

Re: Surface Integral Question

Sorry about the delay.  If you have trouble understanding any of this, let me know.  It's hard to do a complete explanation because there are a lot of things you probably understand, and I don't want to write a book if I don't have to .  Ok, so we have a cube with six sides:

Now we have the normals.  I'm going to assume we want outward facing normals, although I'm not entirely sure why that fact isn't given to you.

Finally, let:

So now:

Then we have:

Not quite sure why latex doesn't format that right, but at least it's readable.

After integrating all of these, I get 760.  Is that what you get doing the divergence thm?

---

"In the real world, this would be a problem.  But in mathematics, we can just define a place where this problem doesn't exist.  So we'll go ahead and do that now..."

renjer

Member

Registered: 2006-04-29

Posts: 50

Re: Surface Integral Question

Yes of course, using the divergence theorem is so much faster and easier too.

This is kind of complicated, but I'm getting what you're saying. How did you learn all this? Are you a maths genius?

Oh, and I was kind of worried that there was no answer since I have to hand in this assignment tomorrow.

Anyway, thanks for replying. It helped a lot.

Last edited by renjer (2006-05-07 03:30:28)