Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2015-04-09 10:12:25
- classof2020
- Member
- Registered: 2015-02-03
- Posts: 4
Geometry Problem
In the diagram below, we have XY = 2AX = 2YB and AZ/ZC = 2/3. Find the ratio of the area of triangle YBC to the area of triangle ZYC.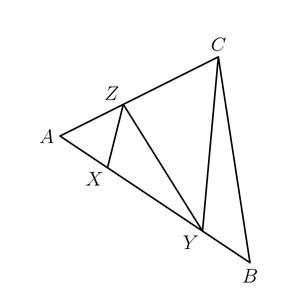
I think we could use similar triangles, but I'm not sure exactly where. Any help with this problem would be greatly appreciated. Thanks!
Offline
#2 2015-04-09 10:41:36
- jeff787
- Member
- Registered: 2015-04-08
- Posts: 7
Re: Geometry Problem
Use law of sines focusing on angle B. Actually, just use sines.
Last edited by jeff787 (2015-04-09 10:43:04)
Offline
#3 2015-04-09 10:54:04
- classof2020
- Member
- Registered: 2015-02-03
- Posts: 4
Re: Geometry Problem
Is there a way other than trigonometry? I haven't learned trig yet.
Offline
#4 2015-04-09 11:02:25
- jeff787
- Member
- Registered: 2015-04-08
- Posts: 7
Re: Geometry Problem
Basically, the sine is just a ratio of triangle side lengths which then stays the same for similar (right) triangles. Look at the areas of the triangles by drawing in the triangle heights making sure that the angle B is opposite the height. You should notice that same similar triangle reappears in several places in the figure.
Offline
#5 2015-04-09 19:29:26
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,811
Re: Geometry Problem
hi classof2020
As Jeff says, trig is the quick way to do this. But you can do it just using the area of a triangle formula (=0.5 x base x height)

In this diagram, I've introduced the lines ZU and CV, perpendicular to AB.
As they are both perpendicular => ZU is parallel to CV so AZU and ACV are similar triangles. => If ZU = 2h, then CV = 5h.
So, if you say AX = x, you can work out all these areas in terms of x and h:
AZX, AZY, AYC, ABC and hence the areas ZYC and YCB by subtraction.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#6 2015-04-10 01:34:21
- jeff787
- Member
- Registered: 2015-04-08
- Posts: 7
Re: Geometry Problem
I ended up seeing 3 different solutions to the problem, a fast, a medium, and a slow solution. The solution that Bob is pointing to is the medium one. The slow one is just a twisted (or flipped) version of that one. The fast one directly uses areas in units of the area of the large triangle, and for me can be done in my head without need of paper. It is sort of the "Ah Hah!" solution. I didn't see it until I put in the height from C, i.e. after the other solutions. The problem with that solution is giving a hint. It's a little like getting someone to see one those stereograms, you want to say "Well, you just gotta see it". Not too helpful. I think the key hint is still angle B although maybe stated in not quite as contorted fashion. I hope classof2020 wasn't too put off by my response and made a stab at it, and if he or she is still following, good luck in what I assume is your geometry class.
On a side issue, I've never considered the sine, etc to be purely circular functions, or trig functions as classof2020 put it. I was (as in way way back) introduced to them as geometry concepts relating to similar right triangles, and it always has felt right tieing (tying?) them to similar triangles early on. If one uses that standard diagram with two rays forming an angle and a sequence of parallel perpendiculars set out from one ray to the other, then it is visually obvious that those are a sequence of similar triangles and can be extended indefinitely. Consequently the ratio of two corresponding sides of any two triangles is constant and consequently constant for the figure as a whole. Then it's easy to see that there can be 6 constants (3 possible sides * 2 remaining sides) which gives the 6 functions or constants for that angle. However, I don't know if that's how they present it these days.
Last edited by jeff787 (2015-04-10 01:36:28)
Offline
Pages: 1